1
people have died from curable diseases
since this page started loading...
Abstract
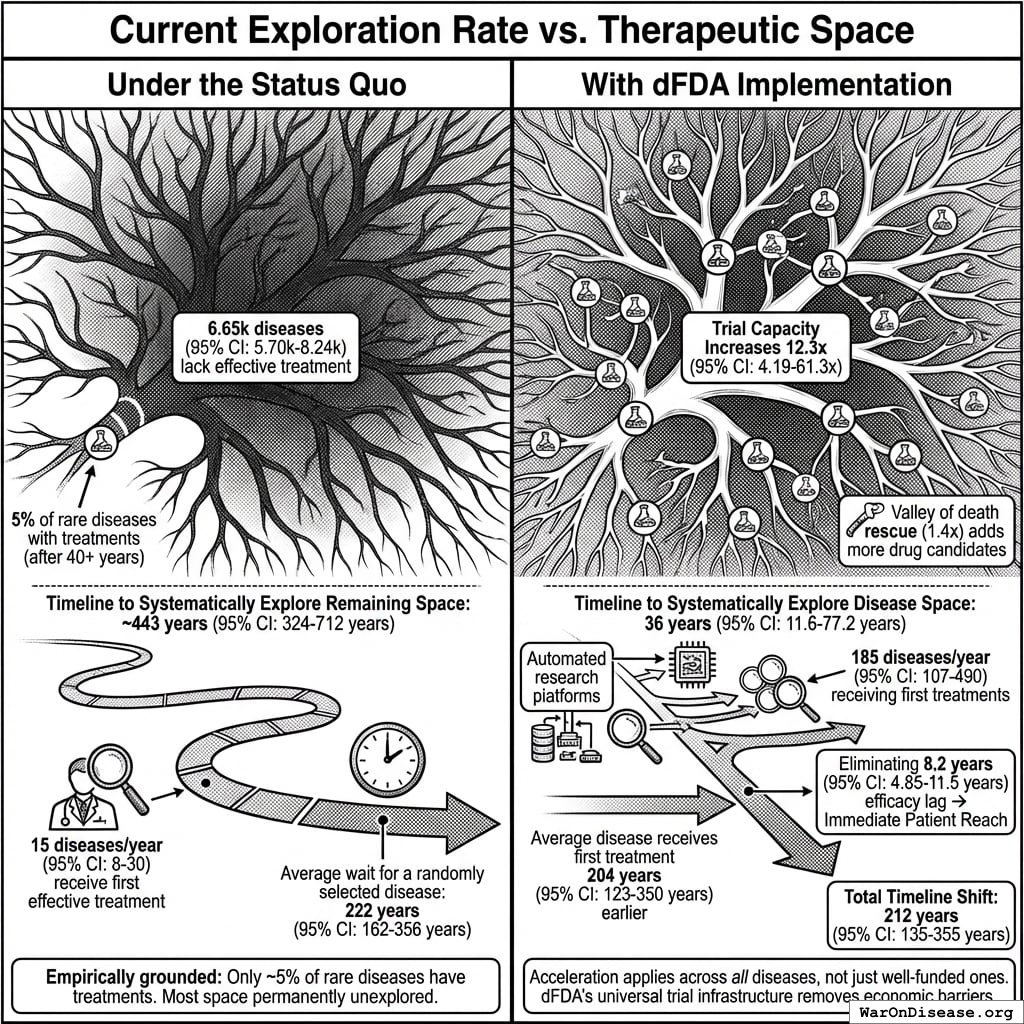
The bottleneck: Approximately 6.65 thousand diseases (95% CI: 5.70 thousand diseases-8.24 thousand diseases) have zero FDA-approved treatments. At current trial capacity (~15 diseases/year (95% CI: 8 diseases/year-30 diseases/year) new treatments/year), systematically testing all 9.50 million combinations plausible drug-disease combinations would take ~443 years (95% CI: 324 years-712 years). Effectively never.
\[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\]
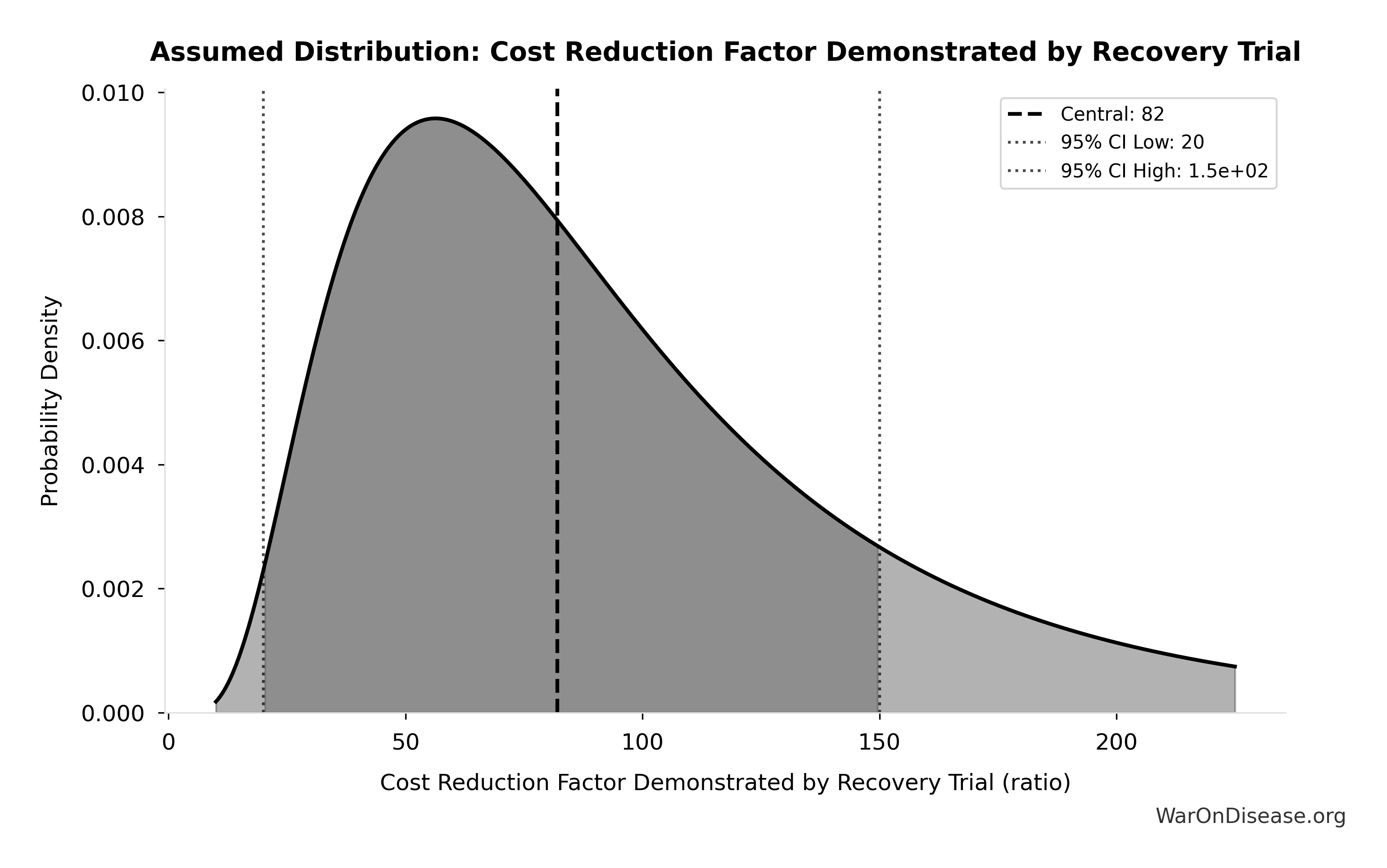
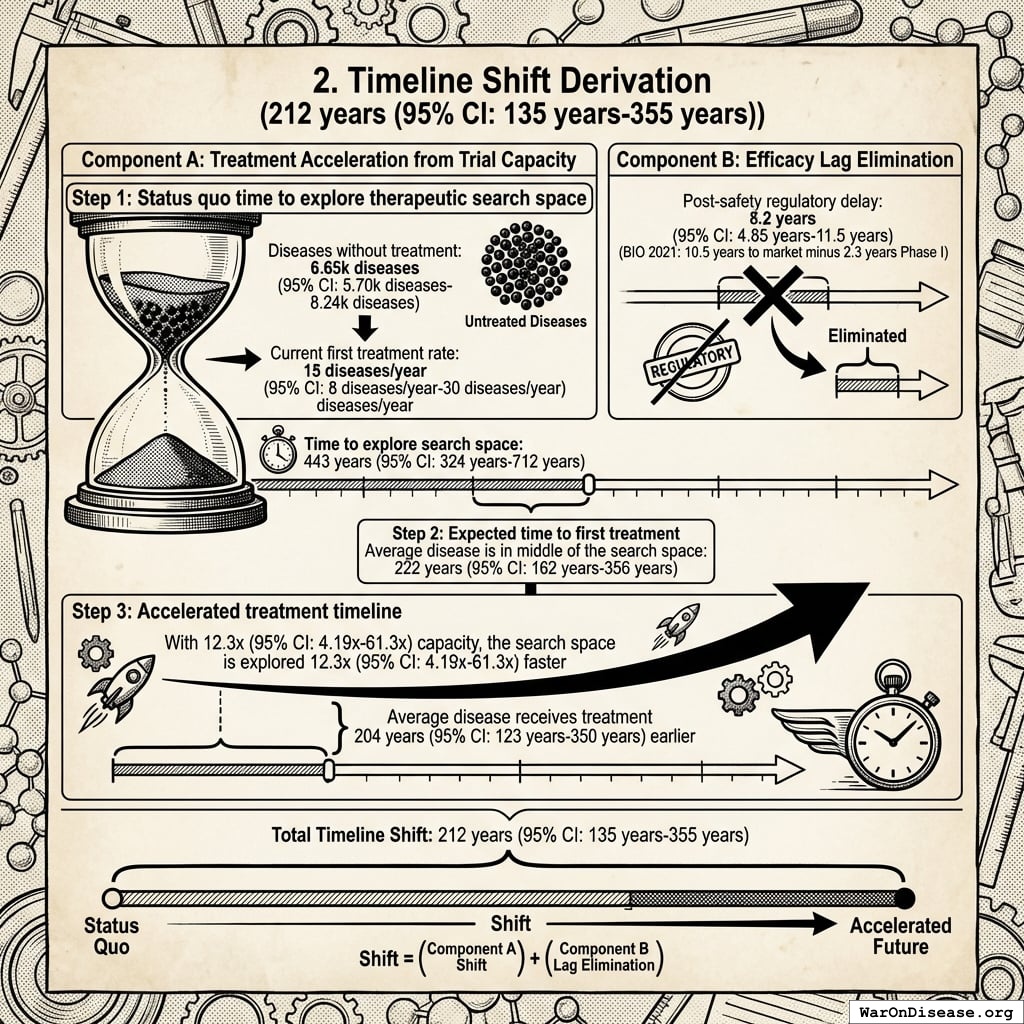
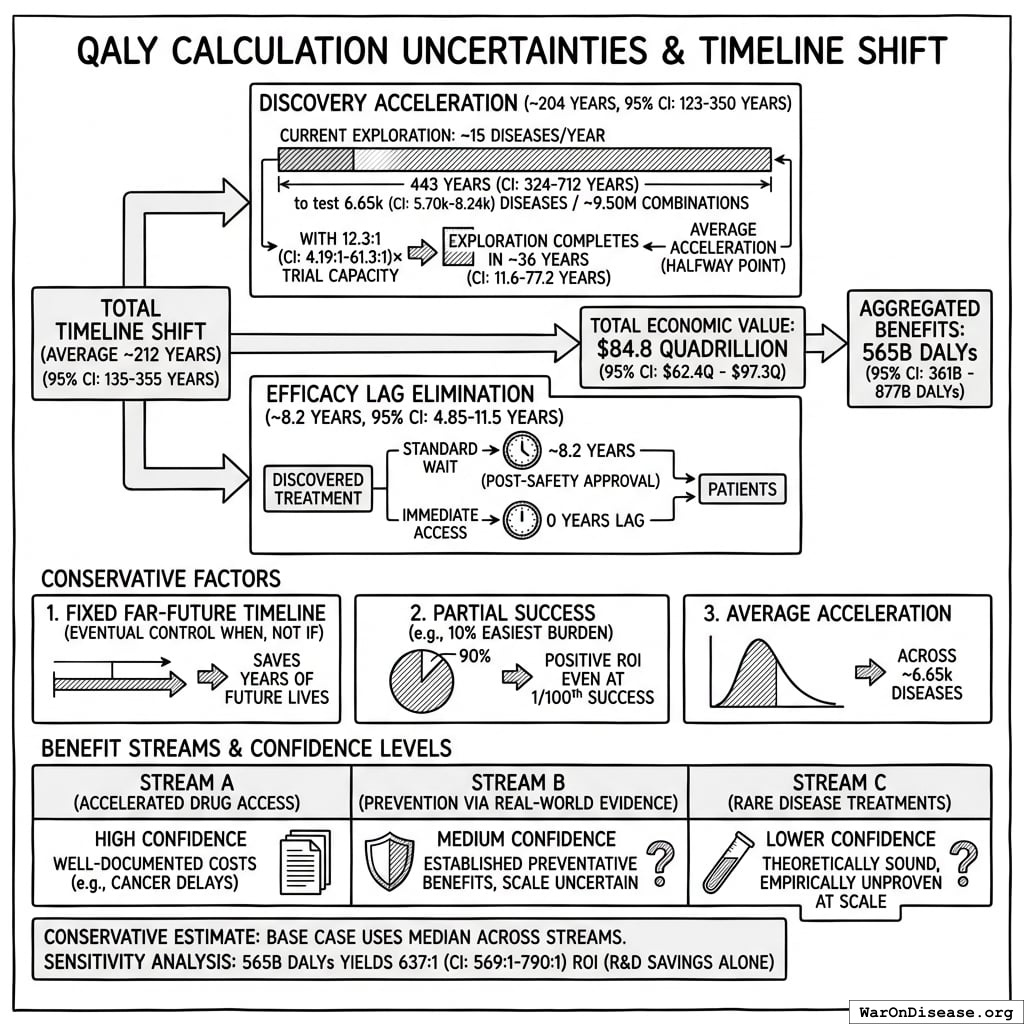
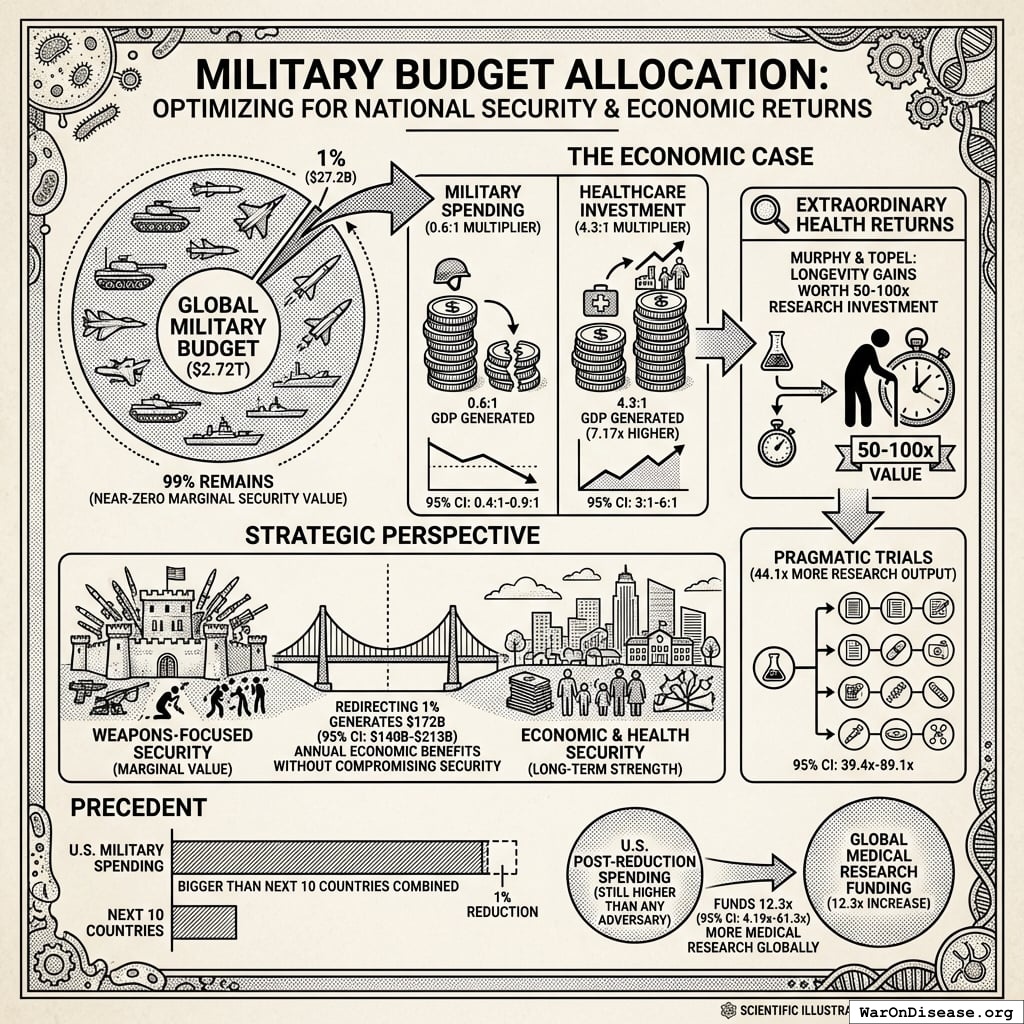
The solution: Redirecting 1% of global military spending ($27.2B/year) to pragmatic clinical trials increases capacity 12.3x (95% CI: 4.19x-61.3x) (to ~185 diseases/year (95% CI: 107 diseases/year-490 diseases/year) treatments/year). Pragmatic trials cost $929 (95% CI: $97-$3K)/patient versus $41K (95% CI: $20K-$120K)/patient for traditional trials, enabling vastly more parallel research. This reduces time to explore all therapeutic possibilities from ~443 years (95% CI: 324 years-712 years) to ~36 years (95% CI: 11.6 years-77.2 years).
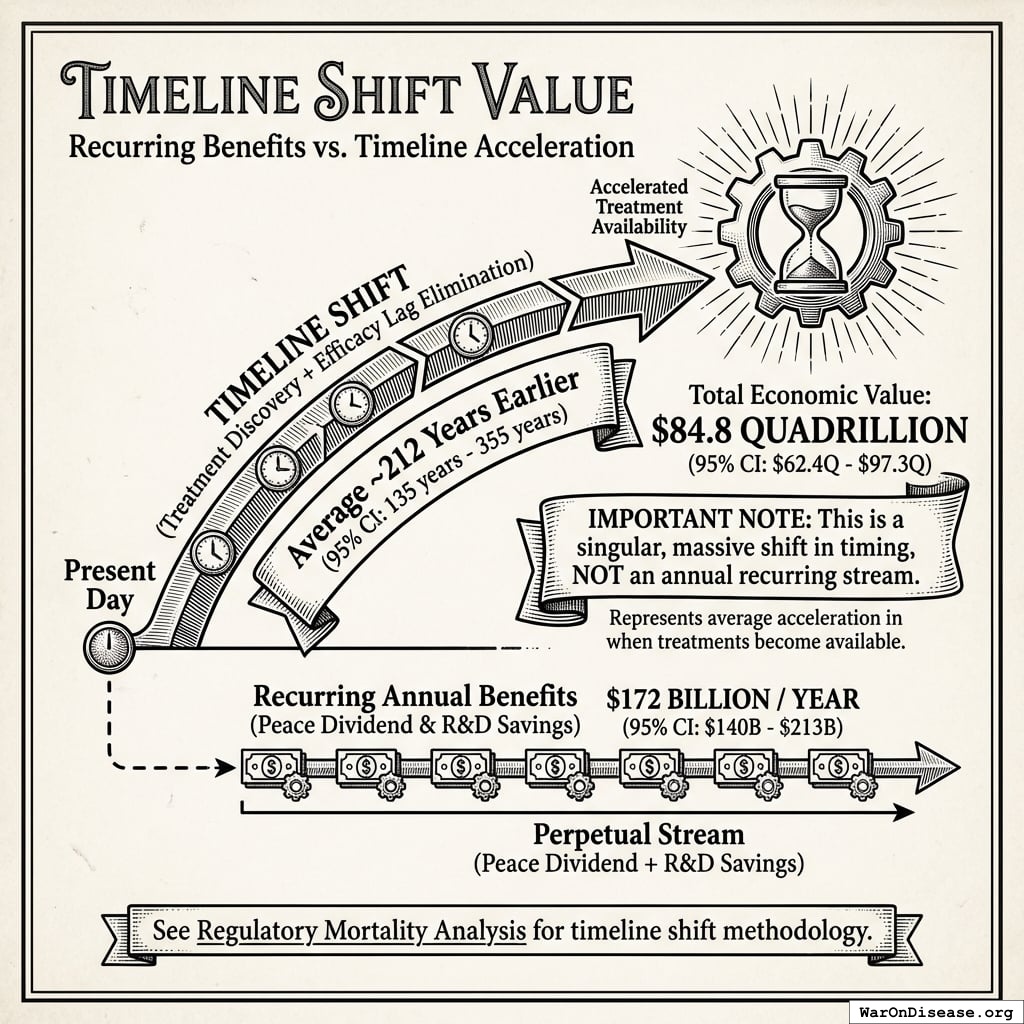
The impact: Treatments that would have taken decades to even begin researching under the status quo get discovered and delivered decades earlier. Combined with eliminating the 8.2 years (95% CI: 4.85 years-11.5 years) regulatory efficacy delay (via opt-in access to ubiquitous trials after Phase I safety), the average treatment reaches patients 212 years (95% CI: 135 years-355 years) sooner. This timeline shift saves 10.7 billion deaths (95% CI: 7.39 billion deaths-16.2 billion deaths), valued at $84.8 quadrillion (95% CI: $62.4 quadrillion-$97.3 quadrillion).
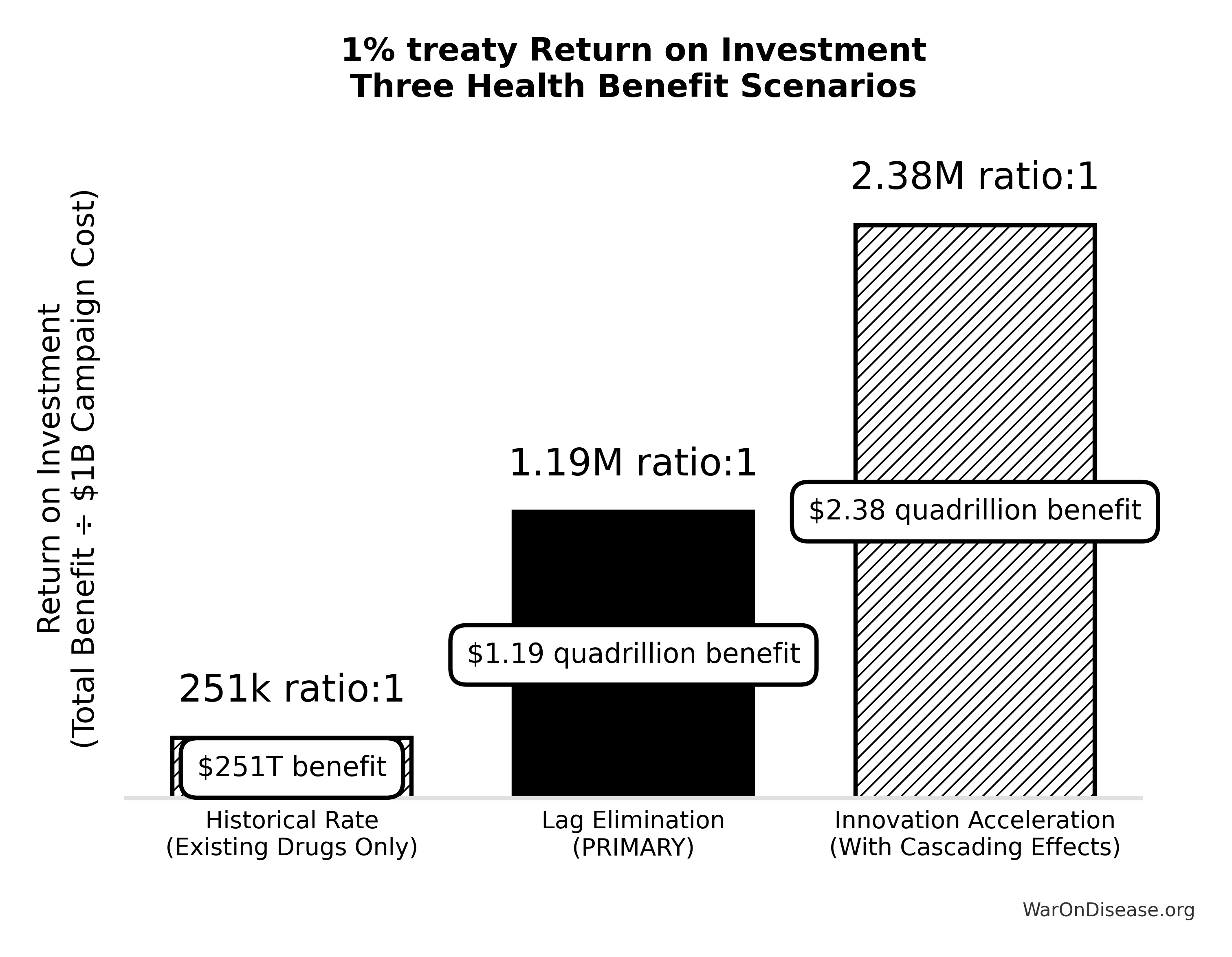
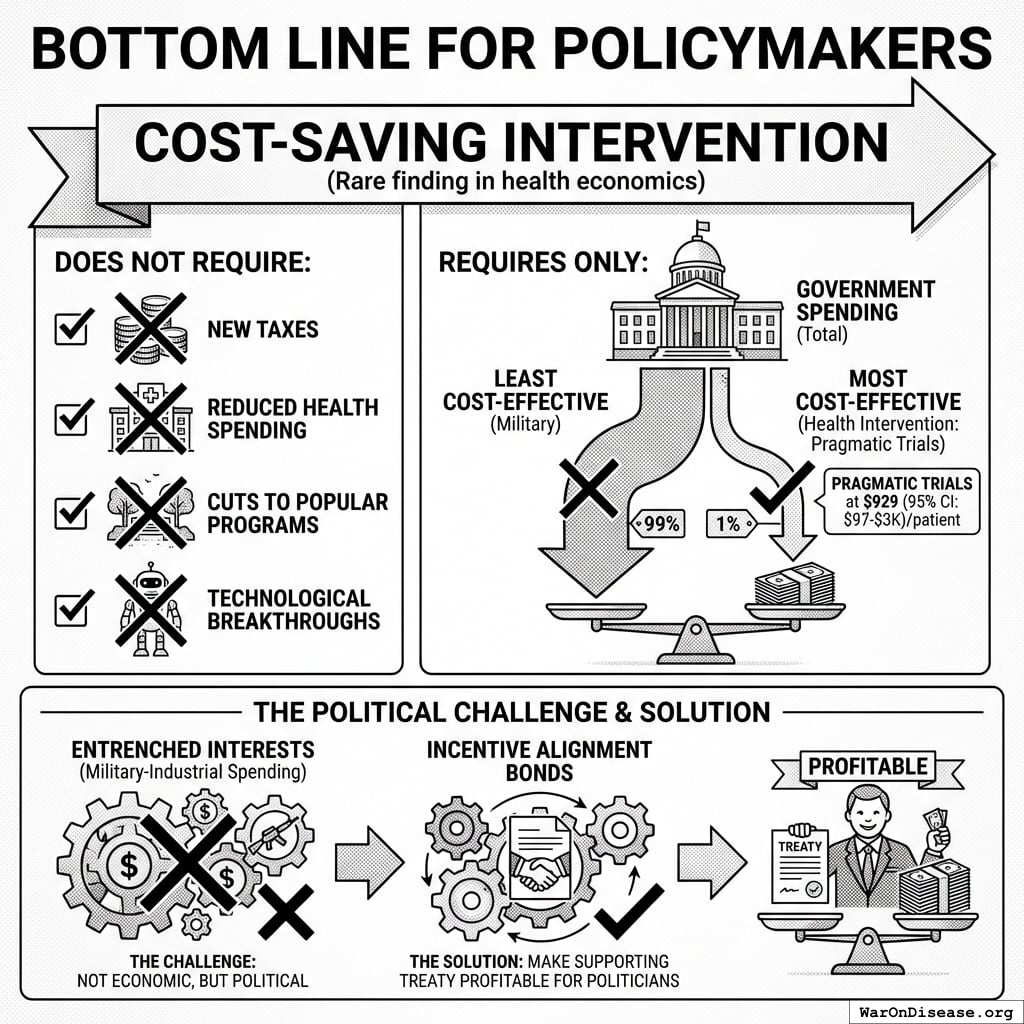
Cost-effectiveness: $0.0018 (95% CI: $0.0007-$0.0041)/DALY via treaty advocacy (50.3kx (95% CI: 23.7kx-111.7kx) better than bed nets) or $0.841 (95% CI: $0.242-$1.75)/DALY via direct funding. ROI ranges from 637:1 (95% CI: 569:1-790:1) (R&D savings only) to 84.8M:1 (95% CI: 46.6M:1-144M:1) (complete benefits). This qualifies as cost-saving: it reduces costs while improving outcomes.
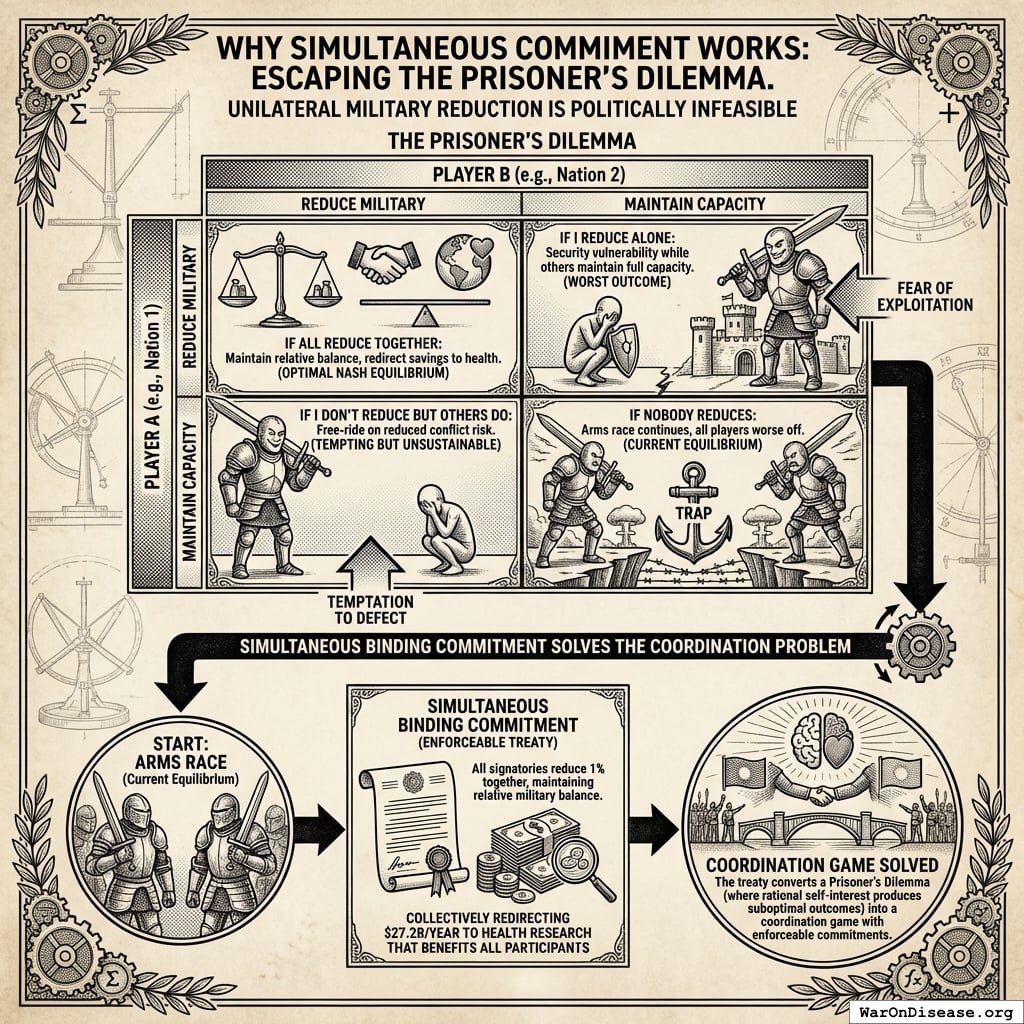
Robustness: Even at 1% (95% CI: 0.1%-10%) probability of treaty adoption, risk-adjusted cost-effectiveness ($0.177 (95% CI: $0.029-$3.20)/DALY) remains 503x (95% CI: 29.9x-3.0kx) better than bed nets. Monte Carlo simulation (10,000 trials) confirms the intervention remains cost-saving across parameter uncertainty. Incentive Alignment Bonds provide the political mechanism: by tying legislators’ electoral support and post-office career prospects to a public voting scorecard, they convert treaty support from political liability to career advantage.
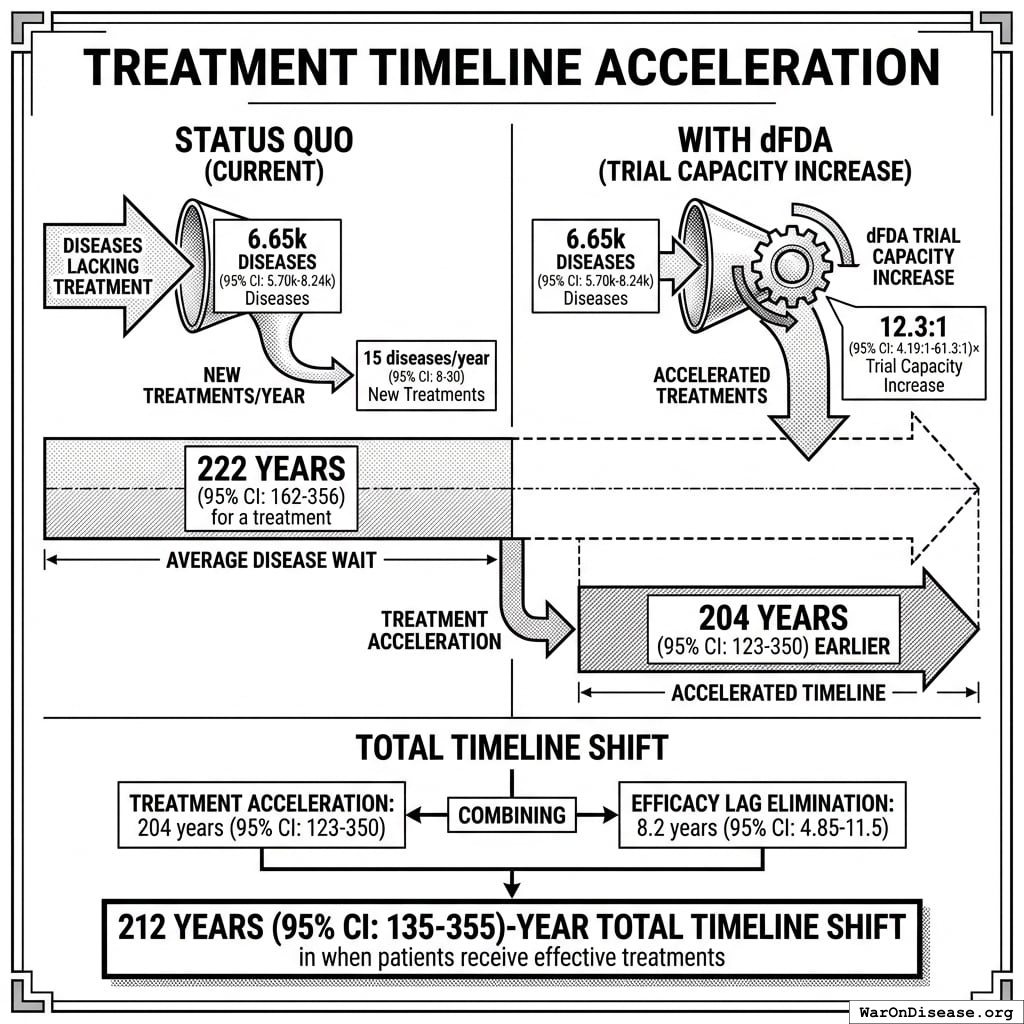
Impact Mechanism: The 212 years (95% CI: 135 years-355 years) average timeline shift combines two complementary effects:
Interpreting the 212 years (95% CI: 135 years-355 years) Timeline Figure: This is a discovery capacity model result, not “time travel” or a prediction that we will achieve results centuries from now. If we must test 9.50 million combinations drug-disease combinations to find all effective treatments, the current system (15 diseases/year (95% CI: 8 diseases/year-30 diseases/year) treatments/year) would take ~443 years (95% CI: 324 years-712 years) to explore this therapeutic search space. Scaling capacity 12.3x (95% CI: 4.19x-61.3x) reduces exploration time to ~36 years (95% CI: 11.6 years-77.2 years). The “212 years (95% CI: 135 years-355 years)” represents the average time a treatment that could be discovered today would have waited under the old system versus the new system. Treatments discovered sooner save lives during the intervening period; this cumulative benefit over the acceleration period yields the headline mortality and economic figures.
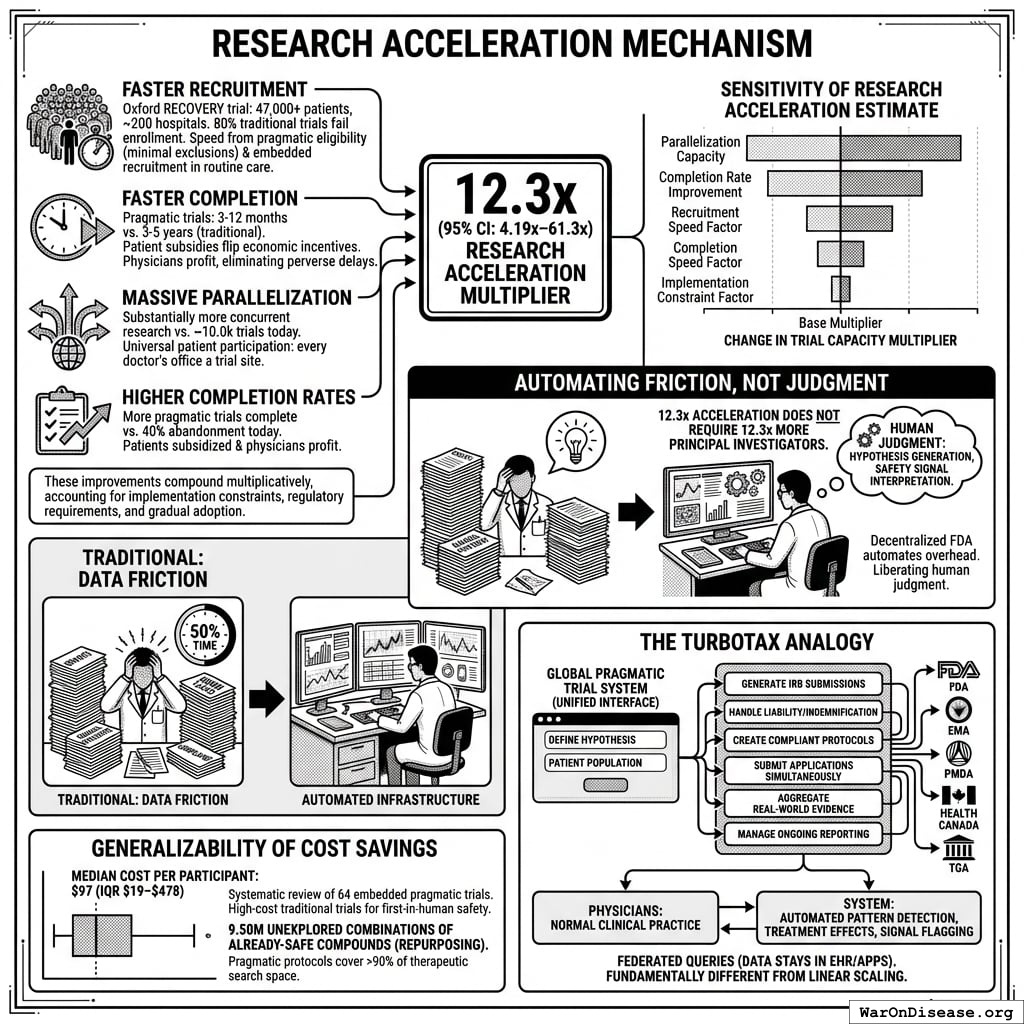
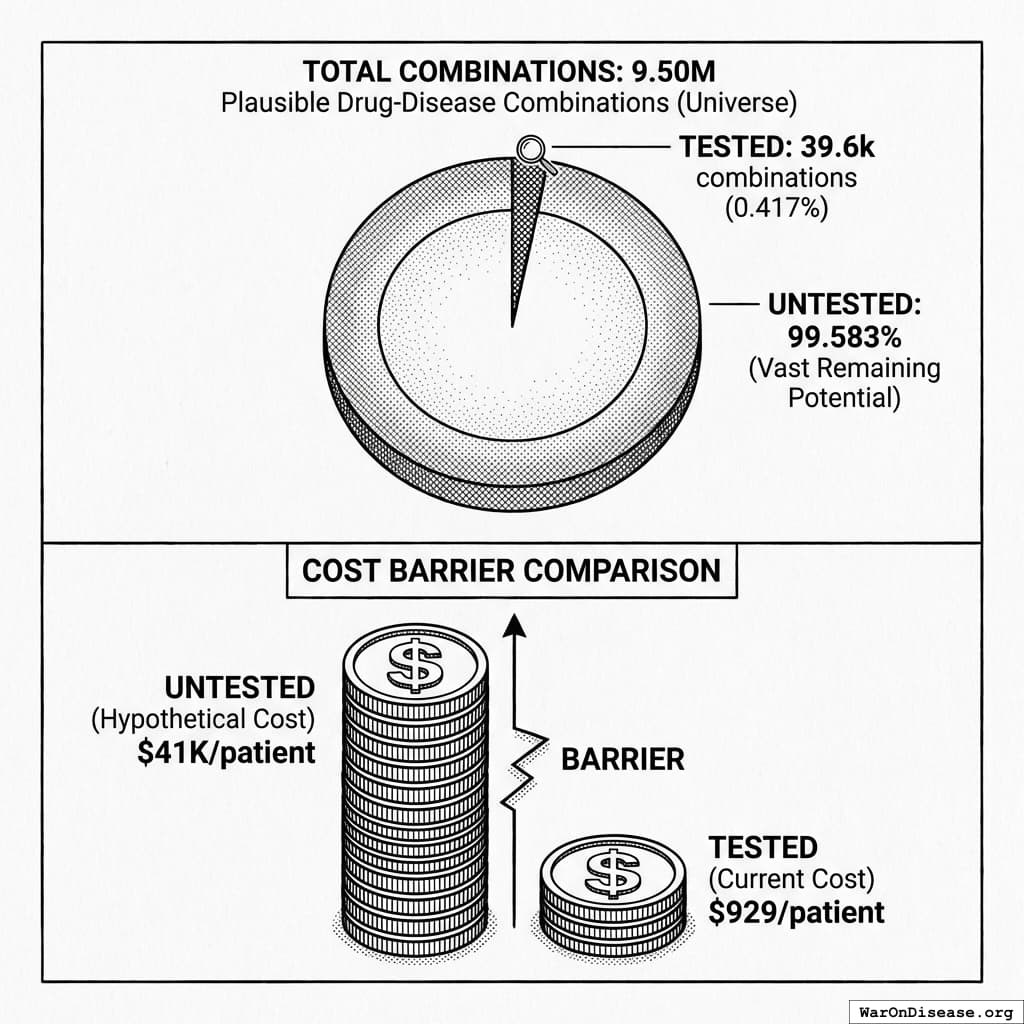
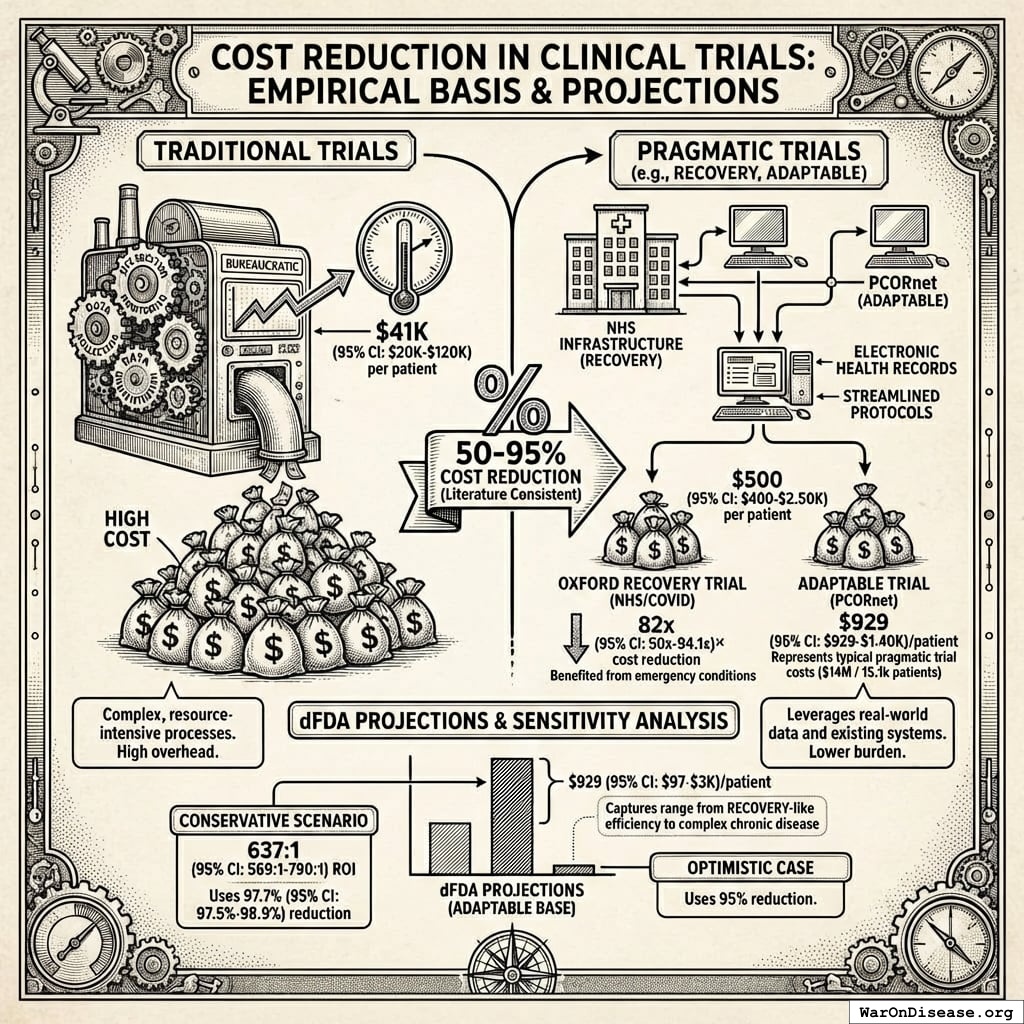
How the 12.3x (95% CI: 4.19x-61.3x) capacity increase works: Redirecting $27.2B/year at $929 (95% CI: $97-$3K)/patient (based on ADAPTABLE trial; RECOVERY achieved $500 (95% CI: $400-$2.50K)/patient under exceptional NHS/COVID conditions) enables 23.4 million patients/year (95% CI: 9.44 million patients/year-96.8 million patients/year) annual trial participants vs. current 1.90 million patients/year (95% CI: 1.50 million patients/year-2.30 million patients/year), increasing trial completion rate from 15 diseases/year (95% CI: 8 diseases/year-30 diseases/year) to 185 diseases/year (95% CI: 107 diseases/year-490 diseases/year). This removes the primary bottleneck to medical progress: currently less than 0.06% of willing patients can access trials, and over 9.50 thousand compounds (95% CI: 7.00 thousand compounds-12.0 thousand compounds) proven-safe compounds (FDA-approved drugs + GRAS substances) remain untested for most conditions they could improve.
Methods: Cost-benefit analysis, NPV calculations, QALY modeling, and ICER analysis using SIPRI military expenditure data, WHO mortality statistics, Harvard meta-analysis of 108 embedded pragmatic trials132, and published clinical trial cost literature. Conservative estimates exclude research acceleration effects; complete estimates include all quantifiable benefits. All parameters, data sources, and uncertainty ranges documented in Parameters and Calculations.
Implications: This intervention corrects a fundamental capital misallocation: military spending creates depreciating assets (weapons become obsolete), while medical research creates appreciating assets (treatments compound in value). Comparable to smallpox eradication (280:1 ROI), it represents the highest-ROI reallocation available to policymakers.
Important limitations: (1) Economic value estimates are cumulative over the ~212 years (95% CI: 135 years-355 years) timeline shift, not annual values. (2) All estimates are conditional on successful treaty implementation. (3) Phase I safety testing remains mandatory. What changes is eliminating post-safety efficacy delays. (4) The “quadrillion dollar” figures represent monetized value of lives saved over centuries of accelerated medical progress, using standard QALY methodology.
Keywords: 1% Treaty, pragmatic clinical trials, regulatory delay, cost-effectiveness analysis, DALY, peace dividend
Primary Findings
The proposal: Redirect 1% of global military spending ($27.2B/year) to fund pragmatic clinical trials that allow patient access after Phase I safety verification, rather than waiting 8.2 years (95% CI: 4.85 years-11.5 years) additional years for Phase II/III efficacy confirmation before patient access.
Bottom line: Cost-saving intervention comparable to smallpox eradication (280:1 ROI).
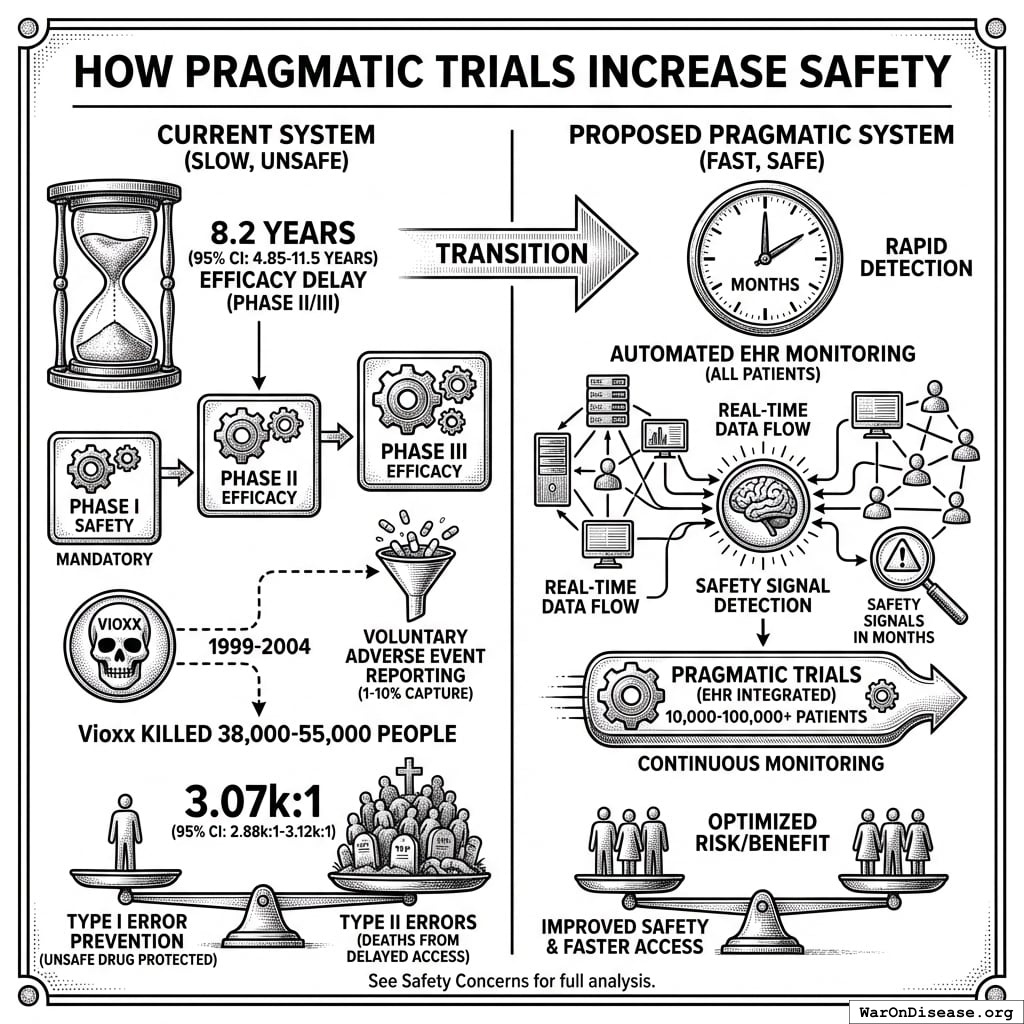
How Pragmatic Trials Increase Safety
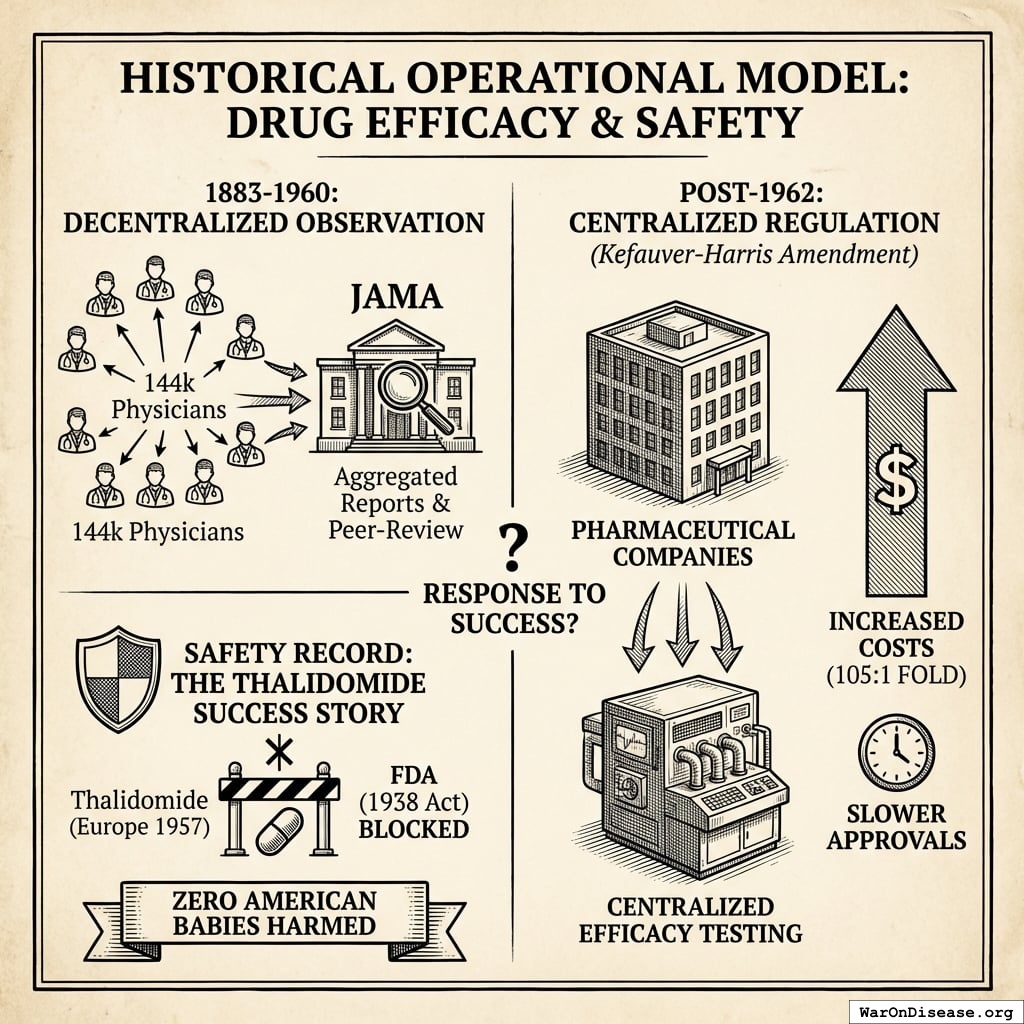
Phase I safety testing remains mandatory. This is the testing that prevented thalidomide in the United States. What changes is eliminating the 8.2 years (95% CI: 4.85 years-11.5 years) efficacy delay (Phase II/III) after safety is verified.
The current system is demonstrably unsafe:
- Vioxx killed 38,000-55,000 people over 5 years (1999-2004) under the “safe” current system because voluntary adverse event reporting captures only 1-10% of events
- Proposed system uses automated EHR monitoring of all patients, detecting safety signals in months instead of years
- Traditional trials test 100-300 patients; pragmatic trials test 10,000-100,000+ patients with continuous monitoring
For every person protected from an unsafe drug (Type I error prevention), the current system kills 3.07k:1 (95% CI: 2.88k:1-3.12k:1) people by delaying access to beneficial treatments (Type II errors). See Safety Concerns for full analysis.
Introduction
Historical Precedents for Grand Challenges
Health economics literature identifies three historical cost-saving interventions:
- Smallpox eradication (1967-1980): 280:1 ROI89, eliminating a disease that killed 300-500 million people in the 20th century alone
- Childhood vaccination programs: Self-funding interventions generating $15B (95% CI: $8.79B-$23.3B) in annual economic benefits7
- Water fluoridation: 23:1 ROI in dental health improvements129
These successes share common features: systemic interventions that address root causes rather than symptoms, positive externalities that compound over time, and political consensus achieved through demonstrated value. They also share a critical limitation: they targeted specific diseases or conditions. No historical intervention has systematically accelerated the discovery process itself.
The Medical Research Bottleneck
Current medical research faces fundamental capacity constraints that limit our ability to discover which treatments actually work:
| Trial participation rate |
0.06% of willing patients |
Massive unmet research capacity11 |
| Untested safe compounds |
9.50 thousand compounds (95% CI: 7.00 thousand compounds-12.0 thousand compounds) proven-safe (FDA-approved drugs + GRAS) |
0.342% (95% CI: 0.21%-0.514%) of drug-disease space explored22 |
| Traditional trial cost |
$41K (95% CI: $20K-$120K)/patient |
Makes comprehensive testing economically infeasible101 |
| Pragmatic trial cost |
$929 (95% CI: $97-$3K)/patient |
44.1x (95% CI: 39.4x-89.1x) cost reduction enables systematic exploration (review of 108 embedded pragmatic trials, 64 with cost data132) |
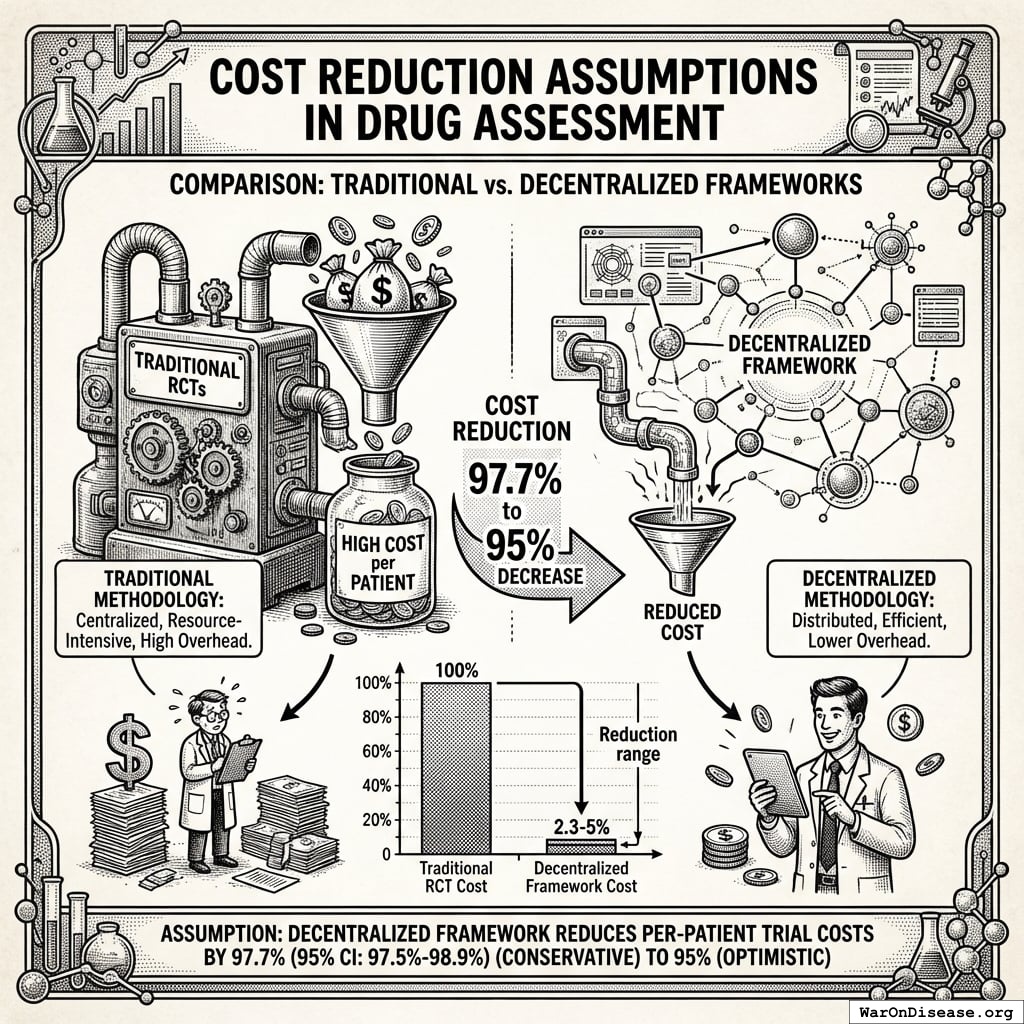
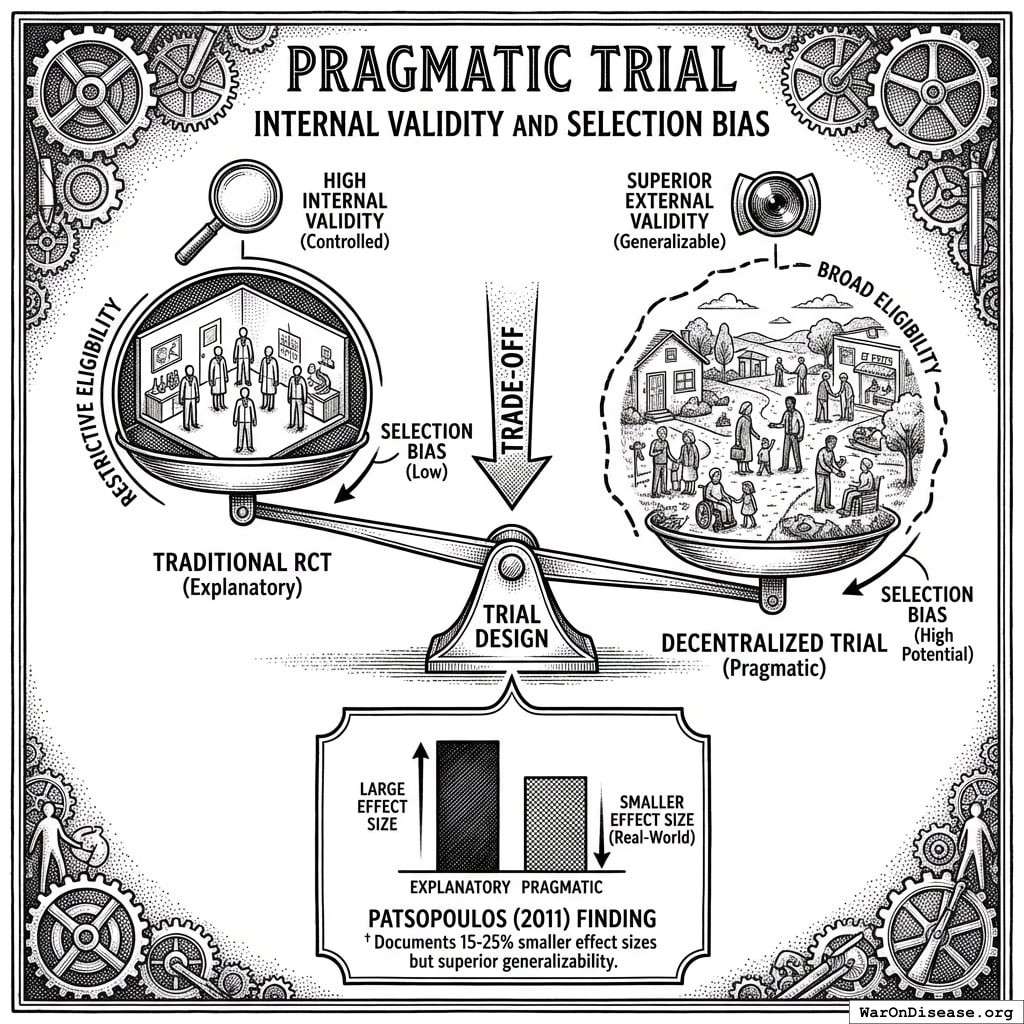
Multiple large-scale pragmatic trials and systematic reviews demonstrate that pragmatic trial design maintains scientific rigor while dramatically reducing costs. A Harvard review of 108 embedded pragmatic trials (64 with cost data) found median costs of $97/patient132. The Oxford RECOVERY trial achieved $500 (95% CI: $400-$2.50K)/patient (under exceptional NHS/COVID conditions), while the PCORnet ADAPTABLE trial achieved $929 (95% CI: $929-$1.40K)/patient under normal conditions1. Our system projections use the conservative ADAPTABLE estimate ($929 (95% CI: $97-$3K)/patient). This 44.1x (95% CI: 39.4x-89.1x) cost reduction transforms the economics of medical research: what was previously too expensive to test becomes systematically explorable.
Contribution to Literature
Key Contributions to Health Economics Literature:
- Regulatory delay cost quantification
- Trial capacity expansion benefits
- Cost-effectiveness under political uncertainty
- Self-sustaining funding mechanism
- Incentive Alignment Bonds align investors, politicians, patients
- Converts military spending (0.6x (95% CI: 0.4x-0.9x) economic multiplier) → health research (4.3x (95% CI: 3x-6x) multiplier)
- Legally-binding treaty with market-based incentives
- No reliance on altruism or bureaucratic mandate
The analysis that follows uses standard cost-benefit methodology (NPV, QALY modeling, ICER analysis) applied to SIPRI military expenditure data, WHO mortality statistics, and published clinical trial cost literature. All parameter uncertainty is quantified through Monte Carlo simulation (10,000 trials) with tornado diagrams identifying key drivers of variance.
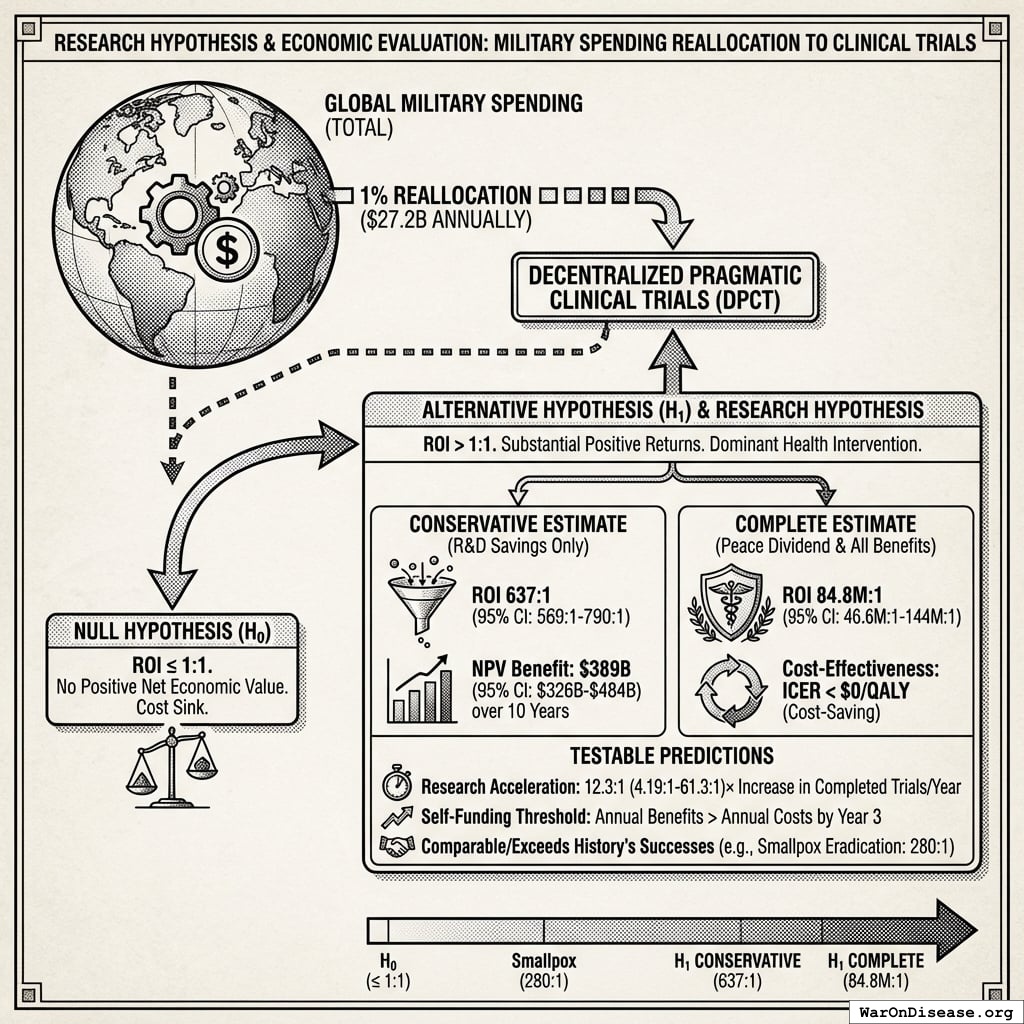
Research Hypothesis
Primary Hypothesis: Reallocating 1% of global military spending ($27.2B annually) to fund decentralized pragmatic clinical trials generates return on investment between 637:1 (95% CI: 569:1-790:1) (conservative estimate, R&D savings only) and 84.8M:1 (95% CI: 46.6M:1-144M:1) (complete estimate, including peace dividend and all direct benefits), representing a dominant health intervention that simultaneously reduces costs while improving health outcomes.
Null Hypothesis (H₀): The intervention does not generate positive net economic value (ROI ≤ 1:1)
Alternative Hypothesis (H₁): The intervention generates substantial positive returns (ROI > 1:1), comparable to or exceeding history’s most successful public health interventions (smallpox eradication: 280:189)
Testable Predictions:
- Conservative case: NPV benefit of $389B (95% CI: $326B-$484B) over 10 years horizon
- Cost-effectiveness: Cost per DALY < $0 (cost-saving while improving health)
- Research acceleration: 12.3x (95% CI: 4.19x-61.3x) increase in completed trials per year
- Self-funding threshold: Annual benefits exceed annual costs by year 3 of implementation
Nomenclature and Key Terms
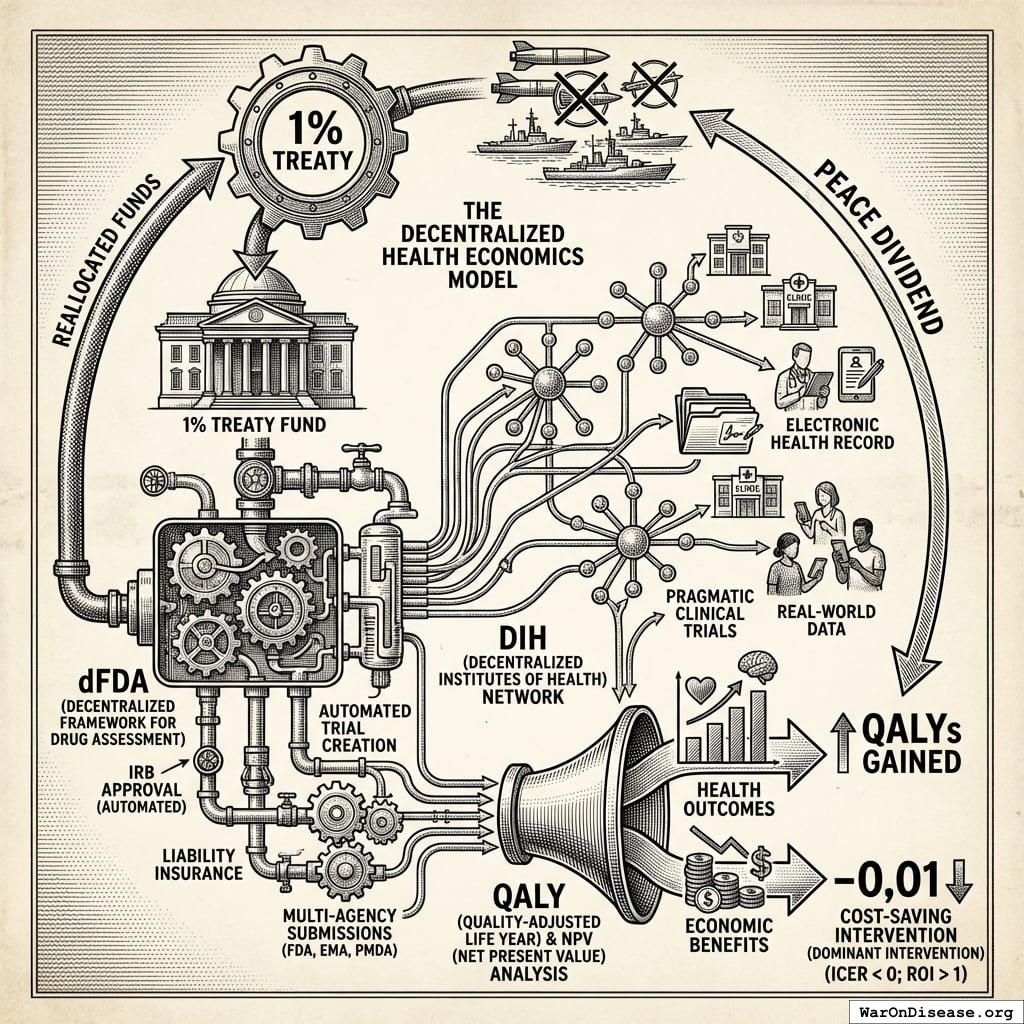
A Decentralized FDA: A regulatory wrapper that automates trial creation, IRB approval, liability insurance, and simultaneous multi-agency submissions (FDA, EMA, PMDA, etc.) across countries. Like TurboTax abstracts away tax code complexity, the system abstracts away regulatory complexity: researchers define hypotheses, and the system handles compliance. Uses real-world data, electronic health records, and decentralized patient participation. Reduces per-patient costs by 50-95% compared to traditional trials.
A decentralized institutes of health: A pattern for decentralized, programmable, and democratic organizations that implement health initiatives. A decentralized institutes of health can be funded by a 1% Treaty Fund to subsidize patient participation in pragmatic clinical trials.
Peace Dividend: Economic benefits from reduced military spending, including fiscal savings, reduced conflict-related economic damage, and favorable economic multiplier effects from reallocating resources to productive sectors.
Cost-Saving Intervention (technical term: “dominant intervention”): Interventions that both reduce costs AND improve health outcomes. Generally recommended regardless of willingness-to-pay thresholds (e.g., vaccination programs, smoking cessation).
A 1% Treaty: Proposed international agreement where signatory nations commit to reducing military expenditure by 1% and redirecting those funds ($27.2B globally) to pragmatic clinical trials infrastructure.
\[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\]
A 1% Treaty Fund: The treasury that receives and allocates the 1% of military spending reallocated by the 1% Treaty. It funds pragmatic clinical trials, which can be implemented through networks of decentralized institutes of health.
Pragmatic Clinical Trial: Trial design using real-world settings and broad eligibility criteria rather than highly controlled laboratory conditions, improving generalizability and dramatically reducing costs. Examples: Oxford RECOVERY (COVID, 47,000 patients), PCORnet ADAPTABLE (cardiovascular, 15.1 thousand patients), and 108+ trials documented in Harvard meta-analysis132.
Problem Statement
Current Resource Allocation
Humanity’s budget priorities, explained simply:
\[
\begin{gathered}
Ratio_{mil:RD} \\
= \frac{Spending_{mil}}{Spending_{RD}} \\
= \frac{\$2.72T}{\$67.5B} \\
= 40.3
\end{gathered}
\]
Understanding the comparison: While total government medical research spending is $67.5B (95% CI: $54B-$81B) (including basic research, translational research, and clinical trials), government clinical trial funding is only $4.50B (95% CI: $3B-$6B). The 1% treaty redirects $27.2B to pragmatic clinical trials, increasing government clinical trial funding ~7-fold.
The bottleneck isn’t basic research or laboratory science. It’s clinical trials. We’ve tested 0.342% (95% CI: 0.21%-0.514%) of possible drug-disease combinations using existing safe compounds. Not because the science is impossible, but because traditional trials cost $41K (95% CI: $20K-$120K) while pragmatic trials like Oxford RECOVERY run for $500 (95% CI: $400-$2.50K). At current funding levels, testing the remaining 99.7% (95% CI: 99.5%-99.8%) of therapeutic space would take millennia. Meanwhile, military budgets dwarf the funding needed to automate ubiquitous clinical trials and systematically explore what actually helps people.
Disease treatment vs. curing disease
\[
\begin{gathered}
Burden_{disease} \\
= Cost_{medical,direct} + Loss_{life,disease} \\
+ Loss_{productivity} \\
= \$9.9T + \$94.2T + \$5T \\
= \$109T
\end{gathered}
\]
That’s 0.0525% (95% CI: 0.0474%-0.0588%) of the disease burden spent on actually fixing the problem:
\[
\begin{gathered}
Pct_{RD:burden} \\
= \frac{Spending_{RD}}{Cost_{health+war}} \\
= \frac{\$67.5B}{\$129T} \\
= 0.0525\%
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{health+war} \\
= Cost_{war,total} + Burden_{disease} + Spending_{symptom} \\
= \$11.4T + \$109T + \$8.2T \\
= \$129T
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{war,total} \\
= Cost_{war,direct} + Cost_{war,indirect} \\
= \$7.66T + \$3.7T \\
= \$11.4T
\end{gathered}
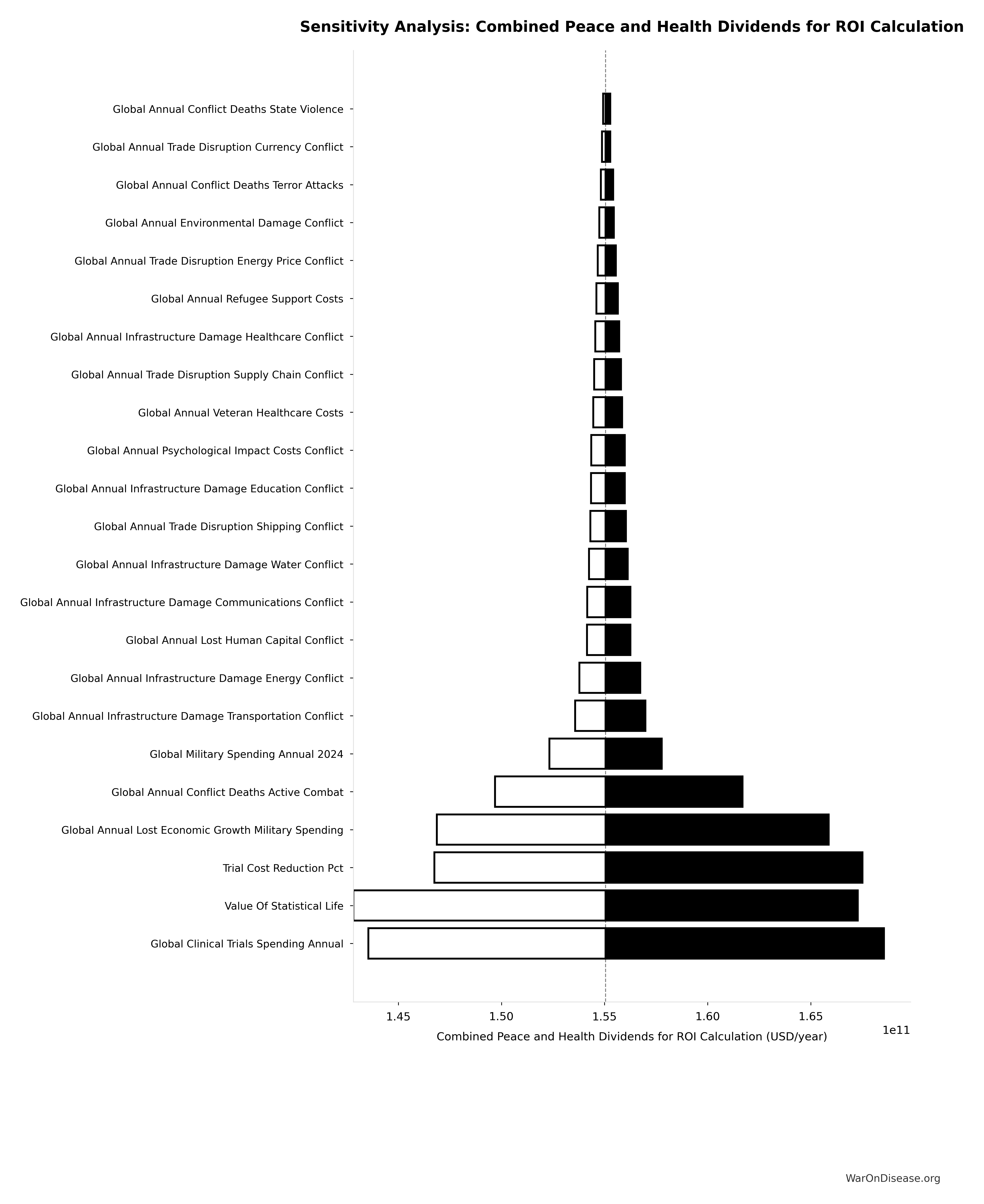
\] where: \[
\begin{gathered}
Cost_{war,direct} \\
= Loss_{life,conflict} + Damage_{infra,total} \\
+ Disruption_{trade} + Spending_{mil} \\
= \$2.45T + \$1.88T + \$616B + \$2.72T \\
= \$7.66T
\end{gathered}
\] where: \[
\begin{gathered}
Loss_{life,conflict} \\
= Cost_{combat,human} + Cost_{state,human} \\
+ Cost_{terror,human} \\
= \$2.34T + \$27B + \$83B \\
= \$2.45T
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{combat,human} \\
= Deaths_{combat} \times VSL \\
= 234{,}000 \times \$10M \\
= \$2.34T
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{state,human} \\
= Deaths_{state} \times VSL \\
= 2{,}700 \times \$10M \\
= \$27B
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{terror,human} \\
= Deaths_{terror} \times VSL \\
= 8{,}300 \times \$10M \\
= \$83B
\end{gathered}
\] where: \[
\begin{gathered}
Damage_{infra,total} \\
= Damage_{comms} + Damage_{edu} + Damage_{energy} \\
+ Damage_{health} + Damage_{transport} + Damage_{water} \\
= \$298B + \$234B + \$422B + \$166B + \$487B + \$268B \\
= \$1.88T
\end{gathered}
\] where: \[
\begin{gathered}
Disruption_{trade} \\
= Disruption_{currency} + Disruption_{energy} \\
+ Disruption_{shipping} + Disruption_{supply} \\
= \$57.4B + \$125B + \$247B + \$187B \\
= \$616B
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{war,indirect} \\
= Damage_{env} + Loss_{growth,mil} + Loss_{capital,conflict} \\
+ Cost_{psych} + Cost_{refugee} + Cost_{vet} \\
= \$100B + \$2.72T + \$300B + \$232B + \$150B + \$200B \\
= \$3.7T
\end{gathered}
\] where: \[
\begin{gathered}
Burden_{disease} \\
= Cost_{medical,direct} + Loss_{life,disease} \\
+ Loss_{productivity} \\
= \$9.9T + \$94.2T + \$5T \\
= \$109T
\end{gathered}
\]
Mortality and Morbidity Burden
The World Health Organization reports 150 thousand deaths/day4 daily deaths from disease and aging. Many of these are eventually avoidable with accelerated biomedical progress (55.0 million deaths/year (95% CI: 46.6 million deaths/year-63.2 million deaths/year) annually).
This mortality burden exceeds:
\[
\begin{gathered}
Ratio_{dis:terror} \\
= \frac{Deaths_{curable,ann}}{Deaths_{9/11}} \\
= \frac{55M}{3{,}000} \\
= 18{,}400
\end{gathered}
\]
\[
\begin{gathered}
Ratio_{dis:war} \\
= \frac{Deaths_{curable,ann}}{Deaths_{conflict}} \\
= \frac{55M}{245{,}000} \\
= 225
\end{gathered}
\] where: \[
\begin{gathered}
Deaths_{conflict} \\
= Deaths_{combat} + Deaths_{state} + Deaths_{terror} \\
= 234{,}000 + 2{,}700 + 8{,}300 \\
= 245{,}000
\end{gathered}
\]
Despite this disparity in mortality burden, resource allocation heavily favors security spending over medical research and curative interventions.
How It Works
The mechanism is financial, not bureaucratic:
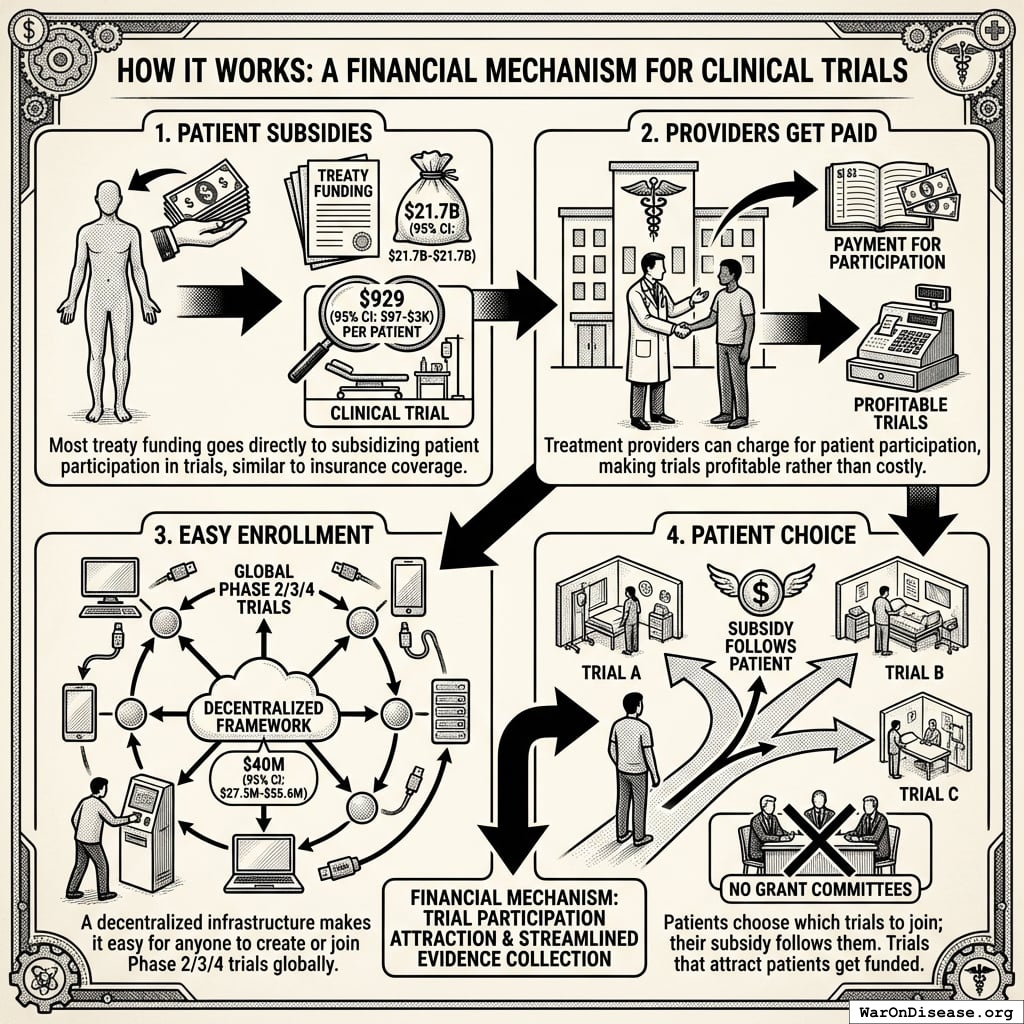
- Patient subsidies: Most treaty funding ($21.7B (95% CI: $21.7B-$21.7B)) goes directly to subsidizing patient participation in trials at ~$929 (95% CI: $97-$3K)1 per patient, similar to how insurance covers medical procedures
- Providers get paid: Treatment providers can charge for patient participation in trials, making trials profitable rather than costly
- Easy enrollment: A decentralized FDA infrastructure (costing just $40M (95% CI: $27.3M-$55.6M)) makes it easy for anyone to create or join Phase 2/3/4 trials globally
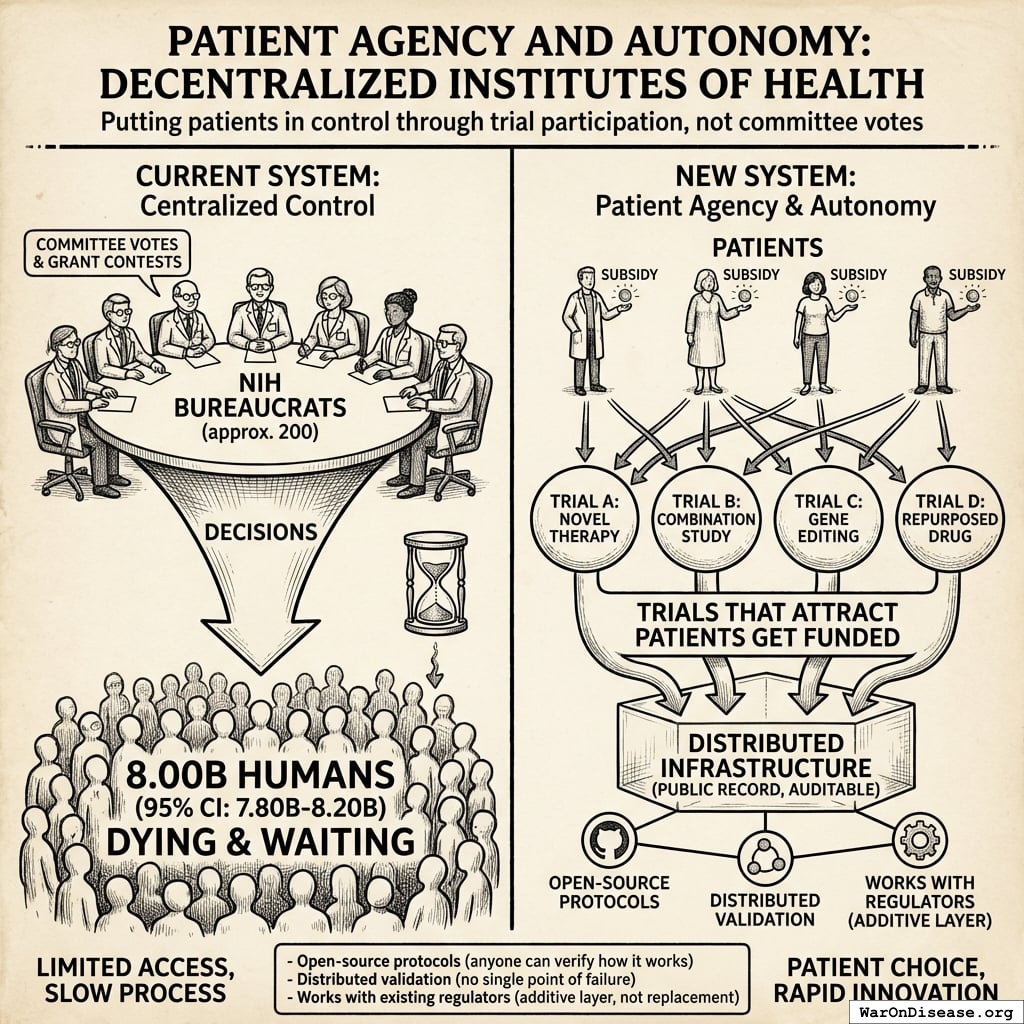
- Patient choice: Patients choose which trials to join; their subsidy follows them. Trials that attract patients get funded. No grant committees deciding what’s “worthy.”
The mechanism makes trial participation financially attractive for both patients and providers while streamlining evidence collection through existing healthcare delivery infrastructure.
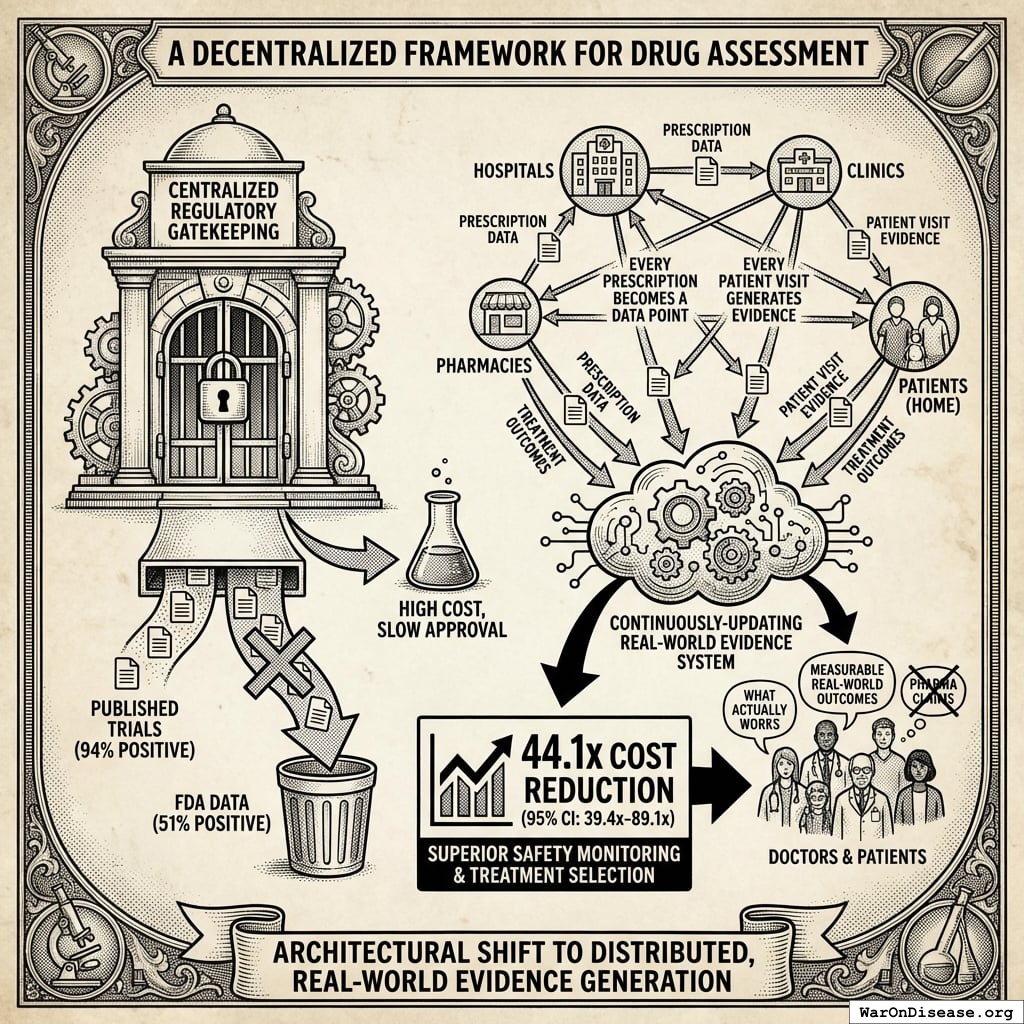
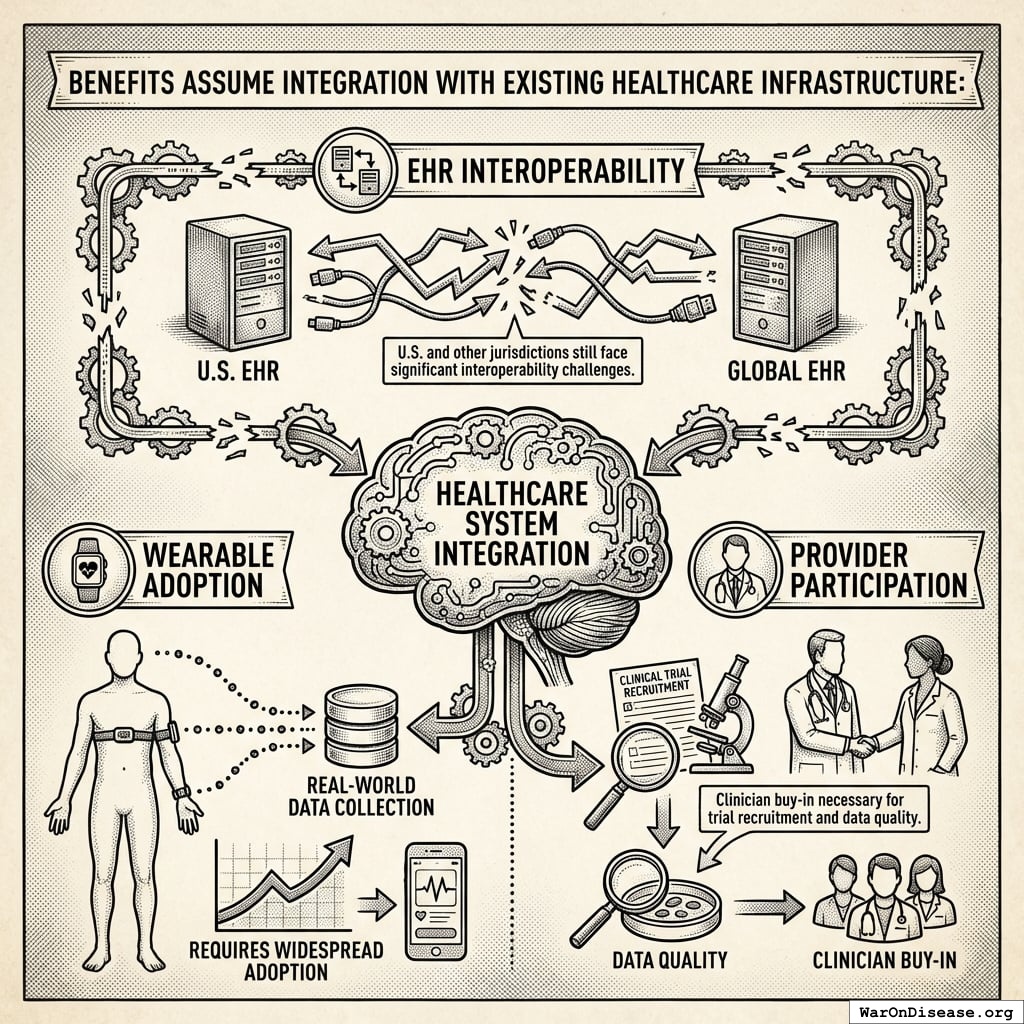
A Decentralized Framework for Drug Assessment
The economic model assumes integration of pragmatic trial infrastructure into standard healthcare delivery. Every prescription becomes a data point. Every patient visit generates evidence. Every treatment outcome feeds into a continuously-updating system that tells doctors and patients what actually works. Not what pharmaceutical companies claim works (published trials show 94% positive results while FDA data shows only 51%133), but what measurably happens to real humans taking real treatments.
This architectural shift from centralized regulatory gatekeeping to distributed, real-world evidence generation achieves a 44.1x (95% CI: 39.4x-89.1x) cost reduction while providing superior safety monitoring and treatment selection capabilities.
\[
\begin{gathered}
k_{reduce} \\
= \frac{Cost_{P3,pt}}{Cost_{pragmatic,pt}} \\
= \frac{\$41K}{\$929} \\
= 44.1
\end{gathered}
\]
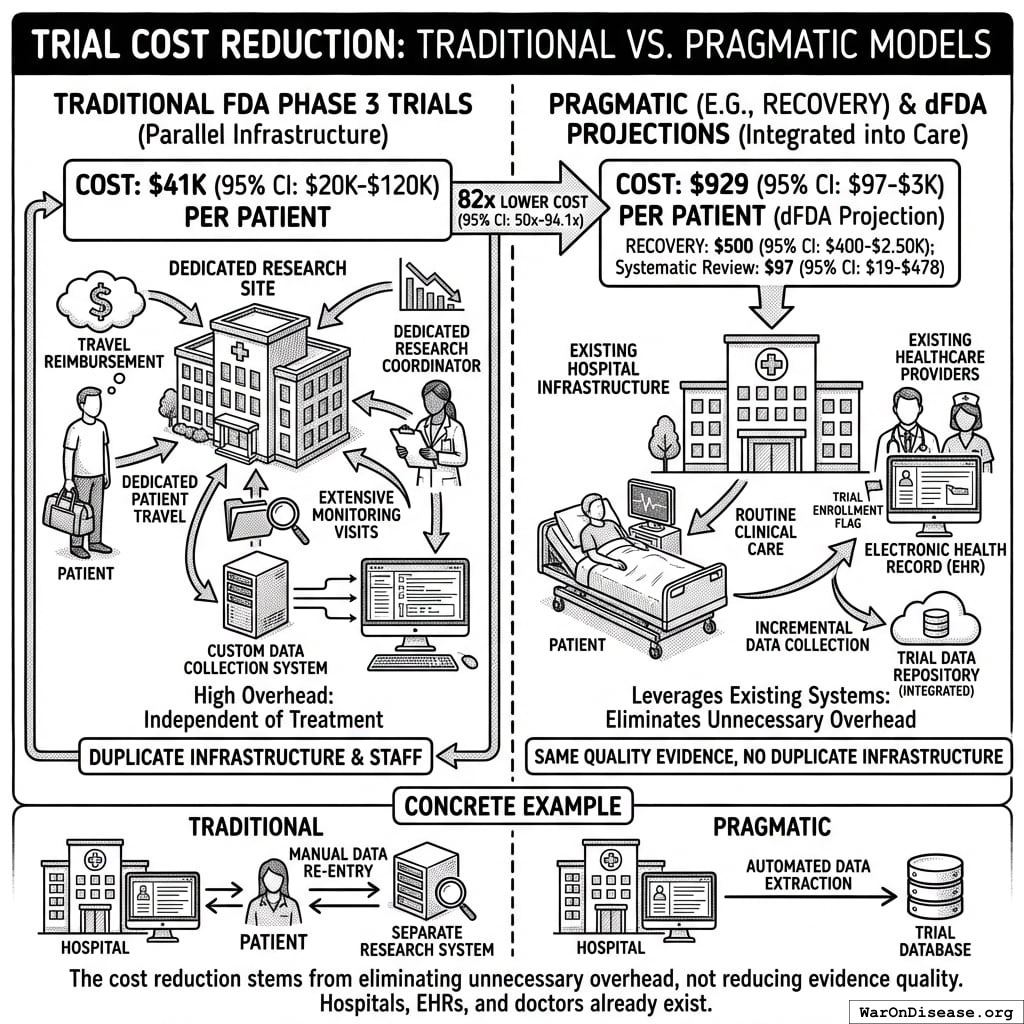
Trial Cost Reduction
Traditional FDA Phase 3 trials cost $41K (95% CI: $20K-$120K)101 per patient because they require dedicated infrastructure: specialized research sites, dedicated research coordinators, custom data collection systems, patient travel reimbursement, and extensive monitoring visits. This overhead exists independent of the actual treatment being tested.
The Oxford RECOVERY trial demonstrated an alternative: leverage existing hospital infrastructure, collect only incremental data beyond standard medical records, and integrate evidence generation into routine clinical care. Cost: $500 (95% CI: $400-$2.50K)83 per patient. (Note: RECOVERY benefited from NHS/COVID conditions; however, a systematic review of 64 pragmatic trials found a median cost of $97 (95% CI: $19-$478)/patient74, confirming this efficiency is replicable. Our system projections use a conservative $929 (95% CI: $97-$3K)/patient based on the ADAPTABLE trial.) Same quality evidence. 82x (95% CI: 50x-94.1x) lower cost.
Concrete example: A hospital already tracks patient lab results, symptoms, and outcomes in electronic health records. Traditional trials build a parallel research infrastructure to collect the same information again. Pragmatic trials simply flag which patients are enrolled and automatically extract relevant data from existing systems. No duplicate infrastructure, no dedicated research staff per trial.
The cost reduction stems from eliminating unnecessary overhead, not reducing evidence quality. Hospitals already exist. Electronic health records already exist. Doctors already see patients. The trial infrastructure simply uses what’s already there rather than building dedicated research facilities.
\[
\begin{gathered}
k_{RECOVERY} \\
= \frac{Cost_{P3,pt}}{Cost_{RECOVERY,pt}} \\
= \frac{\$41K}{\$500} \\
= 82
\end{gathered}
\]
Enhanced Safety Monitoring
Current system limitations: If a drug causes liver damage in 1% of patients, this pattern often goes undetected until 100,000+ prescriptions have been written, because adverse event reporting is voluntary. Doctors must notice the problem, remember to file a report, and complete the paperwork. Average reporting rate approximately 6%134, meaning ~94% of adverse events go unreported.
Concrete failure case: Rofecoxib (Vioxx)135, approved in 1999 for arthritis pain, increased cardiovascular event risk (heart attacks and strokes) through COX-2 enzyme inhibition. The cardiovascular signal went undetected for 5 years despite 92.8 million U.S. prescriptions (1999-2003)135. Voluntary adverse event reporting failed to identify the pattern until dedicated post-market studies confirmed the association in 2004, leading to withdrawal. Estimates of deaths from the delay range from 38,000 (Lancet) to 55,000 (FDA testimony)135. Continuous EHR monitoring of cardiovascular events (heart attacks, strokes, ER visits) across millions of patients would have detected the elevated rate within months, not years, as these outcomes are objectively captured in hospital records.
Integrated surveillance alternative: Every prescription automatically becomes a tracked data point. When patients experience cardiovascular events, get lab tests, or visit emergency rooms, the system captures these outcomes via existing EHR infrastructure. No extra paperwork required. Like credit card fraud detection systems that identify suspicious patterns across millions of transactions in real-time, integrated health systems can detect treatment-associated adverse events across millions of patients automatically.
The system automatically aggregates outcomes:
- 10,000 patients prescribed Drug X → System tracks all subsequent cardiovascular events, ER visits, lab results, and hospitalizations via existing EHR infrastructure
- 120 patients (1.2%) show elevated cardiovascular event rates within 90 days → Automated statistical flag triggers when pattern exceeds expected background rate for matched controls
- Pattern detected after 5,000 prescriptions → Public alert issued to all prescribing physicians and patients, rather than waiting for years and dedicated post-market studies
- Mass notification system → All patients currently taking the drug receive automated alerts through patient portals, enabling immediate clinical review and alternative treatment consideration
Detection timeline comparison (Vioxx cardiovascular risk135):
- Actual detection with voluntary reporting: 5 years from approval (1999) to withdrawal (2004), 38,000-55,000 estimated deaths135
- Projected with ubiquitous EHR monitoring: 6-12 months from widespread use to pattern detection (automated cardiovascular event surveillance comparing treated patients to matched controls)
This infrastructure is not hypothetical. The136 currently monitors 128.7 million patients across US health systems for drug safety signals using similar distributed data methodology. The proposed system makes this the default infrastructure for all treatments from day one, rather than a separate monitoring program activated only after problems are suspected. This represents a fundamental safety improvement: continuous, automated, population-scale adverse event detection with immediate mass notification capability, rather than relying on voluntary physician reporting (which captures only ~6% of actual adverse events)134 and slow manual review processes.
Comparative Effectiveness Rankings
Current decision-making: Doctor prescribes treatments based on pharmaceutical marketing, medical school training from years ago, and whatever clinical experiences they happen to remember. Patient has no access to comparative effectiveness data.
Evidence-based alternative: Doctor searches “rheumatoid arthritis treatment” in the integrated evidence system, sees treatments ranked by measured effectiveness in real-world patients:
Rankings show frequency and magnitude of outcome changes across actual patient populations. Filters allow stratification: “Show me effectiveness in women over 50 with my patient’s genetic markers and comorbidities.” This precision medicine approach shows what works for patients like yours, not what works on average across everyone.
Like Amazon rankings based on verified purchase reviews, except based on measured clinical outcomes rather than subjective opinions, and stratified by patient characteristics rather than averaged across all users.
Implementation: The system already has prescription records and outcome data from routine care. Ranking is just aggregation and sorting. No new data collection needed, just making existing data actually useful for treatment decisions.
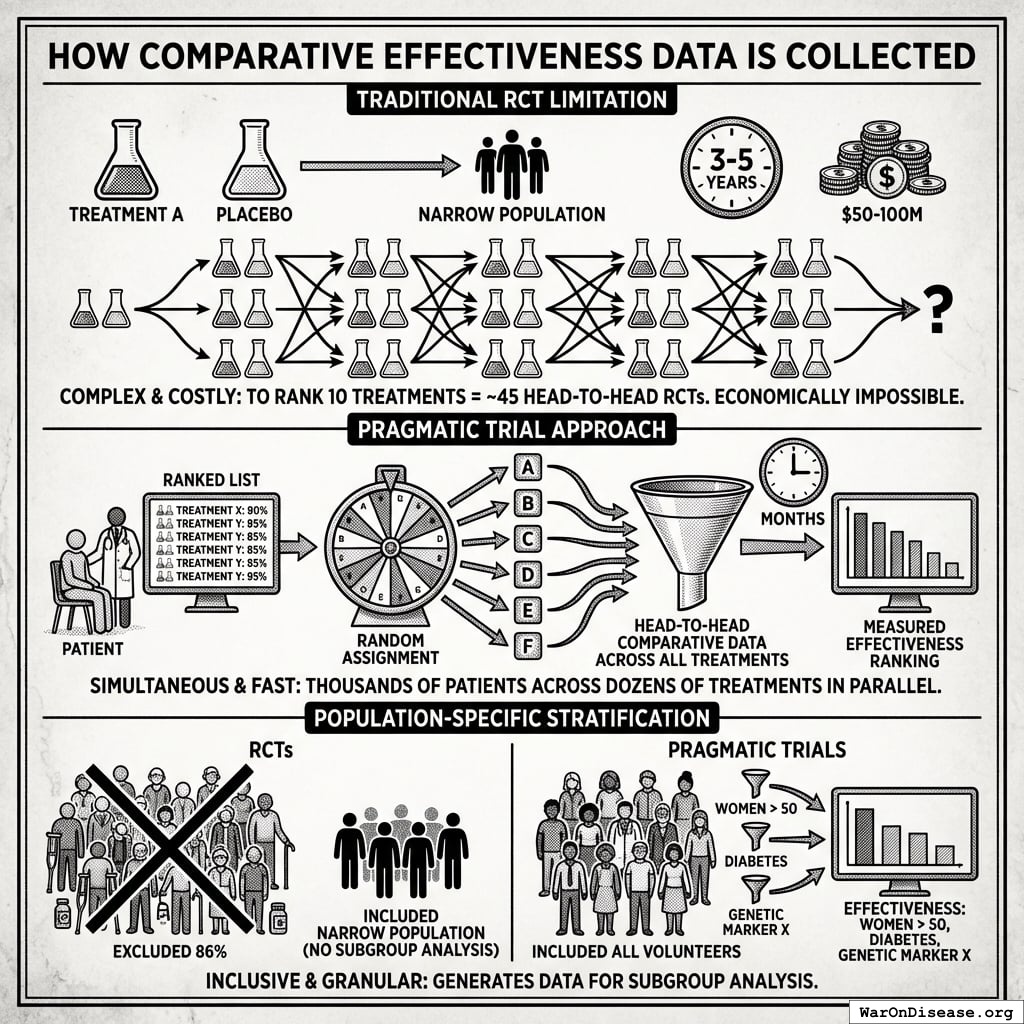
How Comparative Effectiveness Data Is Collected
Traditional RCT limitation: Standard trials compare one treatment vs. placebo (or occasionally one active comparator). To rank 10 treatments for a condition, you would need ~45 separate head-to-head RCTs, each costing $50-100M and taking 3-5 years. This is economically impossible for most conditions.
Pragmatic trial approach: When a patient volunteers for treatment of their condition, physicians access a ranked list of all safe treatments with demonstrated or theoretical efficacy based on existing evidence. The patient is then randomly assigned to one of these treatment options. This randomization serves dual purposes:
- For the patient: Equal chance of receiving any potentially effective treatment
- For medical knowledge: Generates comparative effectiveness data across all treatments simultaneously
Because thousands of patients are randomly assigned across dozens of treatments in parallel, the system collects head-to-head comparative data that would be impossible to generate through sequential RCTs. Within months rather than decades, every treatment can be ranked by measured effectiveness.
Population-specific stratification: RCTs typically exclude 86.1% of patients due to comorbidities, age, or concurrent medications. The narrow populations that qualify cannot support subgroup analysis. Pragmatic trials include all volunteers, generating data on “women over 50 with diabetes” or “patients with genetic marker X.” The filter capability shown above (“Show me effectiveness in women over 50 with my patient’s genetic markers”) is only possible because the underlying data includes those populations.
Outcome Labels
Current drug information: 40-page package inserts written by lawyers, listing every possible side effect without quantifying frequencies. Patients have no idea whether “may cause headaches” means 0.1% or 50% of users.
Standardized outcome labels: Quantified summaries of what actually happens to patients taking each treatment, displayed like nutrition labels:
Based on systematic outcome collection across thousands of patients, labels show:
- Quantified benefits: “Memory improved 35%, Executive Function improved 22%”
- Adverse effect frequencies: “Headache: 9% (8% mild, 1% severe); Fatigue: 7%”
- Treatment persistence: “2.3% discontinued due to side effects”
- Sample size and confidence: “Based on 4,200 patients, 95% CI”
This is measured data from actual patient outcomes, not marketing claims or lawyer-drafted disclaimers.
Implementation workflow: 1. Patient prescribed new treatment → Automatically enrolled in outcome tracking 2. Patient reports symptoms at routine visits → Data flows into aggregation system 3. Lab results, ER visits, prescription refills → Automatically captured from electronic health records 4. System aggregates outcomes across all patients taking that treatment → Updates outcome label in real-time 5. Next doctor/patient looking at that treatment sees current evidence, not 5-year-old clinical trial results
No extra paperwork. No dedicated research staff. Just making routine clinical data actually useful for evidence generation.
Summary of Results
637:1 (95% CI: 569:1-790:1) to 84.8M:1 (95% CI: 46.6M:1-144M:1) ROI
Total Economic Value
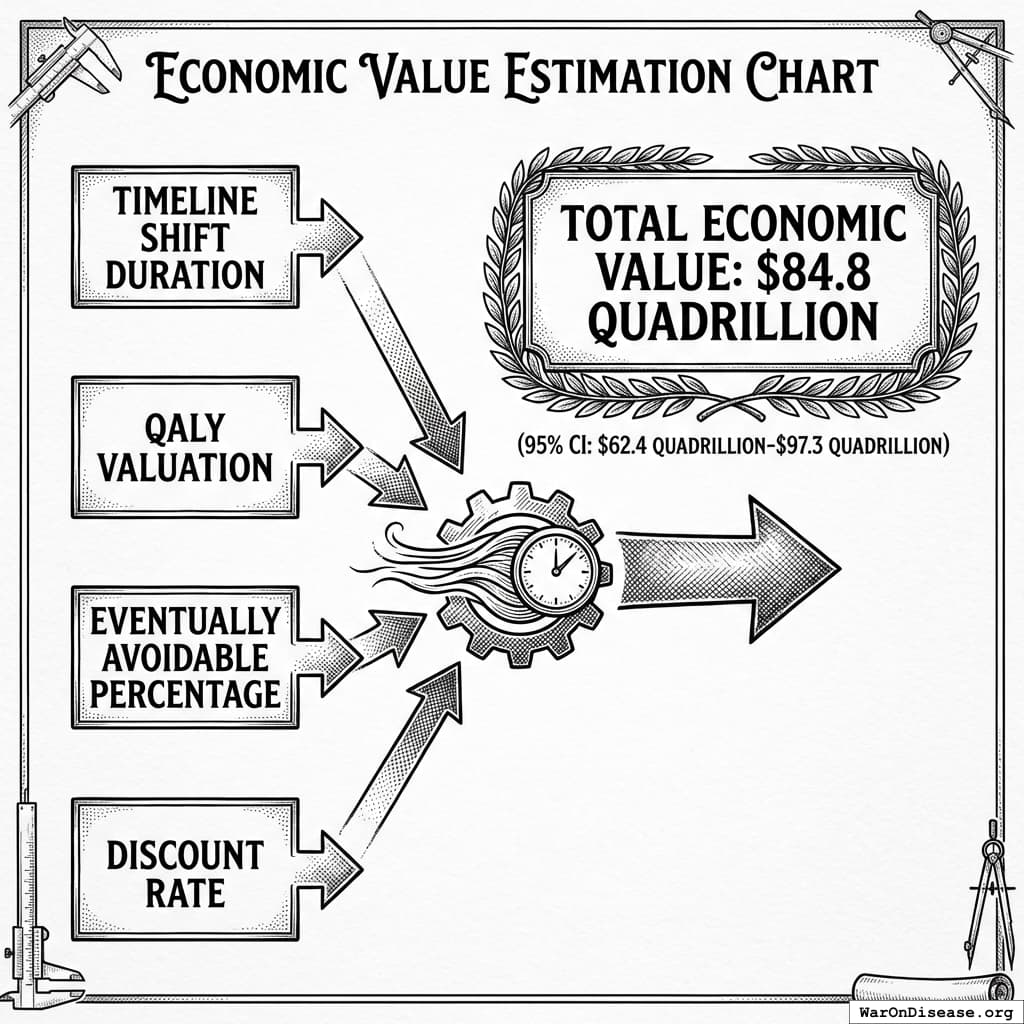
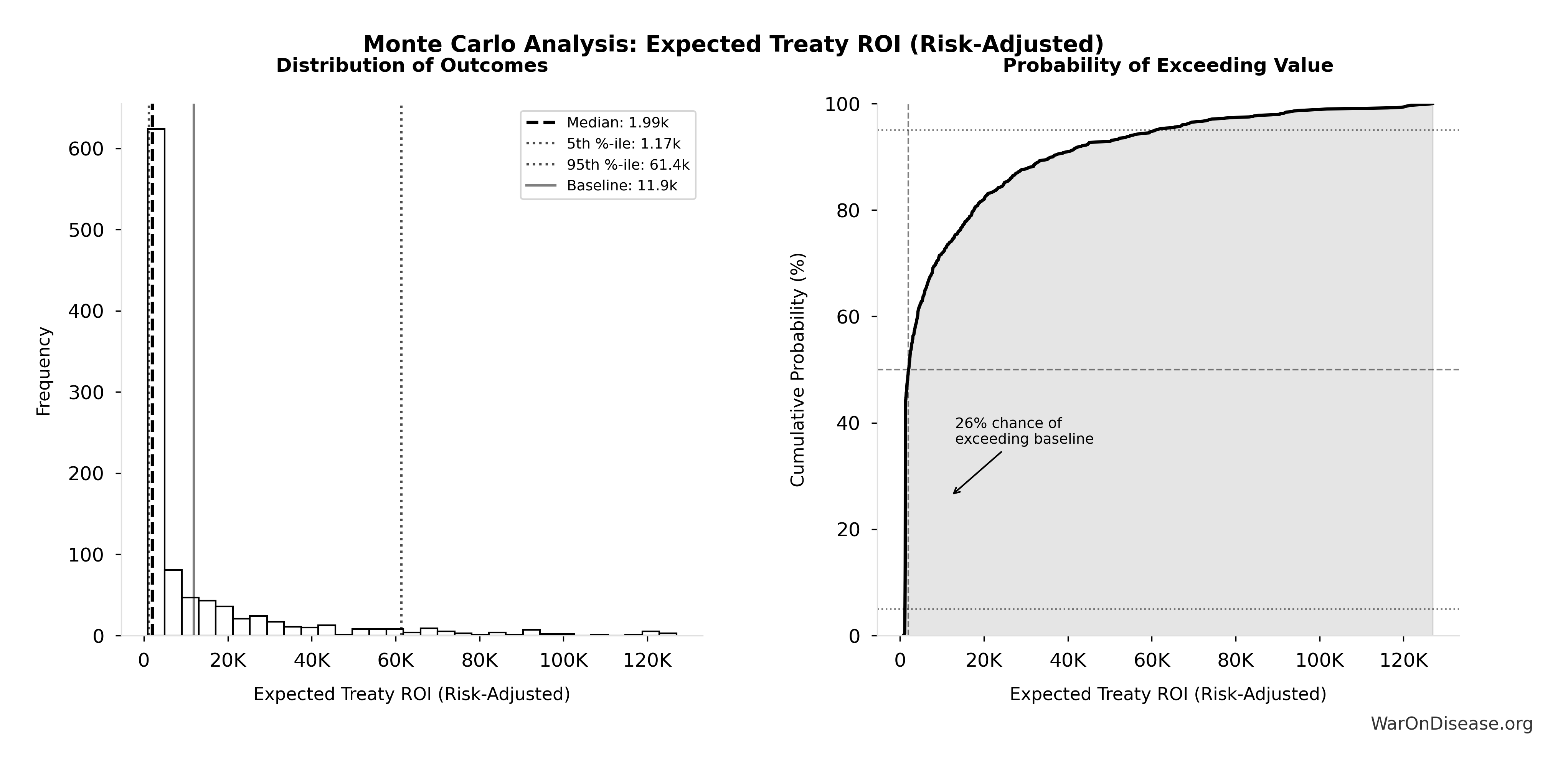
$84.8 quadrillion (95% CI: $62.4 quadrillion-$97.3 quadrillion) in total economic value (cumulative over ~212 years (95% CI: 135 years-355 years) timeline shift, conditional on implementation).
This is the monetized value of 10.7 billion deaths (95% CI: 7.39 billion deaths-16.2 billion deaths) saved and 565 billion DALYs (95% CI: 361 billion DALYs-877 billion DALYs) healthy life-years gained, using standard QALY valuation ($150K (95% CI: $100K-$199K)/QALY). On average, first treatments become available 212 years (95% CI: 135 years-355 years) earlier - combining treatment acceleration (204 years (95% CI: 123 years-350 years) average from expanded trial capacity) and efficacy lag elimination (8.2 years (95% CI: 4.85 years-11.5 years) from deploying treatments once discovered).
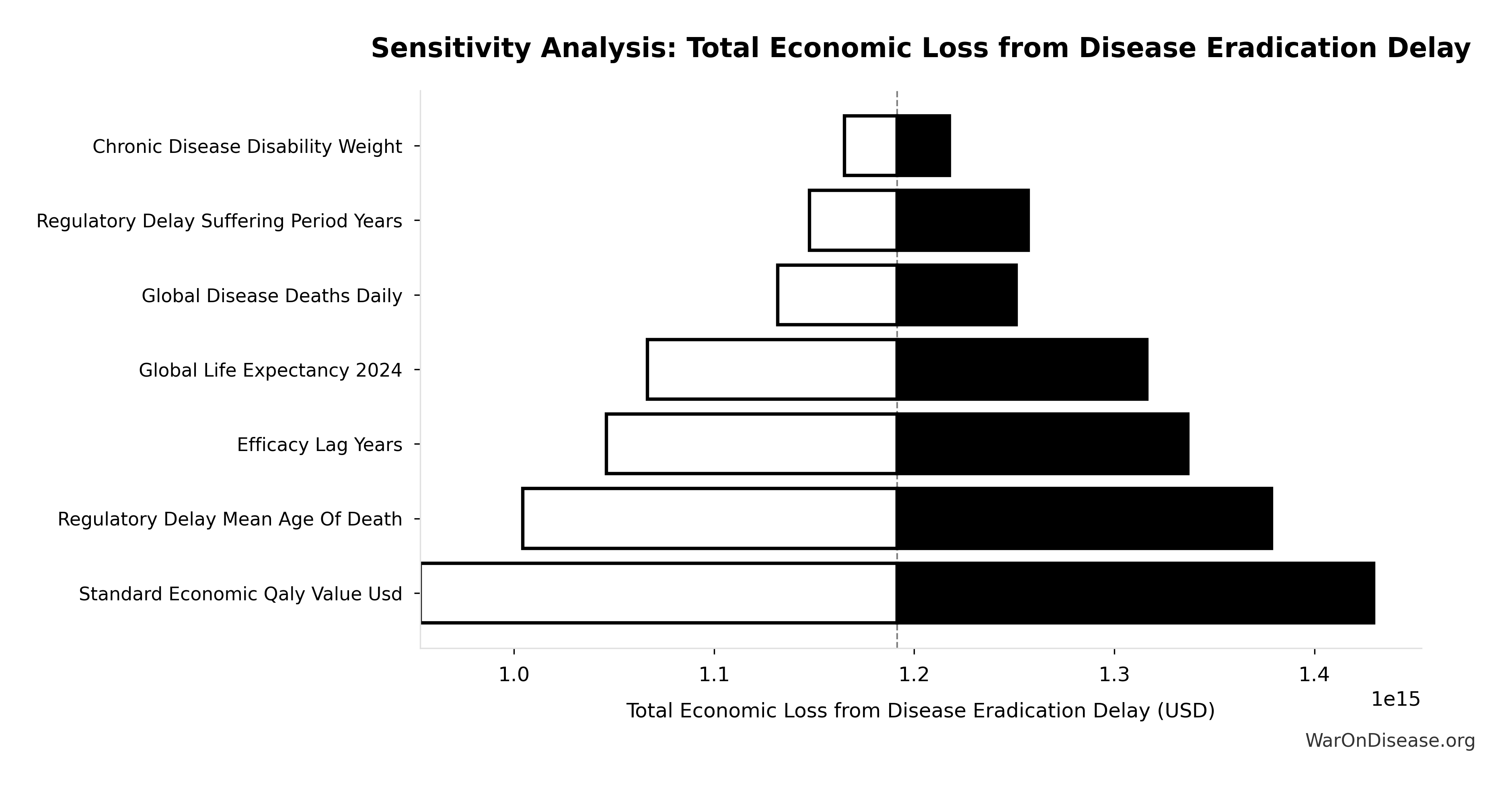
Uncertainty Analysis: Total Economic Value
The tornado diagram shows that timeline shift duration and QALY valuation dominate the uncertainty in total economic value. Even under conservative parameter assumptions, the intervention generates quadrillions in cumulative economic value over the timeline shift period (not annually).
Simulation Results Summary: Total Economic Benefit from Elimination of Efficacy Lag Plus Earlier Treatment Discovery from Higher Trial Throughput
| Baseline (deterministic) |
$84.8 quadrillion |
| Mean (expected value) |
$87.8 quadrillion |
| Median (50th percentile) |
$92.8 quadrillion |
| Standard Deviation |
$11.5 quadrillion |
| 90% Range (5th-95th percentile) |
[$62.4 quadrillion, $97.3 quadrillion] |
The histogram shows the distribution of Total Economic Benefit from Elimination of Efficacy Lag Plus Earlier Treatment Discovery from Higher Trial Throughput across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Monte Carlo analysis confirms the 95% confidence interval for total economic value remains in the quadrillions across all plausible scenarios. These are cumulative values representing accelerated access to treatments over ~212 years (95% CI: 135 years-355 years), not annual benefits.
Investment required: $1B
Lives Saved
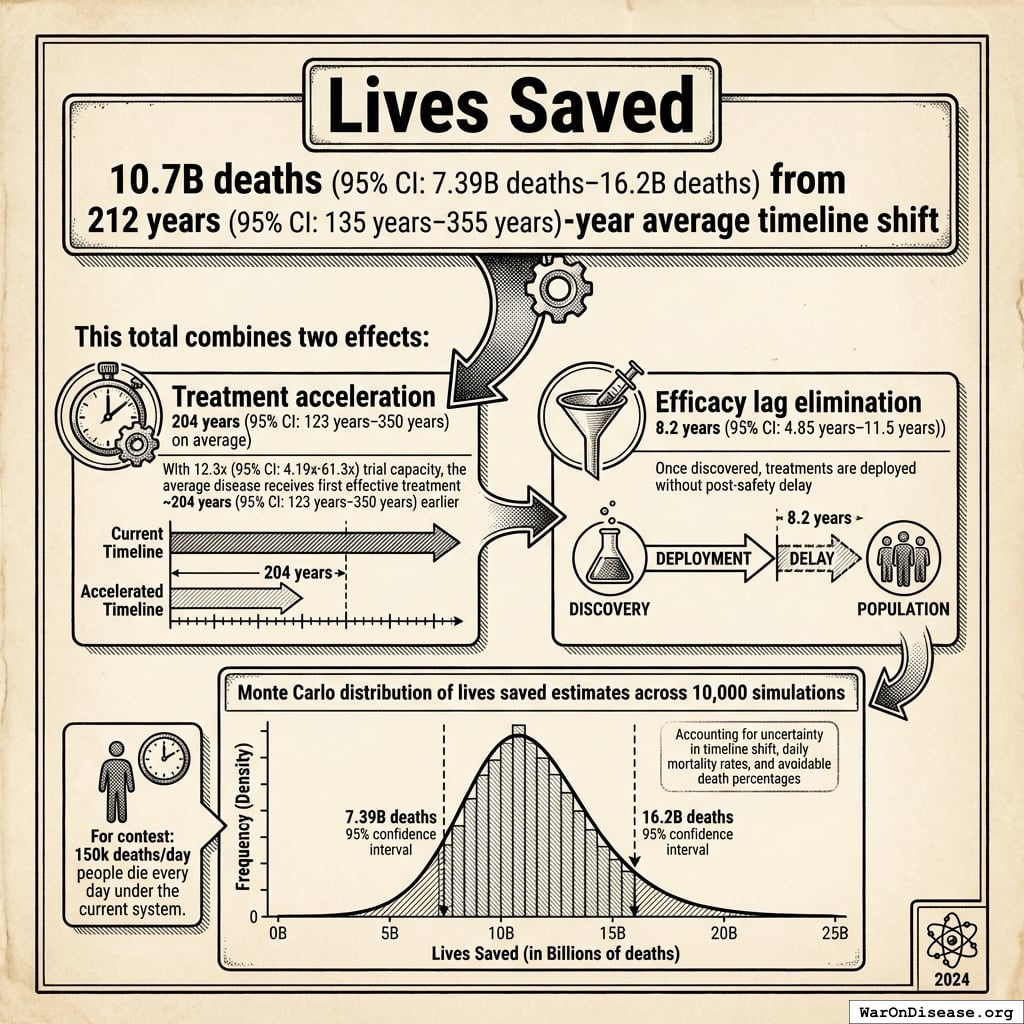
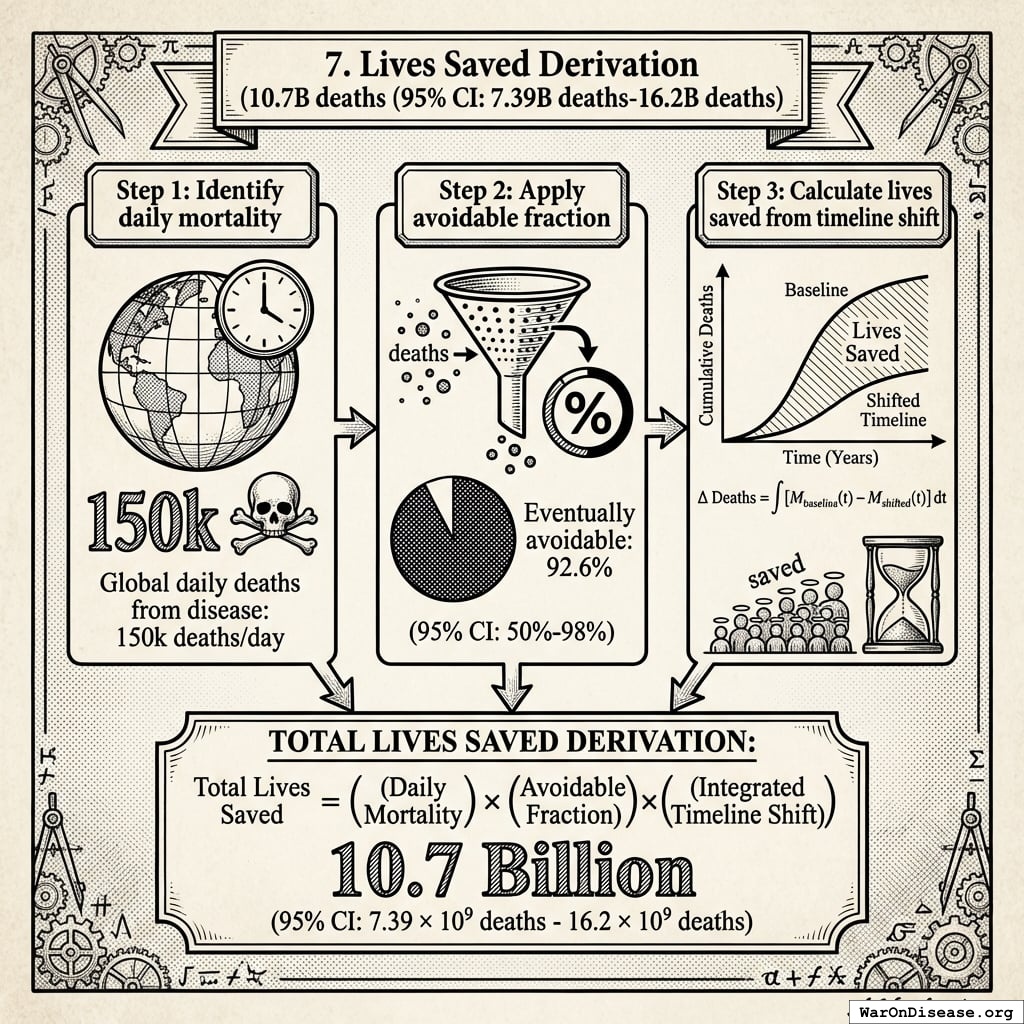
10.7 billion deaths (95% CI: 7.39 billion deaths-16.2 billion deaths) from 212 years (95% CI: 135 years-355 years) average timeline shift
This total combines two effects:
For context: 150 thousand deaths/day people die every day under the current system.
The Monte Carlo distribution below shows the range of lives saved estimates across 10,000 simulations, accounting for uncertainty in timeline shift, daily mortality rates, and avoidable death percentages:
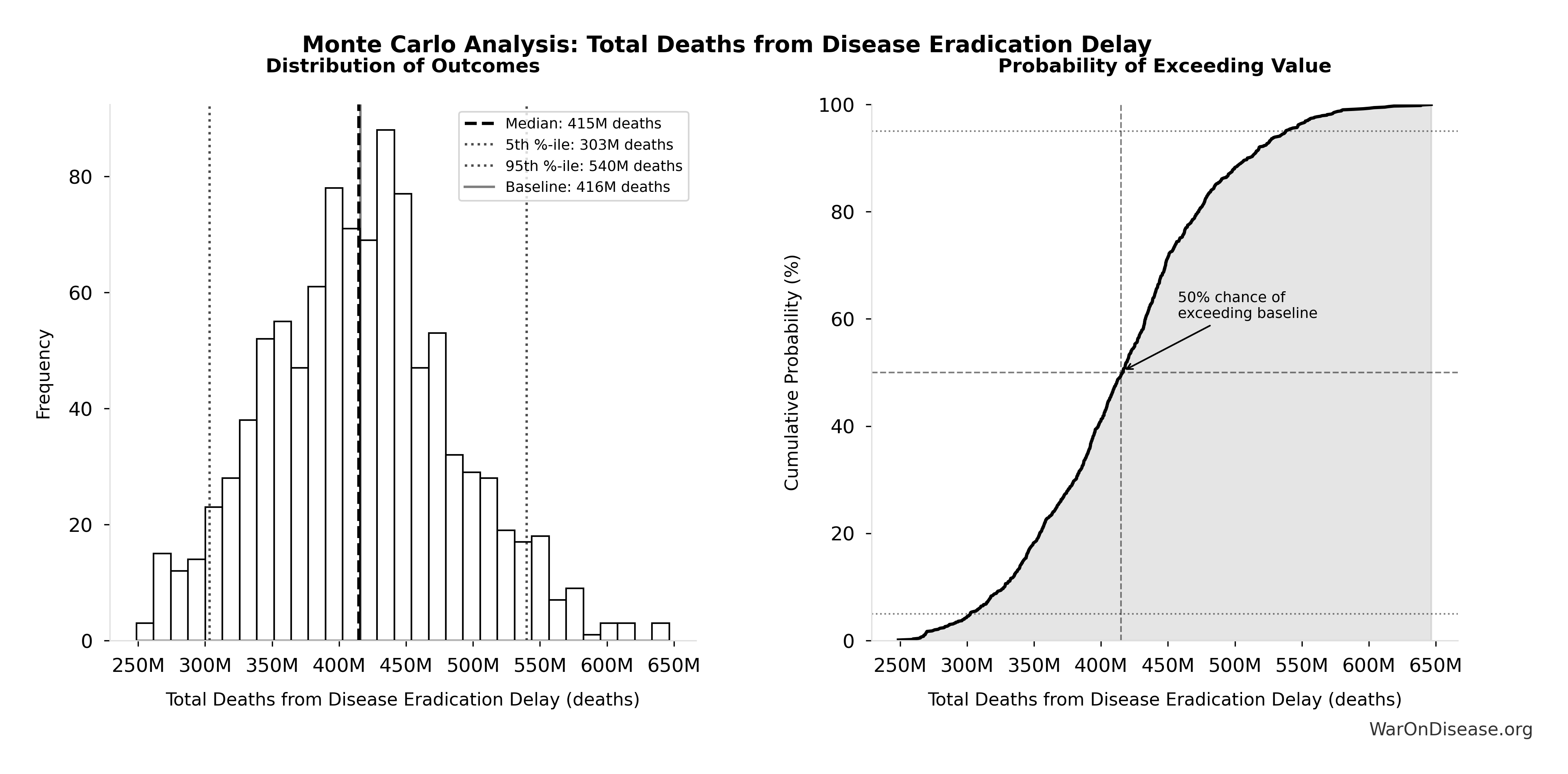
Simulation Results Summary: Total Lives Saved from Elimination of Efficacy Lag Plus Earlier Treatment Discovery from Higher Trial Throughput
| Baseline (deterministic) |
10.7 billion |
| Mean (expected value) |
11.7 billion |
| Median (50th percentile) |
11.7 billion |
| Standard Deviation |
2.45 billion |
| 90% Range (5th-95th percentile) |
[7.39 billion, 16.2 billion] |
The histogram shows the distribution of Total Lives Saved from Elimination of Efficacy Lag Plus Earlier Treatment Discovery from Higher Trial Throughput across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
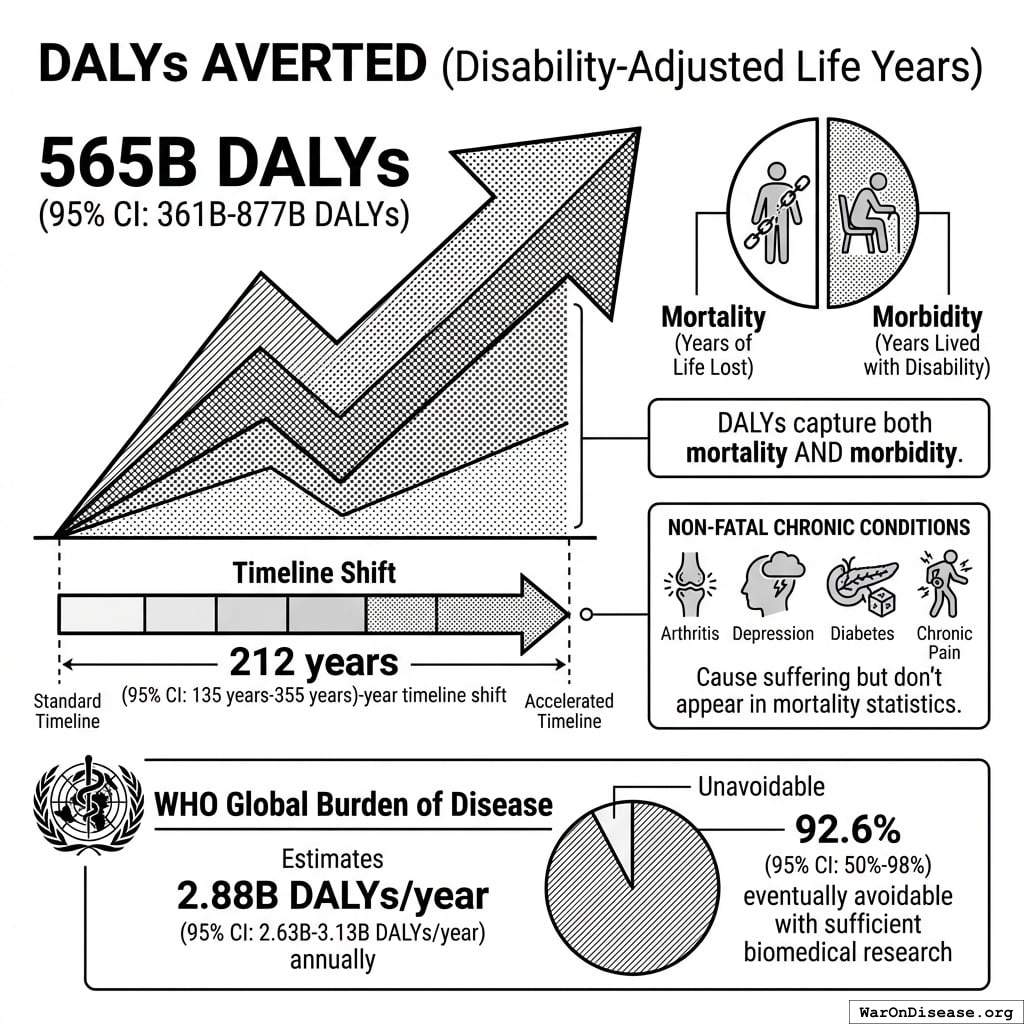
DALYs Averted
565 billion DALYs (95% CI: 361 billion DALYs-877 billion DALYs) (Disability-Adjusted Life Years) averted from the 212 years (95% CI: 135 years-355 years) timeline shift.
DALYs capture both mortality (years of life lost) AND morbidity (years lived with disability). This includes non-fatal chronic conditions like arthritis, depression, diabetes, and chronic pain that cause suffering but don’t appear in mortality statistics. The WHO Global Burden of Disease estimates 2.88 billion DALYs/year (95% CI: 2.63 billion DALYs/year-3.13 billion DALYs/year) annually, of which 92.6% (95% CI: 50%-98%) are eventually avoidable with sufficient biomedical research.
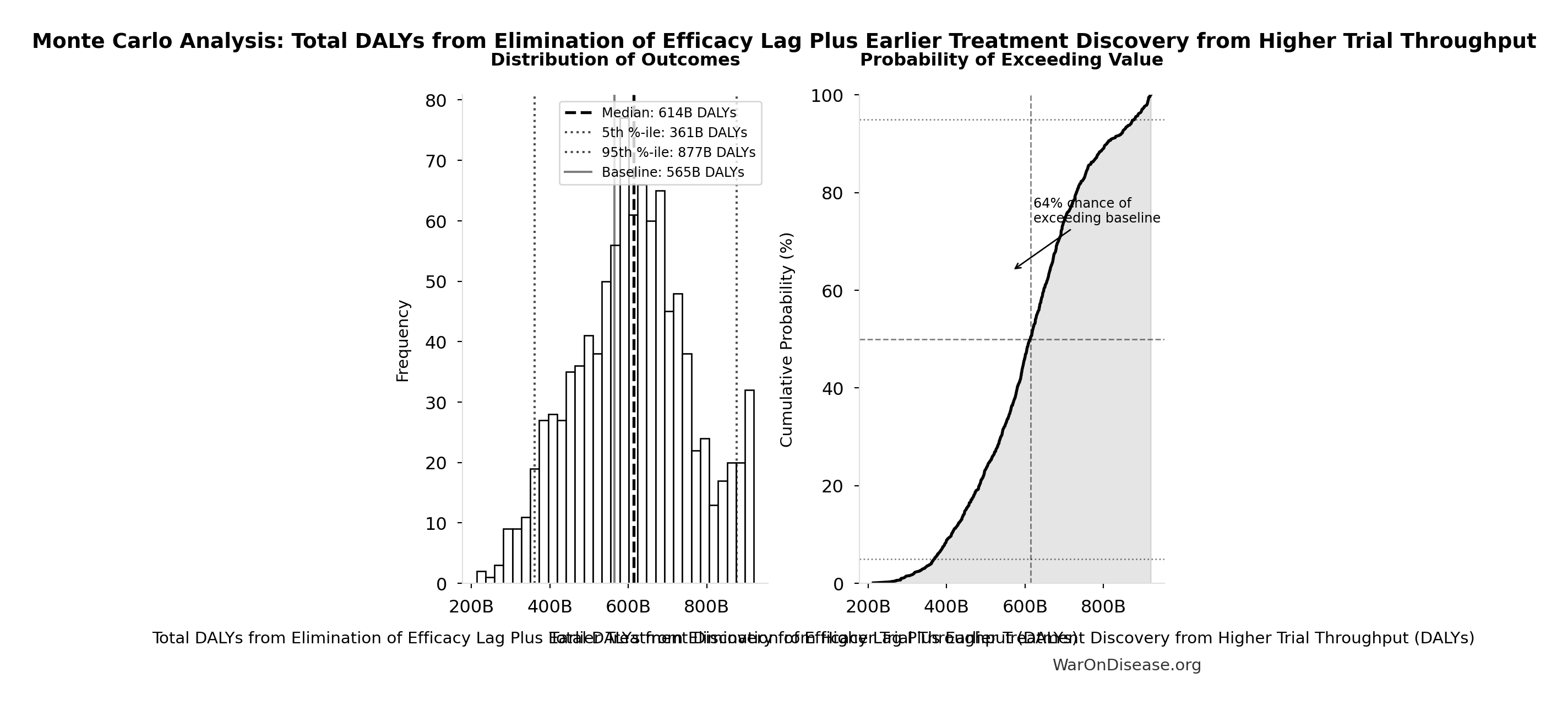
Simulation Results Summary: Total DALYs from Elimination of Efficacy Lag Plus Earlier Treatment Discovery from Higher Trial Throughput
| Baseline (deterministic) |
565 billion |
| Mean (expected value) |
610 billion |
| Median (50th percentile) |
614 billion |
| Standard Deviation |
148 billion |
| 90% Range (5th-95th percentile) |
[361 billion, 877 billion] |
The histogram shows the distribution of Total DALYs from Elimination of Efficacy Lag Plus Earlier Treatment Discovery from Higher Trial Throughput across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Why “Eventually Avoidable” Matters
Of 150 thousand deaths/day:
- 92.6% (95% CI: 50%-98%) eventually avoidable with sufficient biomedical research (gene therapy, AI drug discovery, cellular reprogramming, etc.)
- 7.37% fundamentally unavoidable (primarily accidents, even with advanced prevention)
This differs from “currently preventable” deaths (20-30M annually via vaccines, sanitation, behavior change). The 92.6% (95% CI: 50%-98%) figure represents maximum achievable with advanced biotechnology over decades, not current interventions.
The lives saved calculation measures timeline acceleration, not current curability. With the framework’s 12.3x (95% CI: 4.19x-61.3x) trial capacity increase, the average disease receives first treatment ~204 years (95% CI: 123 years-350 years) earlier. Additionally, eliminating the 8.2 years (95% CI: 4.85 years-11.5 years) efficacy lag means proven treatments reach patients immediately. This logic applies on average across diseases: some first treatments arrive much sooner (early in the therapeutic search space), others somewhat later (later in exploration), with 204 years (95% CI: 123 years-350 years) being the average acceleration.
The Leverage Mechanism: Why 1% Is Enough
The protocol exploits two structural inefficiencies in global capital allocation:
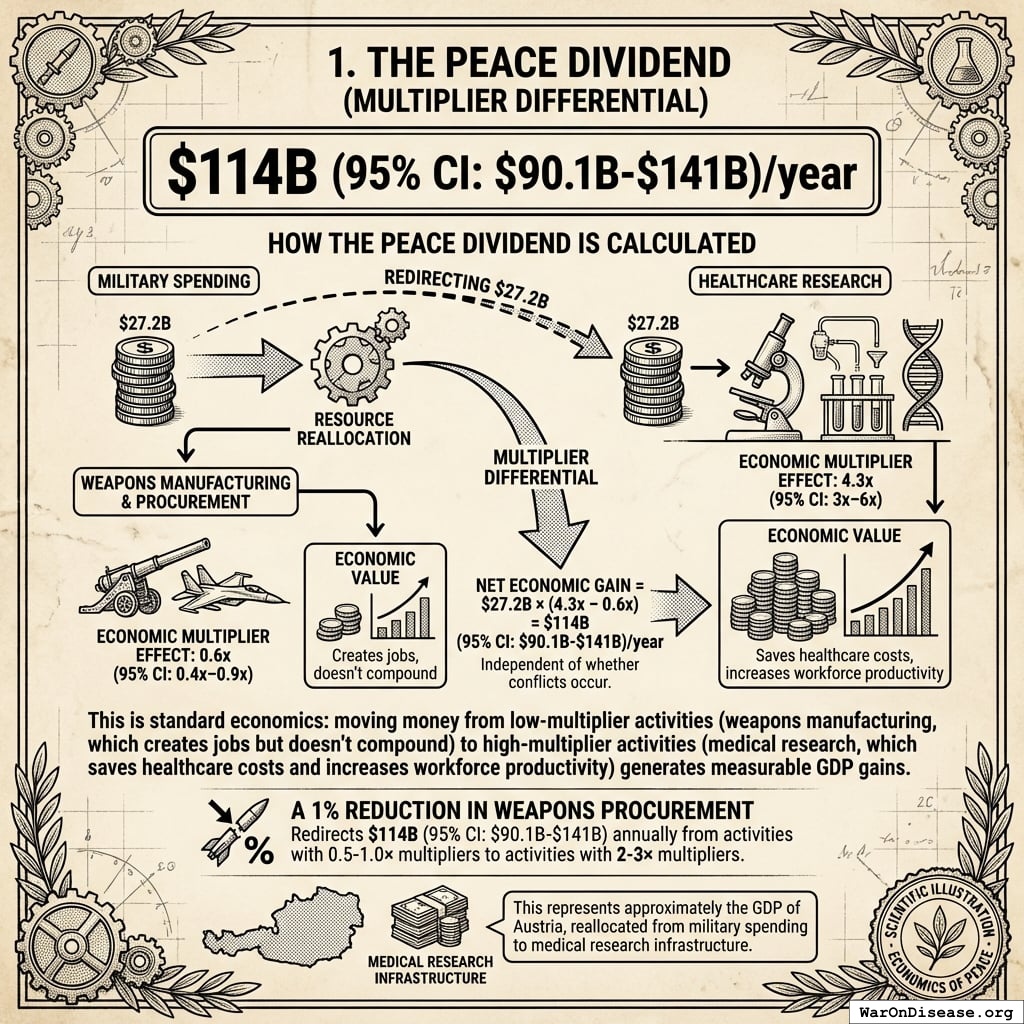
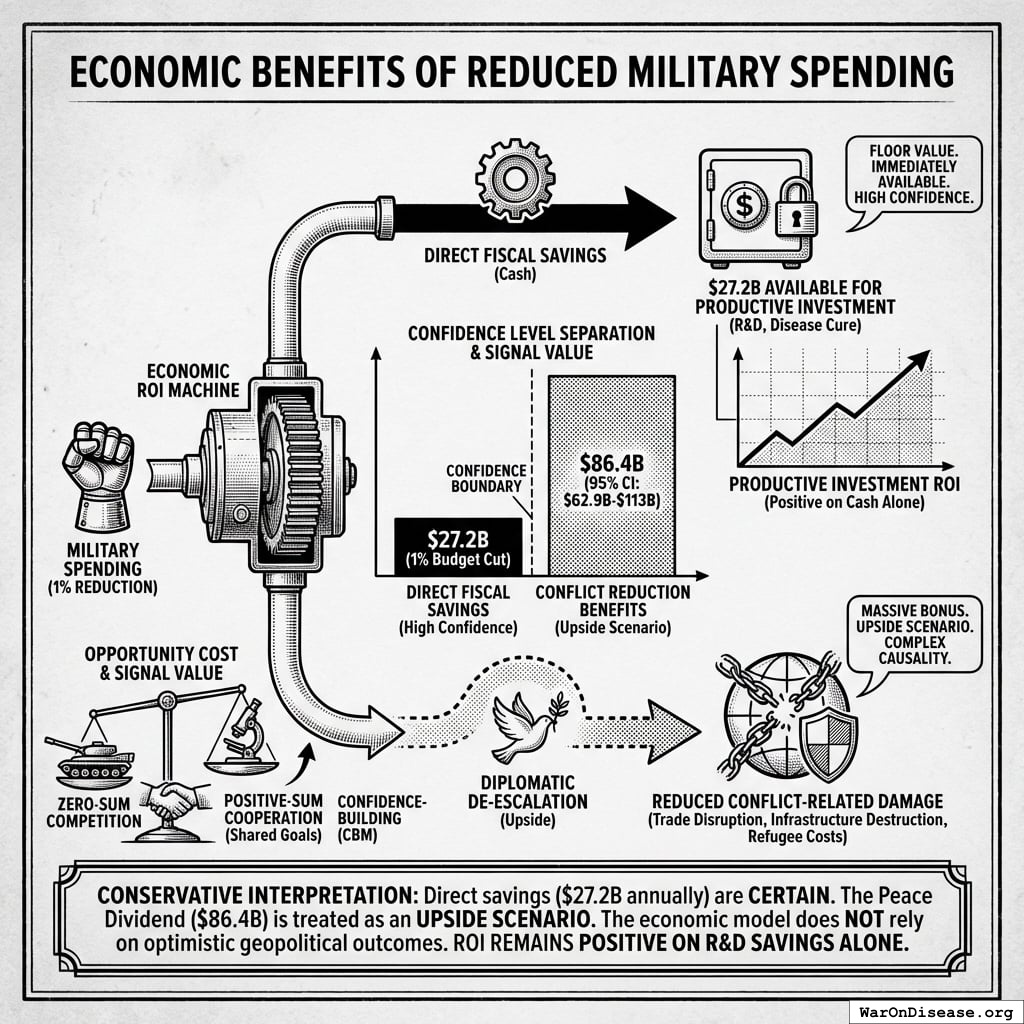
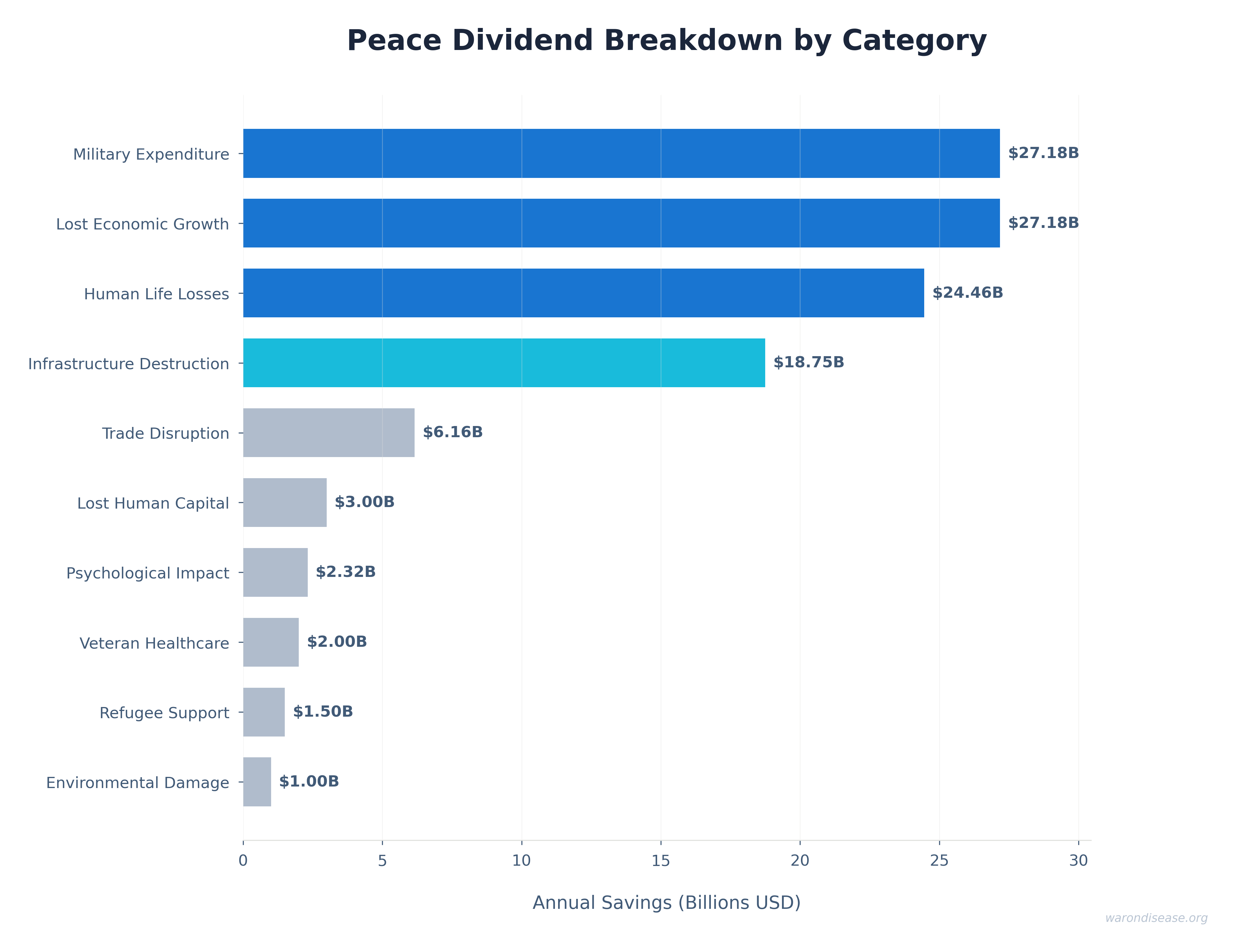
The Peace Dividend (Multiplier Differential)
$114B (95% CI: $90.1B-$141B)/year
How the peace dividend is calculated:
The peace dividend doesn’t assume the treaty prevents wars. It’s based on the economic multiplier effect of resource reallocation: military spending generates 0.6x (95% CI: 0.4x-0.9x) in economic value per dollar spent, while healthcare research generates 4.3x (95% CI: 3x-6x) per dollar. Redirecting $27.2B from military to medical research produces a net economic gain of $114B (95% CI: $90.1B-$141B)/year simply from the multiplier differential, independent of whether conflicts occur.
This is standard economics: moving money from low-multiplier activities (weapons manufacturing, which creates jobs but doesn’t compound) to high-multiplier activities (medical research, which saves healthcare costs and increases workforce productivity) generates measurable GDP gains.
A 1% reduction in weapons procurement redirects $114B (95% CI: $90.1B-$141B) annually from activities with 0.5-1.0× multipliers to activities with 2-3× multipliers. This represents approximately the GDP of Austria, reallocated from military spending to medical research infrastructure.
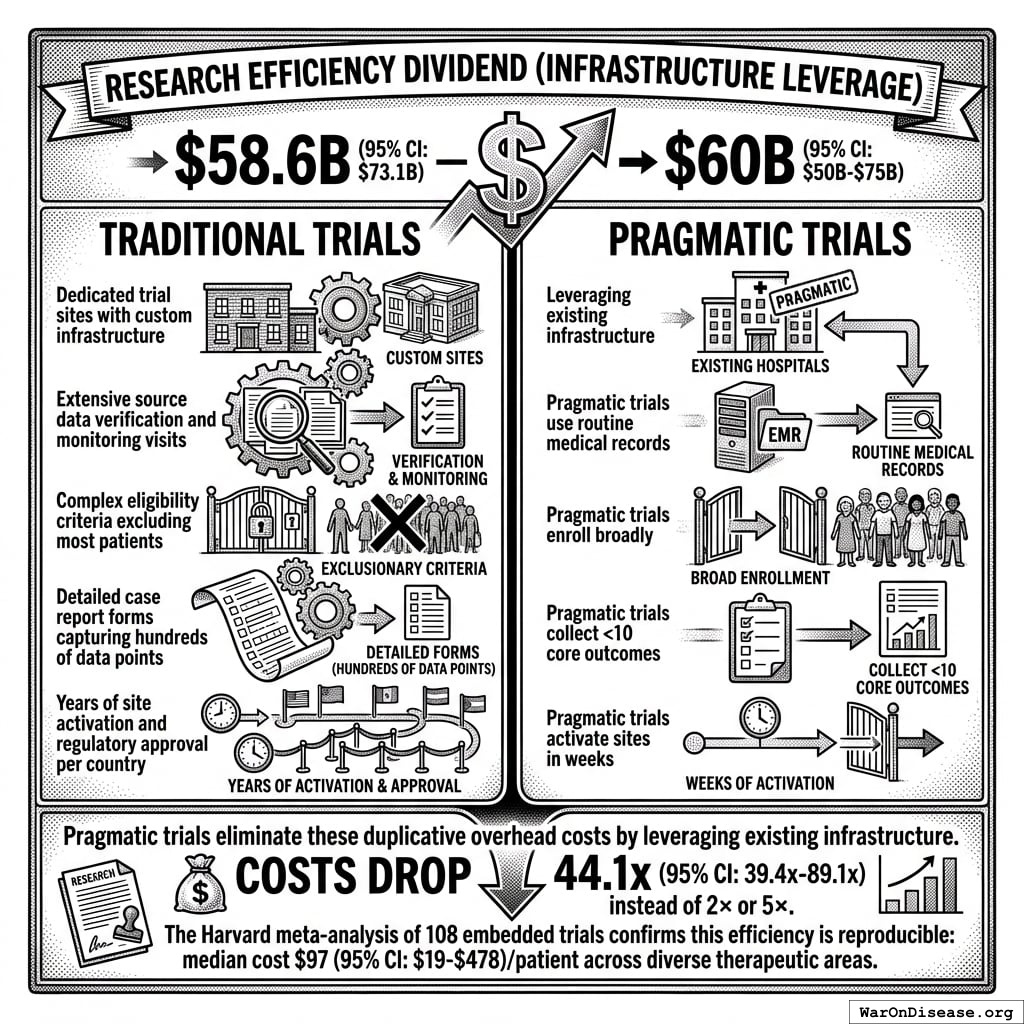
Research Efficiency Dividend (Infrastructure Leverage)
$58.6B (95% CI: $49.2B-$73.1B)–$60B (95% CI: $50B-$75B)42
Traditional trials require:
- Dedicated trial sites with custom infrastructure (pragmatic trials use existing hospitals)
- Extensive source data verification and monitoring visits (pragmatic trials use routine medical records)
- Complex eligibility criteria excluding most patients (pragmatic trials enroll broadly)
- Detailed case report forms capturing hundreds of data points (pragmatic trials collect <10 core outcomes)
- Years of site activation and regulatory approval per country (pragmatic trials activate sites in weeks)
Pragmatic trials eliminate these duplicative overhead costs by leveraging existing infrastructure. The Harvard meta-analysis of 108 embedded trials132 confirms this efficiency is reproducible: median cost $97 (95% CI: $19-$478)/patient across diverse therapeutic areas. This structural difference explains why costs drop 44.1x (95% CI: 39.4x-89.1x) instead of 2× or 5×.
15–40 “NIH equivalents” of new research capacity
Currently, diseases kill people faster than we develop effective treatments. This would change that.
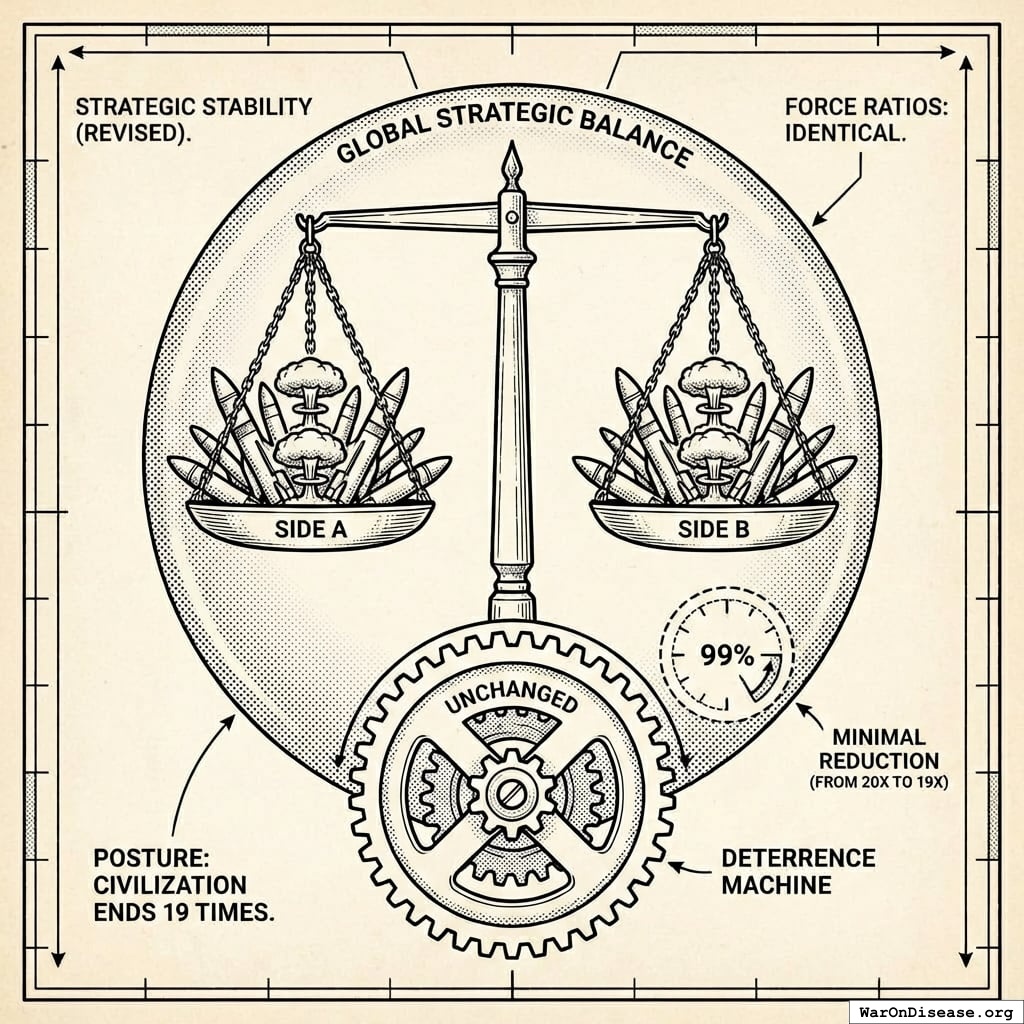
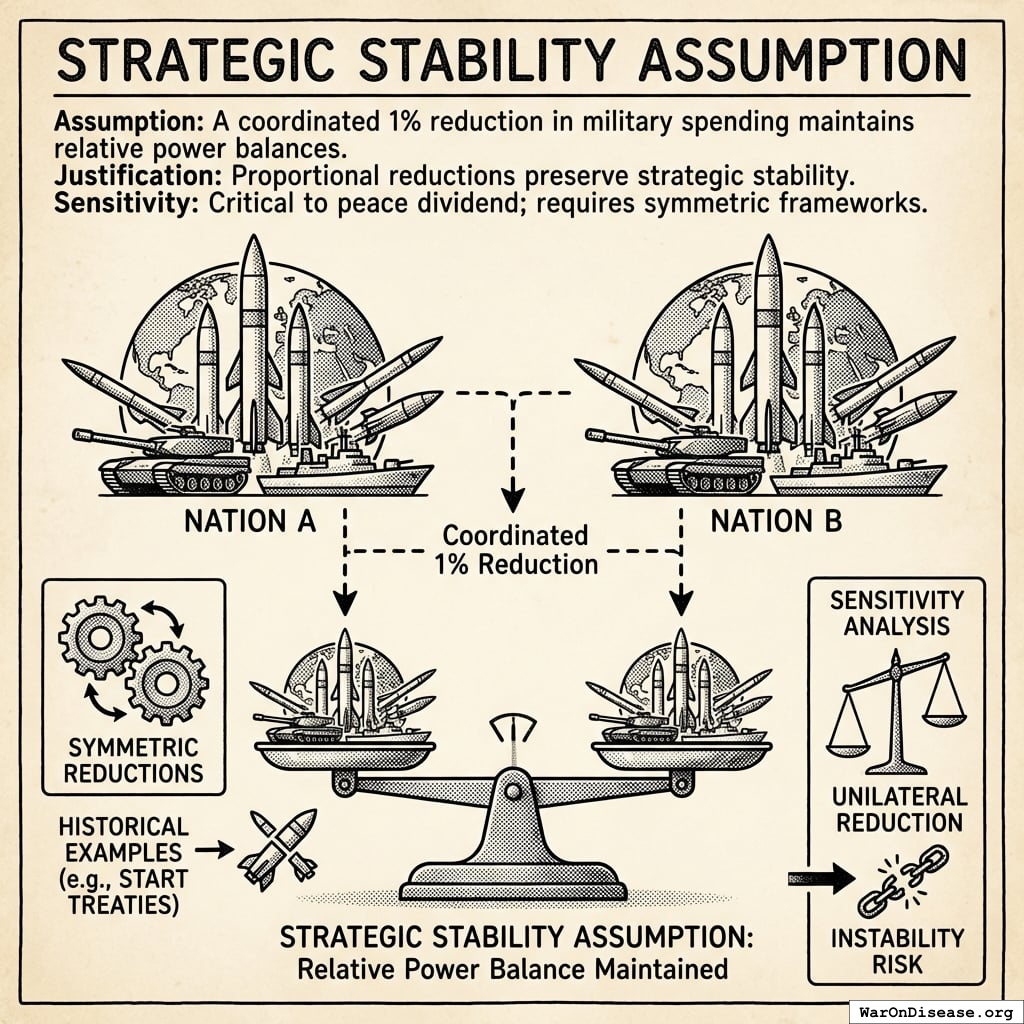
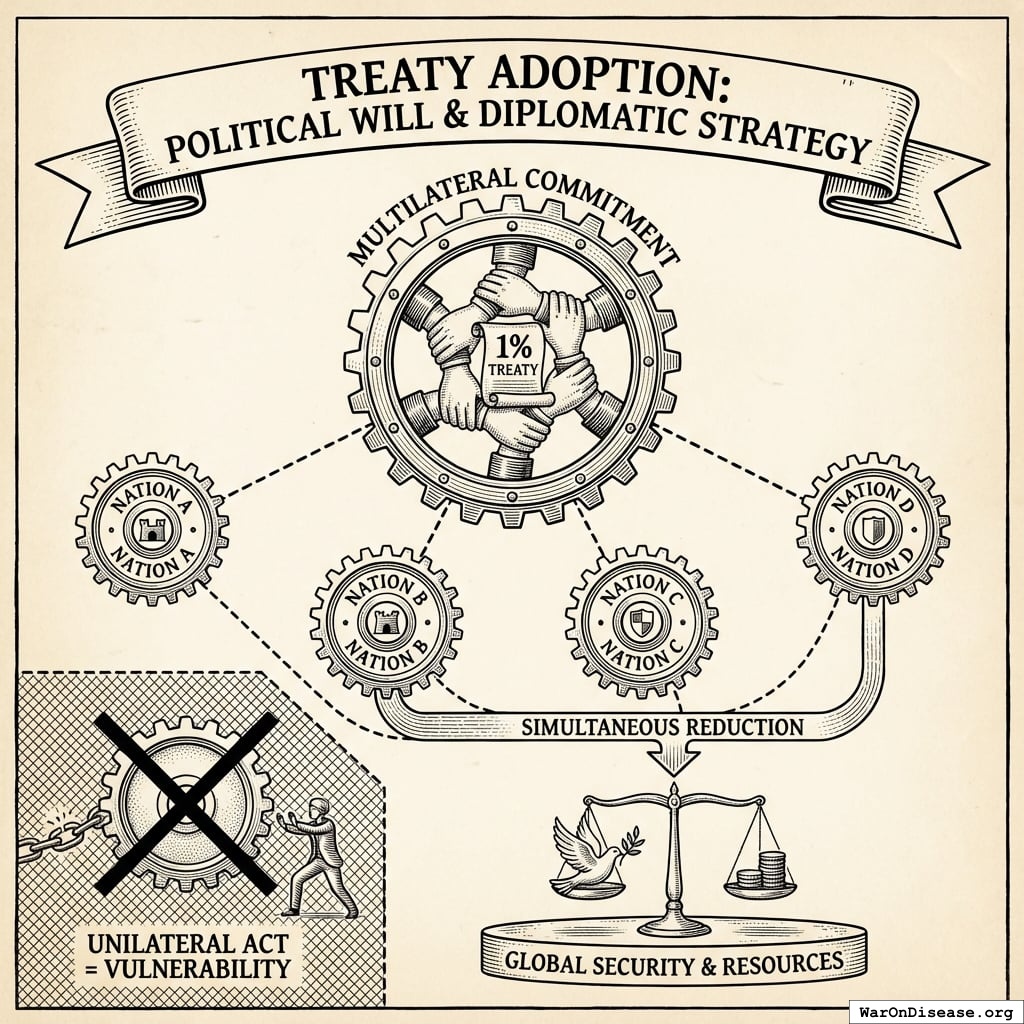
How It Increases National Security
All signatories reduce by 1% simultaneously.
What doesn’t change
- Power balances (everyone cuts equally)
- Deterrence (still plenty of weapons)
- Force ratios (relative strength identical)
- Strategic stability (same as before, just 1% less apocalyptic)
- Nuclear posture (can still end civilization 19 times instead of 20)
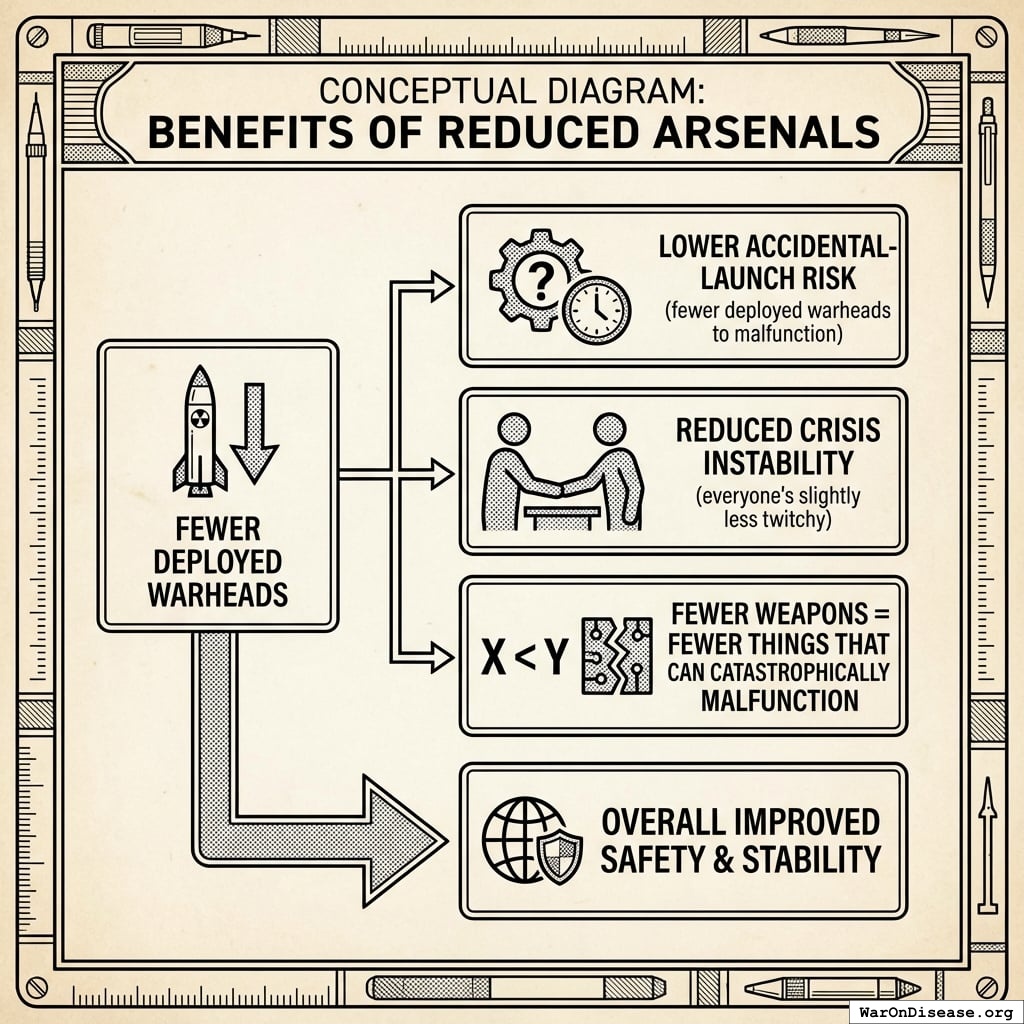
What improves
- Fewer deployed warheads (less probability someone launches by mistake)
- Lower accidental-launch risk (fewer deployed warheads to malfunction)
- Reduced crisis instability (everyone’s slightly less twitchy)
- Fewer weapons = fewer things that can catastrophically malfunction
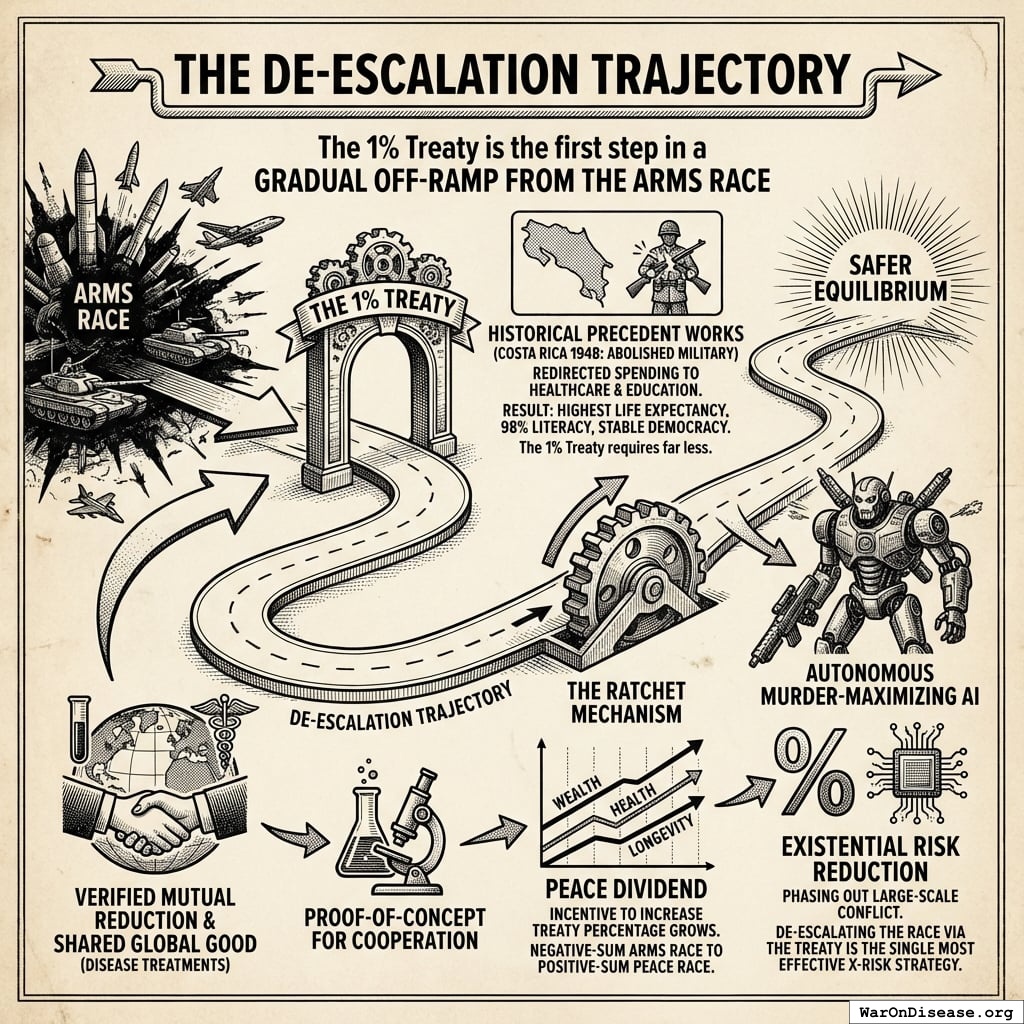
The De-escalation Trajectory
The 1% Treaty is the first step in a gradual off-ramp from the arms race.
By successfully executing a verified, mutual reduction in military spending to fund a shared global good (developing disease treatments), humanity establishes a proof-of-concept for cooperation.
- Historical precedent works: Costa Rica abolished its military entirely in 1948, redirecting defense spending to universal healthcare and education. Result: highest life expectancy in Central America (80 years), 98% literacy, and stable democracy for 75+ years. The 1% Treaty requires far less. It maintains virtually all military capacity while redirecting just 1% to health research.
- The Ratchet Mechanism: Once the economic benefits of the “Peace Dividend” (wealth, health, longevity) materialize, the incentive to increase the treaty percentage grows. We move from a negative-sum arms race to a positive-sum “peace race.”
- Existential Risk Reduction: Gradually increasing the percentage creates a trajectory toward phasing out large-scale conflict entirely. Since a primary driver of existential risk is autonomous murder-maximizing AI produced by military arms races, de-escalating this race via the treaty is arguably the single most effective X-Risk strategy available.
This gradual approach steers nations toward a safer equilibrium, one percentage point at a time.
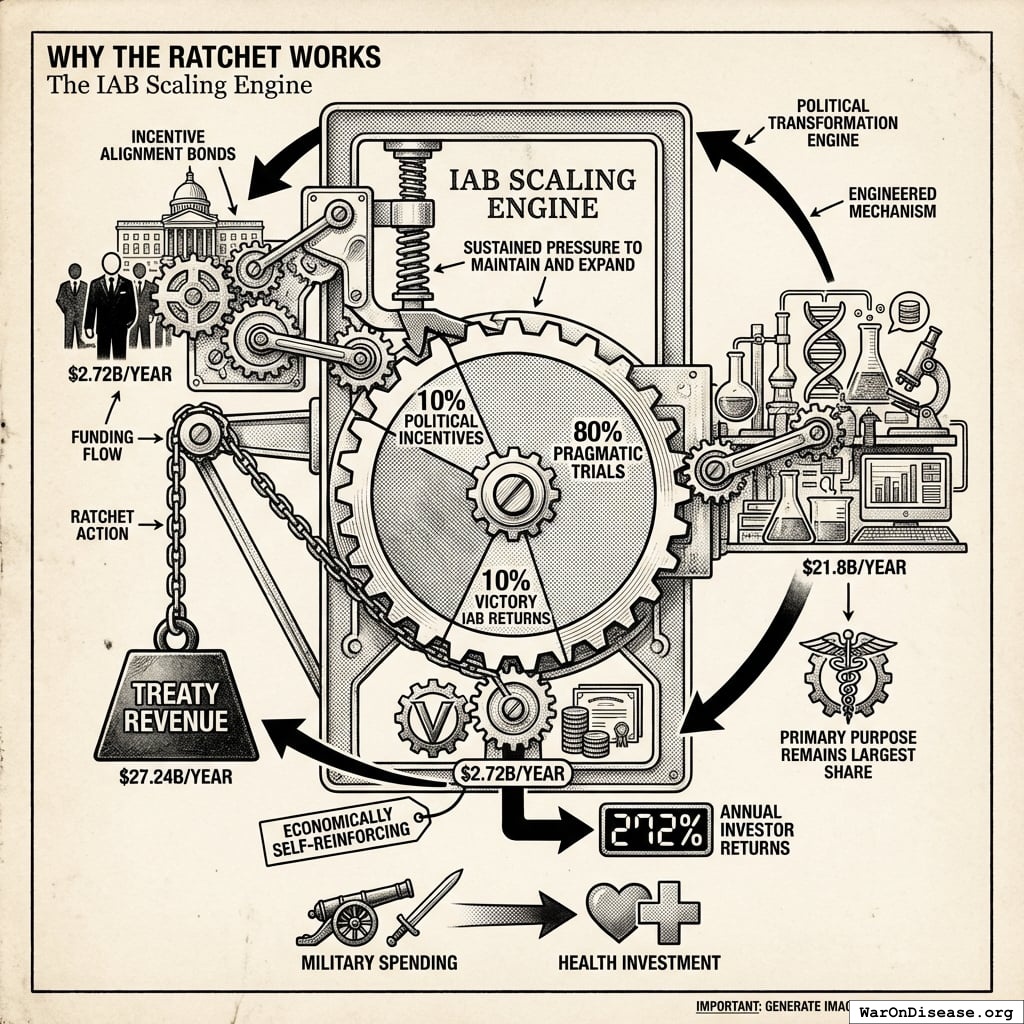
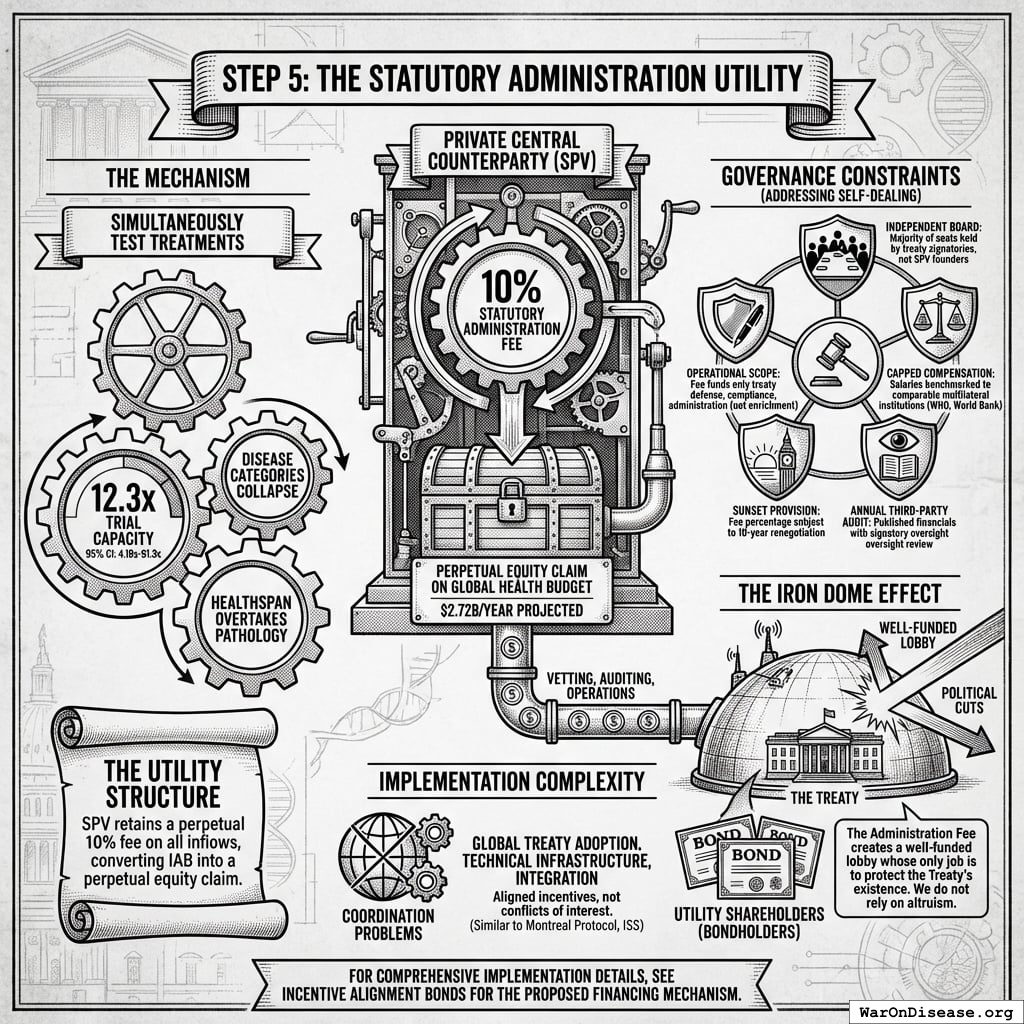
Why The Ratchet Works: The IAB Scaling Engine
The ratchet mechanism isn’t just economic gravity. It’s engineered through Incentive Alignment Bonds.
The mechanism: 10% of treaty revenue ($2.72B/year) funds political incentives while 80% ($21.8B/year) funds pragmatic trials. The remaining 10% funds Incentive Alignment Bond investor returns.
Incentive Alignment Bond investors receive projected 272% on their investment. The 10% allocation to political incentives creates sustained pressure to maintain and expand the treaty, while the 80% allocation ensures the primary purpose (funding pragmatic trials) remains the largest share.
This allocation structure (80% medical research, 10% investor returns, 10% political incentives) functions as a political transformation engine, making the transition from military spending to health investment economically self-reinforcing.
Political Economy and Financing
Ideas don’t win on merit alone. They win by aligning incentives.
This section describes how Incentive Alignment Bonds (IABs) restructure the political economy of global health funding.
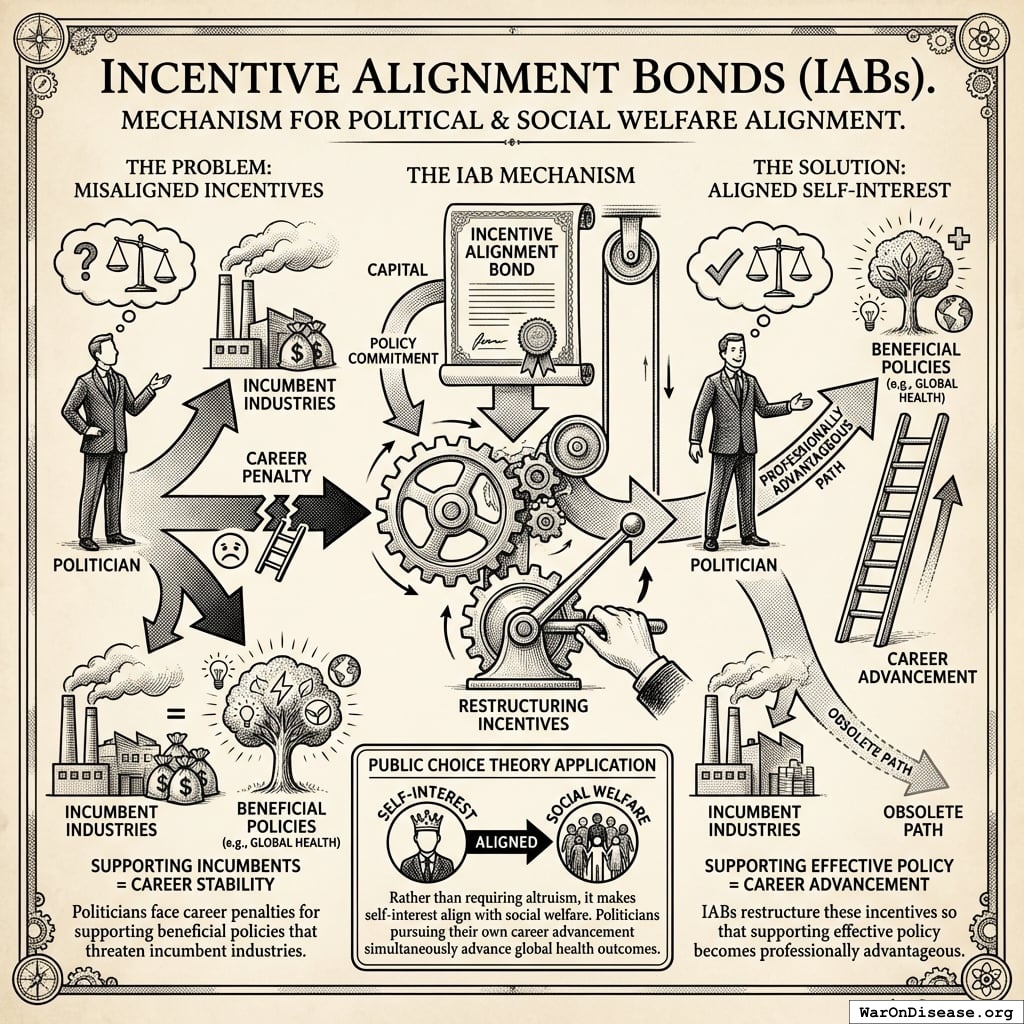
Incentive Alignment Bonds
Incentive Alignment Bonds address a fundamental problem: politicians face career penalties for supporting beneficial policies that threaten incumbent industries. IABs restructure these incentives so that supporting effective policy becomes professionally advantageous.
The mechanism applies public choice theory systematically. Rather than requiring altruism, it makes self-interest align with social welfare. Politicians pursuing their own career advancement simultaneously advance global health outcomes.
Mechanism Architecture
Politicians are evaluated through a Public Good Score based on verifiable voting records for treaty funding. This scoring system creates three channels of incentive alignment:
- Electoral advantage: Independent campaign support flows to high-scoring politicians
- Reputational benefits: Public scores create transparency and accountability
- Post-office opportunities: High scorers gain access to prestigious fellowships, advisory positions, and speaking engagements
Critically, no direct monetary transfers to politicians occur. Benefits flow through reputation, electoral support, and career advancement - all based on publicly verifiable voting records that cannot be manipulated.
Comparative Static Analysis: Senator Smith
Consider a legislator’s decision calculus regarding the 1% Treaty vote:
Without IABs:
| Vote Yes |
Military lobby attack ads; reduced industry support |
| Vote No |
Retained military contractor funding; no electoral risk |
With IABs:
| Vote Yes |
Public Good Score: 45 → 72; P(reelection): 55% → 62%; Expected post-office income: $200K → $500K/yr |
| Vote No |
Score: 45 → 30; P(reelection): 55% → 48%; Opposition receives $2M independent support |
The mechanism changes the math. Supporting beneficial policy becomes professionally advantageous rather than requiring self-sacrifice.
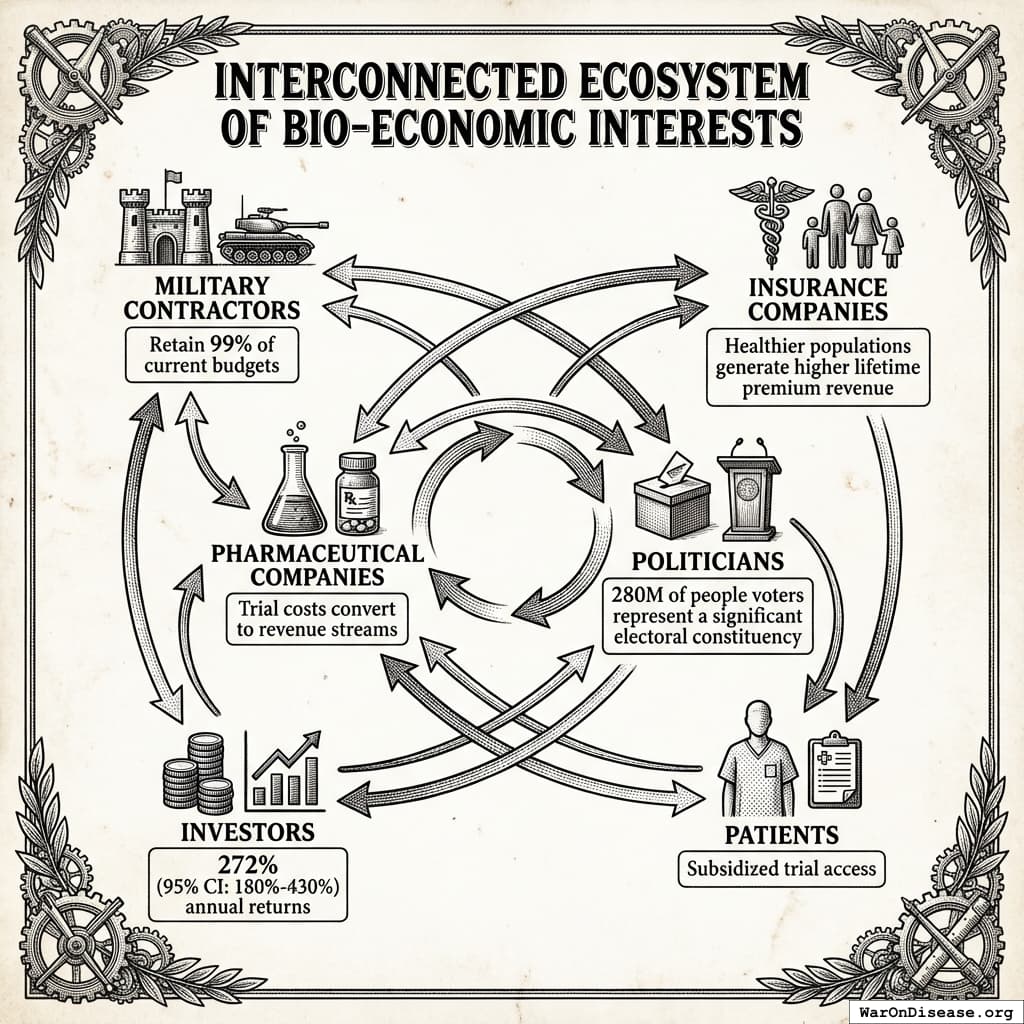
Stakeholder Alignment
The IAB mechanism aligns incentives across all key stakeholder groups:
Military Contractors: Retain 99% of current budgets while earning projected 272% returns on Incentive Alignment Bonds. The treaty creates new revenue streams without threatening core business.
Insurance Companies: Healthier populations generate higher lifetime premium revenue. Patients living longer with better health outcomes produce better actuarial performance than the current mortality-driven model.
Pharmaceutical Companies: Trial costs convert to revenue streams. Instead of paying $41K (95% CI: $20K-$120K)101 per trial patient, companies collect $929 (95% CI: $97-$3K)1 subsidies when patients enroll. This transforms trials from cost centers to profit centers.
Politicians: 280 million of people voters represent a significant electoral constituency. Politicians supporting the treaty gain reputation benefits, campaign support, and reduced opposition funding. Those opposing it face well-funded challengers and organized voter blocs.
\[
\begin{gathered}
N_{voters,target} \\
= Pop_{global} \times Threshold_{activism} \\
= 8B \times 3.5\% \\
= 280M
\end{gathered}
\]
Investors: Incentive Alignment Bonds offer projected 272%, substantially exceeding typical market returns of 10%.
\[
\begin{gathered}
r_{bond} \\
= \frac{Payout_{bond,ann}}{Cost_{campaign}} \\
= \frac{\$2.72B}{\$1B} \\
= 272\%
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{campaign} \\
= Budget_{viral,base} + Budget_{lobby,treaty} \\
+ Budget_{reserve} \\
= \$250M + \$650M + \$100M \\
= \$1B
\end{gathered}
\]
Patients: Subsidized access to experimental treatments recommended by physicians. Patients choose which trials to join, with subsidies following their decisions. Additional benefits include lifetime wealth gains and longevity increases from the economic multiplier effect.
The mechanism redirects competitive incentives from zero-sum conflicts toward positive-sum health outcomes.
See Aligning Incentives for complete analysis.
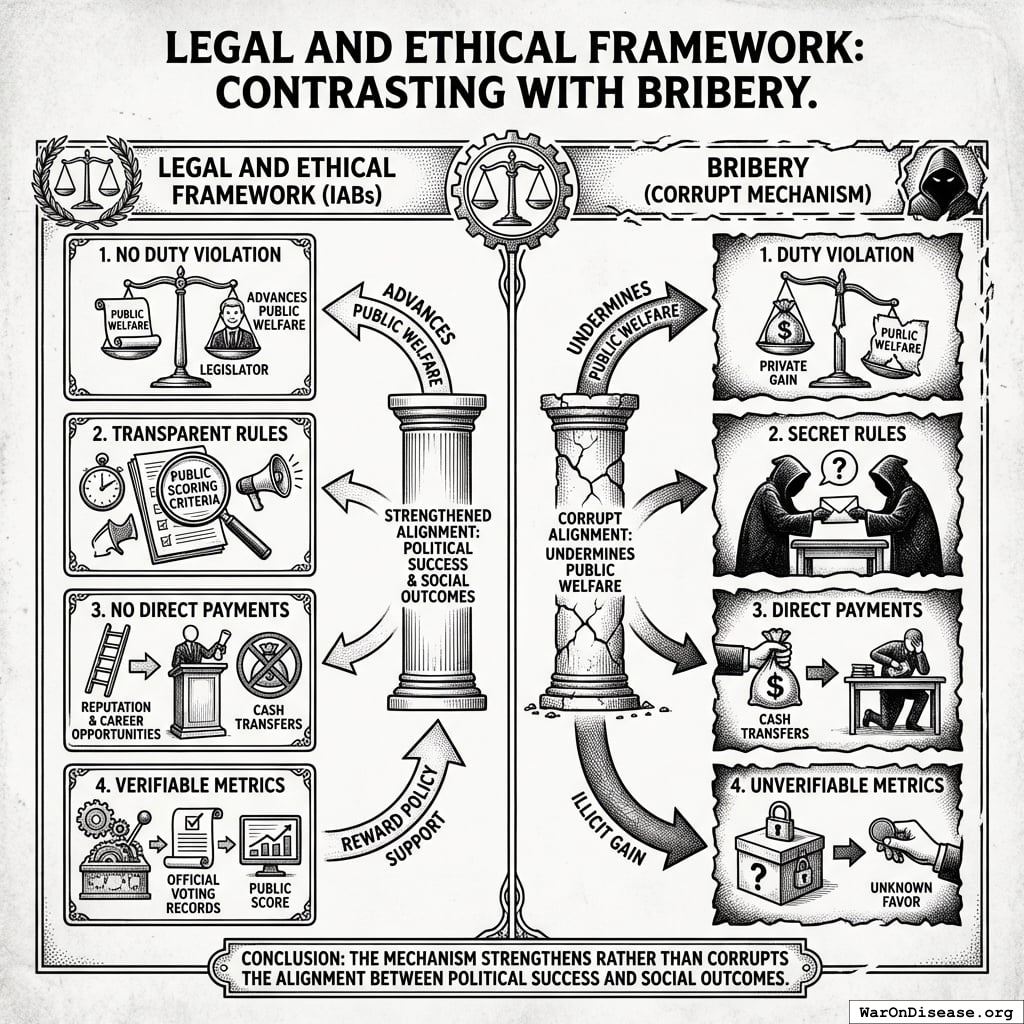
Legal and Ethical Framework
This mechanism differs from bribery in four key ways:
- No duty violation: IABs reward policy support that advances rather than undermines public welfare
- Transparent rules: Scoring criteria are public, announced in advance, and apply equally to all legislators
- No direct payments: Benefits flow through reputation, electoral support, and career opportunities, not cash transfers
- Verifiable metrics: Scores depend entirely on public voting records from official government sources
The mechanism strengthens rather than corrupts the alignment between political success and social outcomes.
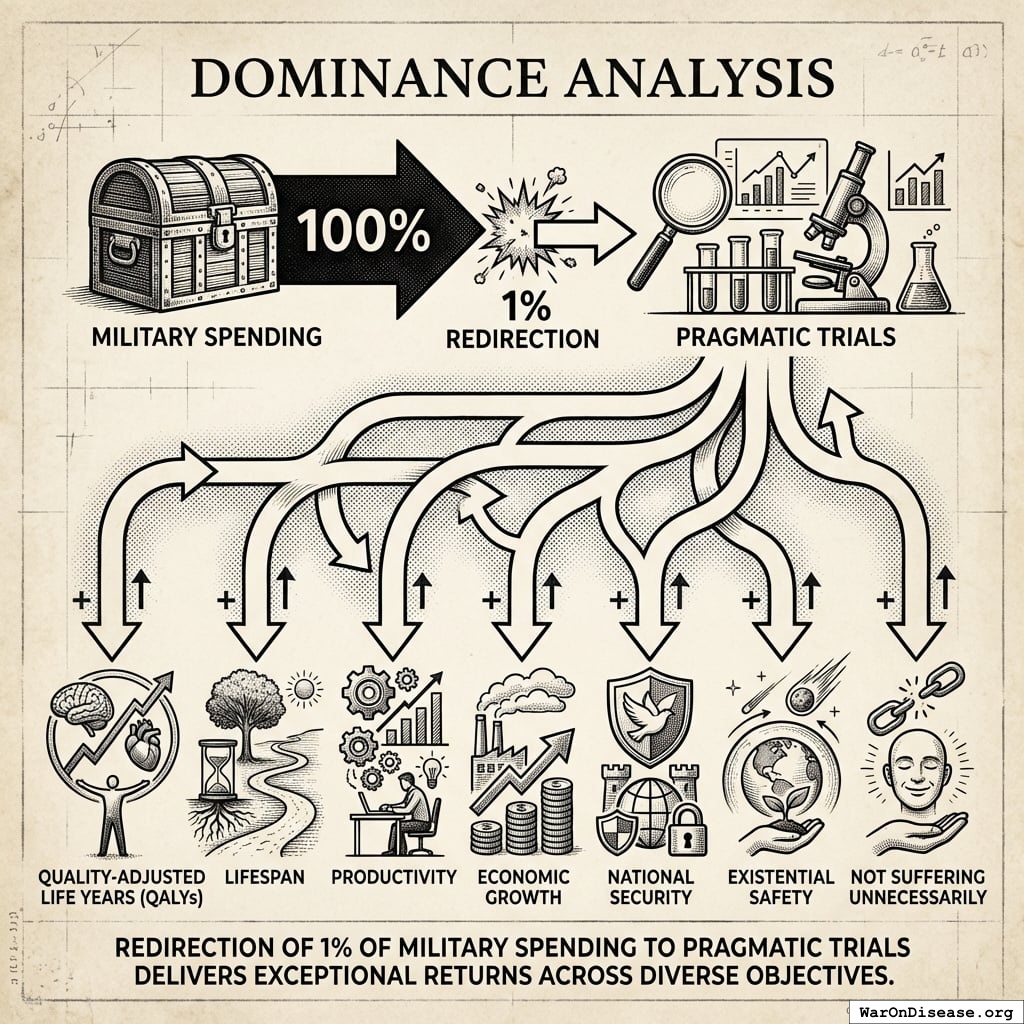
Dominance Analysis
For objectives including:
- Quality-adjusted life years (QALYs)
- Lifespan
- Productivity
- Economic growth
- National security
- Existential safety
- Not suffering unnecessarily
Redirection of 1% of military spending to pragmatic trials delivers exceptional returns.
Quantitative Comparison
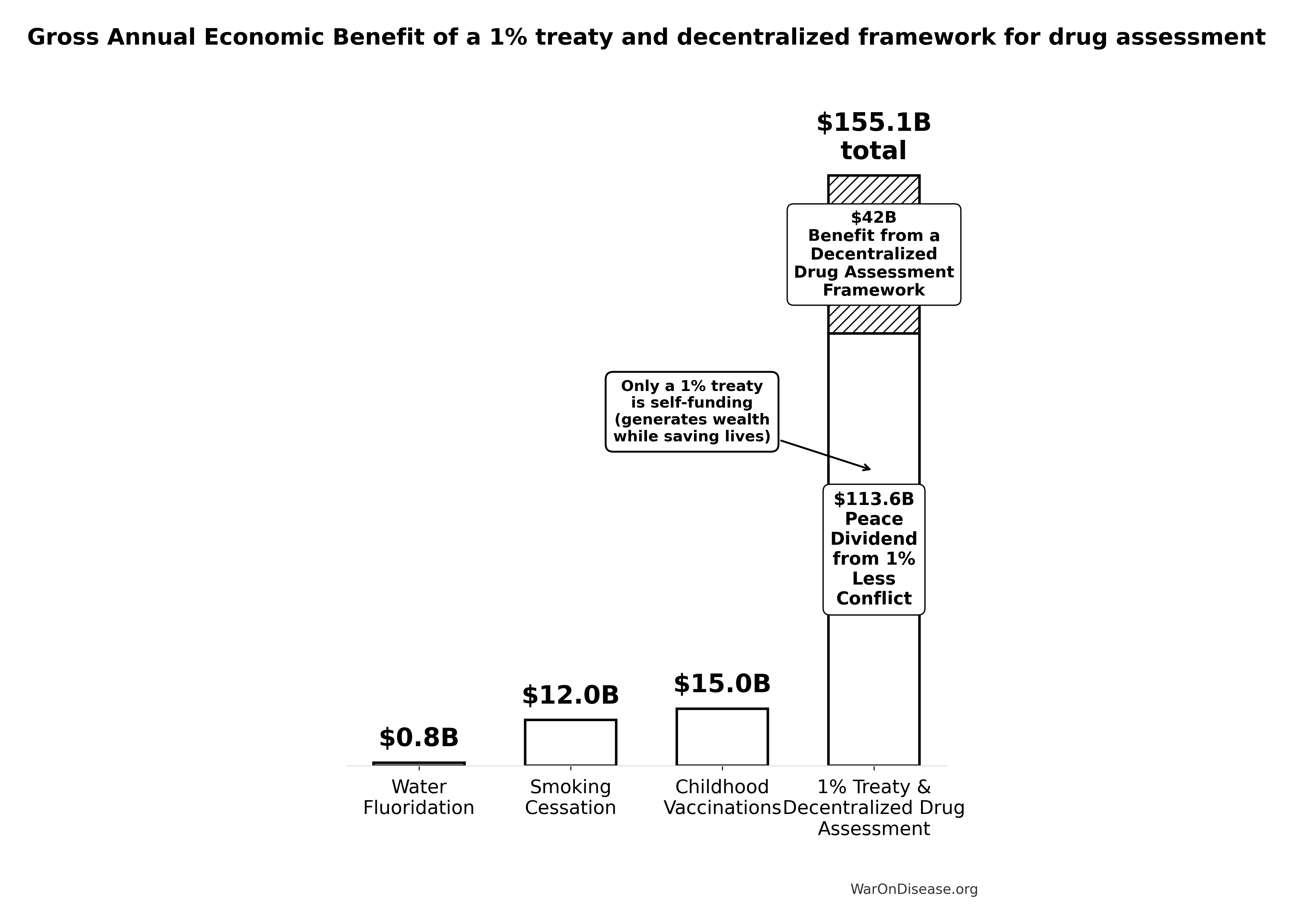
With $1B allocated toward saving lives, here’s what each option delivers:
Conservative benefits ($172B (95% CI: $140B-$213B) annually) exceed childhood vaccinations by 11.5x (95% CI: 9x-16.1x).
\[
\begin{gathered}
k_{treaty:vax} \\
= \frac{Benefit_{peace+RD}}{Benefit_{vax,ann}} \\
= \frac{\$172B}{\$15B} \\
= 11.5
\end{gathered}
\] where: \[
\begin{gathered}
Benefit_{peace+RD} \\
= Benefit_{peace,soc} + Benefit_{RD,ann} \\
= \$114B + \$58.6B \\
= \$172B
\end{gathered}
\] where: \[
\begin{gathered}
Benefit_{peace,soc} \\
= Cost_{war,total} \times Reduce_{treaty} \\
= \$11.4T \times 1\% \\
= \$114B
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{war,total} \\
= Cost_{war,direct} + Cost_{war,indirect} \\
= \$7.66T + \$3.7T \\
= \$11.4T
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{war,direct} \\
= Loss_{life,conflict} + Damage_{infra,total} \\
+ Disruption_{trade} + Spending_{mil} \\
= \$2.45T + \$1.88T + \$616B + \$2.72T \\
= \$7.66T
\end{gathered}
\] where: \[
\begin{gathered}
Loss_{life,conflict} \\
= Cost_{combat,human} + Cost_{state,human} \\
+ Cost_{terror,human} \\
= \$2.34T + \$27B + \$83B \\
= \$2.45T
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{combat,human} \\
= Deaths_{combat} \times VSL \\
= 234{,}000 \times \$10M \\
= \$2.34T
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{state,human} \\
= Deaths_{state} \times VSL \\
= 2{,}700 \times \$10M \\
= \$27B
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{terror,human} \\
= Deaths_{terror} \times VSL \\
= 8{,}300 \times \$10M \\
= \$83B
\end{gathered}
\] where: \[
\begin{gathered}
Damage_{infra,total} \\
= Damage_{comms} + Damage_{edu} + Damage_{energy} \\
+ Damage_{health} + Damage_{transport} + Damage_{water} \\
= \$298B + \$234B + \$422B + \$166B + \$487B + \$268B \\
= \$1.88T
\end{gathered}
\] where: \[
\begin{gathered}
Disruption_{trade} \\
= Disruption_{currency} + Disruption_{energy} \\
+ Disruption_{shipping} + Disruption_{supply} \\
= \$57.4B + \$125B + \$247B + \$187B \\
= \$616B
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{war,indirect} \\
= Damage_{env} + Loss_{growth,mil} + Loss_{capital,conflict} \\
+ Cost_{psych} + Cost_{refugee} + Cost_{vet} \\
= \$100B + \$2.72T + \$300B + \$232B + \$150B + \$200B \\
= \$3.7T
\end{gathered}
\] where: \[
\begin{gathered}
Benefit_{RD,ann} \\
= Spending_{trials} \times Reduce_{pct} \\
= \$60B \times 97.7\% \\
= \$58.6B
\end{gathered}
\] where: \[
\begin{gathered}
Reduce_{pct} \\
= 1 - \frac{Cost_{pragmatic,pt}}{Cost_{P3,pt}} \\
= 1 - \frac{\$929}{\$41K} \\
= 97.7\%
\end{gathered}
\]
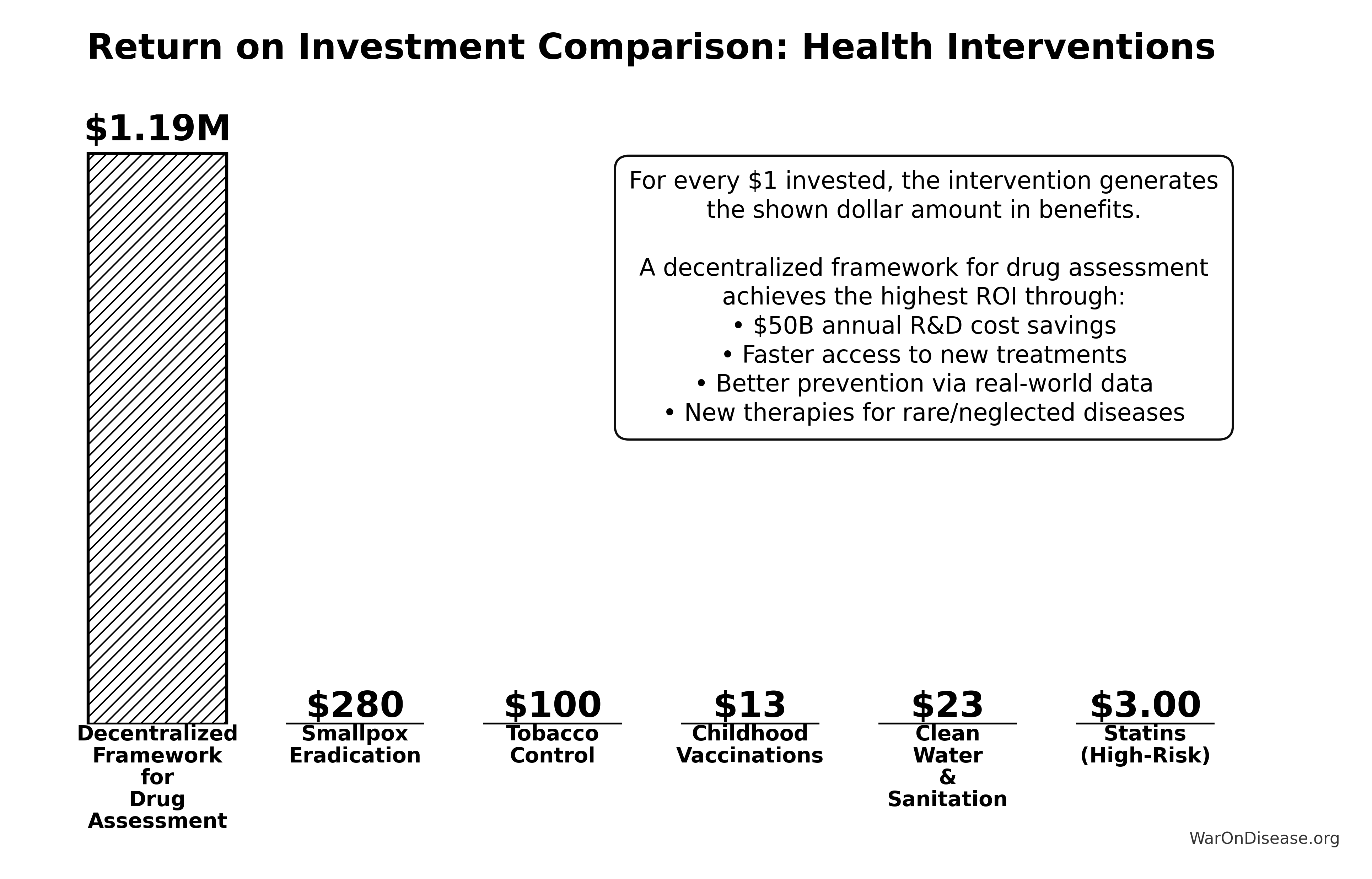
GiveWell Top Charities (individual benchmarks):
Why the 50.3kx (95% CI: 23.7kx-111.7kx) better cost-effectiveness vs. bed nets is plausible:
Bed nets are consumable interventions requiring ongoing replacement every 3-5 years. To save 1,000 lives over 20 years requires purchasing and distributing thousands of bed nets repeatedly. Total cost scales linearly with lives saved.
The 1% Treaty is a one-time implementation cost ($1B) that unlocks a permanent infrastructure shift. Once the treaty passes, it redirects $27.2B/year in perpetuity, funding millions of trial participants annually. The implementation cost is paid once; the benefits compound indefinitely.
Asset class comparison: Bed nets are depreciating assets (consumed, worn out, require replacement). Medical treatments are appreciating assets. Once discovered, they compound in value forever; penicillin discovered in 1928 still saves lives today. Military spending creates depreciating assets (weapons become obsolete, require replacement). This reallocation shifts capital from depreciating to appreciating asset classes, explaining why ROI can be 50.3kx (95% CI: 23.7kx-111.7kx) better than excellent consumable interventions like bed nets.
\[
\begin{gathered}
k_{treaty:nets} \\
= \frac{Cost_{nets}}{Cost_{treaty,DALY}} \\
= \frac{\$89}{\$0.00177} \\
= 50{,}300
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{treaty,DALY} \\
= \frac{Cost_{campaign}}{DALYs_{max}} \\
= \frac{\$1B}{565B} \\
= \$0.00177
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{campaign} \\
= Budget_{viral,base} + Budget_{lobby,treaty} \\
+ Budget_{reserve} \\
= \$250M + \$650M + \$100M \\
= \$1B
\end{gathered}
\] where: \[
\begin{gathered}
DALYs_{max} \\
= DALYs_{global,ann} \times Pct_{avoid,DALY} \times T_{accel,max} \\
= 2.88B \times 92.6\% \times 212 \\
= 565B
\end{gathered}
\] where: \[
T_{accel,max} = T_{accel} + T_{lag} = 204 + 8.2 = 212
\] where: \[
\begin{gathered}
T_{accel} \\
= T_{first,SQ} \times \left(1 - \frac{1}{k_{capacity}}\right) \\
= 222 \times \left(1 - \frac{1}{12.3}\right) \\
= 204
\end{gathered}
\] where: \[
\begin{gathered}
T_{first,SQ} \\
= T_{queue,SQ} \times 0.5 \\
= 443 \times 0.5 \\
= 222
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\]
Methodology
This analysis uses three standard health economics tools:
- Net Present Value (NPV): Future money is worth less than current money because humans are impatient
- Quality-Adjusted Life Years (QALYs): Measuring healthy life, not just survival - a year lived in full health scores 1.0, while years with illness or disability score proportionally lower
- Return on Investment (ROI): Economic value generated per dollar invested
The methodology follows standard health economics practices. All parameters, sources, and uncertainty ranges are documented in Parameters and Calculations.
Cost-Benefit Framework
Cost Components
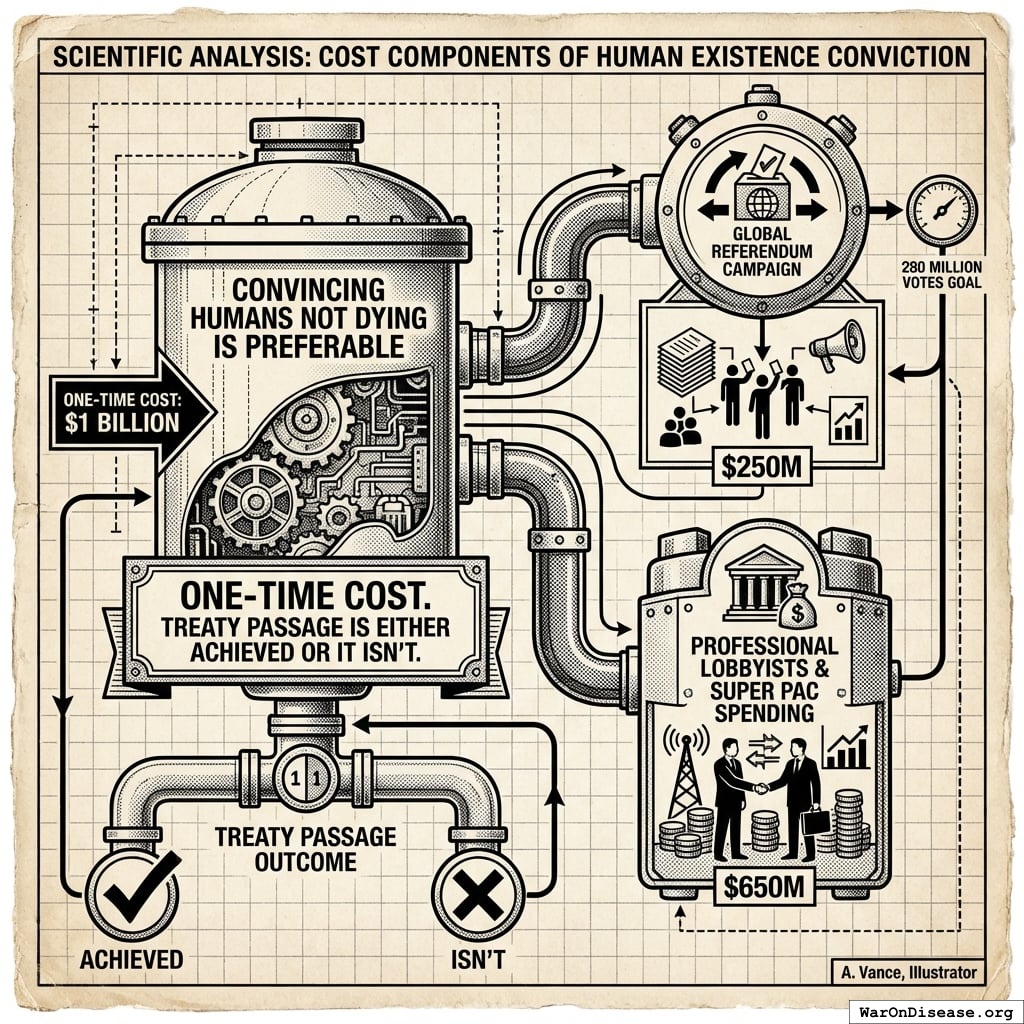
One spends $1B convincing humans that not dying is preferable to dying. This covers:
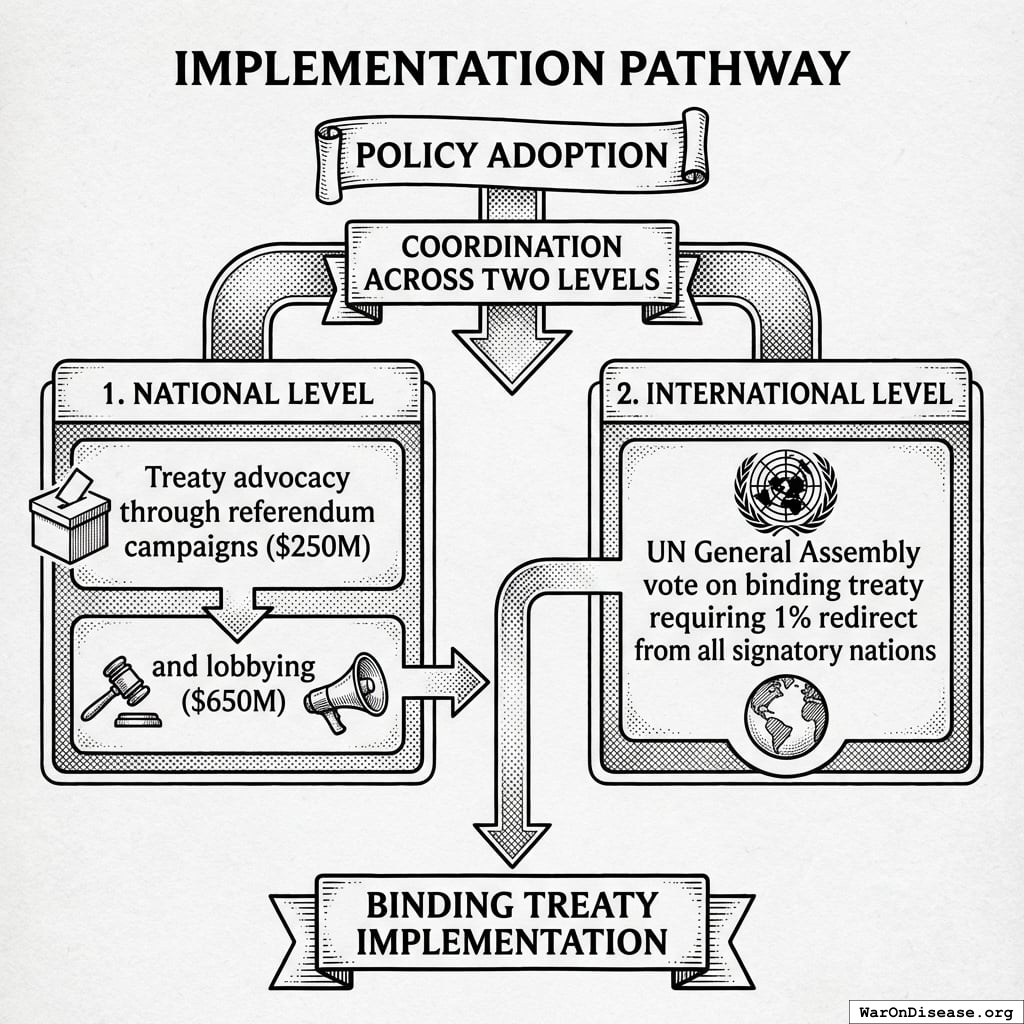
- Global referendum campaign to get 280 million of people votes ($250M)
- Professional lobbyists and Super PAC spending ($650M)
This is a one-time cost. Treaty passage is either achieved or it isn’t.
Benefit Components
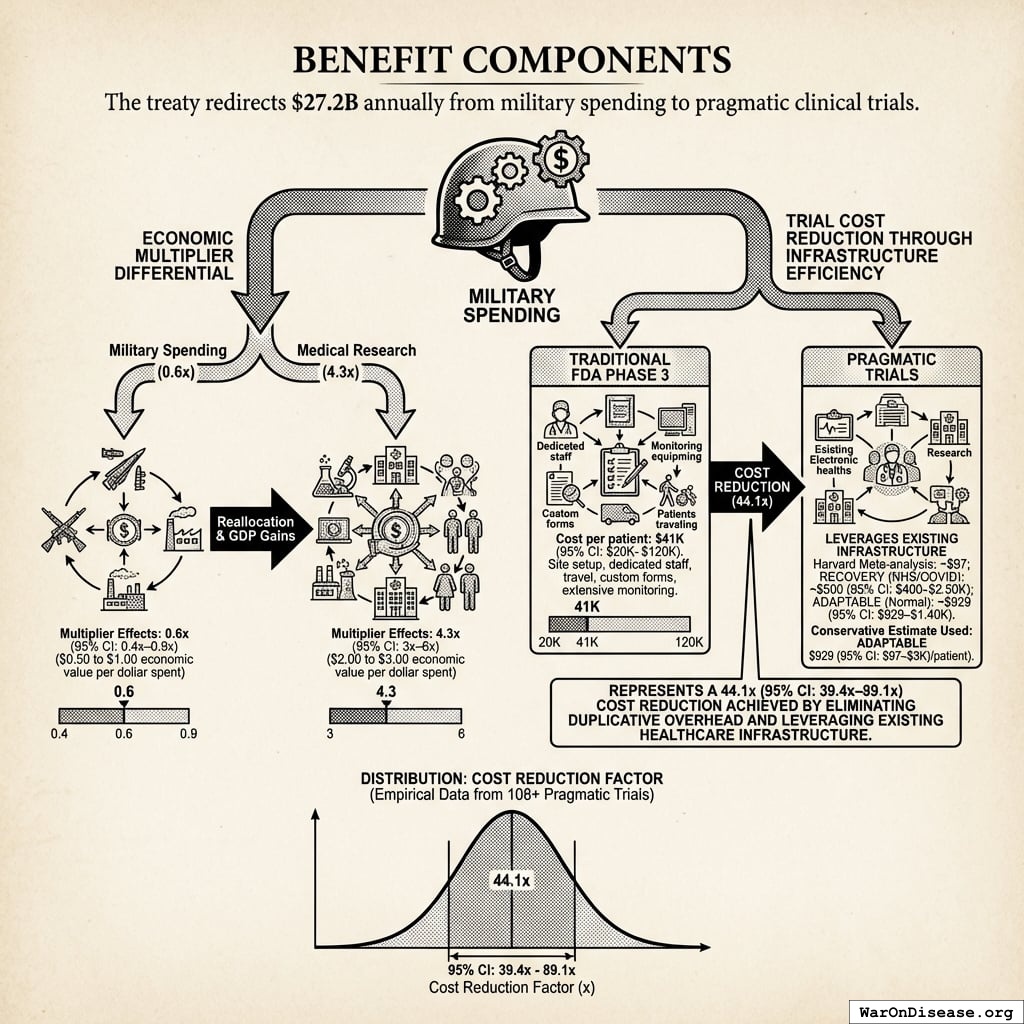
The treaty redirects $27.2B annually from military spending to pragmatic clinical trials.
This generates benefits through two mechanisms:
1. Economic multiplier differential
Military spending generates economic multiplier effects of 0.6x (95% CI: 0.4x-0.9x)26 (50 cents to $1 of economic value per dollar spent). Medical research generates multiplier effects of 4.3x (95% CI: 3x-6x)24 ($2-3 of economic value per dollar spent). Reallocating funds from low-multiplier to high-multiplier activities produces measurable GDP gains.
2. Trial cost reduction through infrastructure efficiency
Traditional FDA Phase 3 trials cost $41K (95% CI: $20K-$120K)101 per patient due to site setup costs, dedicated research staff, patient travel reimbursement, custom case report forms, and extensive monitoring requirements. Pragmatic trials leverage existing infrastructure: the Harvard meta-analysis of 108 embedded pragmatic trials found median costs of $97/patient132, RECOVERY achieved $500 (95% CI: $400-$2.50K)/patient (NHS/COVID conditions), and ADAPTABLE achieved $929 (95% CI: $929-$1.40K)/patient under normal conditions. Our system projections use the conservative ADAPTABLE estimate ($929 (95% CI: $97-$3K)/patient).
This represents a 44.1x (95% CI: 39.4x-89.1x) cost reduction achieved by eliminating duplicative overhead and leveraging existing healthcare infrastructure.
The distribution below shows the uncertainty range for the cost reduction factor based on empirical data from 108+ pragmatic trials:
Simulation Results Summary: RECOVERY Trial Cost Reduction Factor
| Baseline (deterministic) |
82x |
| Mean (expected value) |
71.2x |
| Median (50th percentile) |
72.4x |
| Standard Deviation |
15.3x |
| 90% Range (5th-95th percentile) |
[50x, 94.1x] |
The histogram shows the distribution of RECOVERY Trial Cost Reduction Factor across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
ROI Calculation
In human language: “How much value is generated per dollar spent?”
Conservative scenario (only counting R&D efficiency, ignoring everything else):
Spending $1 returns 637:1 (95% CI: 569:1-790:1). This beats most legal activities.
Complete scenario (PRIMARY estimate including all core benefits):
A $1 billion campaign investment could plausibly generate: (1) a 212 years (95% CI: 135 years-355 years) average timeline shift (the average disease treatment becomes available 212 years (95% CI: 135 years-355 years) earlier), plus (2) $172B (95% CI: $140B-$213B)/year in recurring economic benefits (peace dividend + R&D savings).
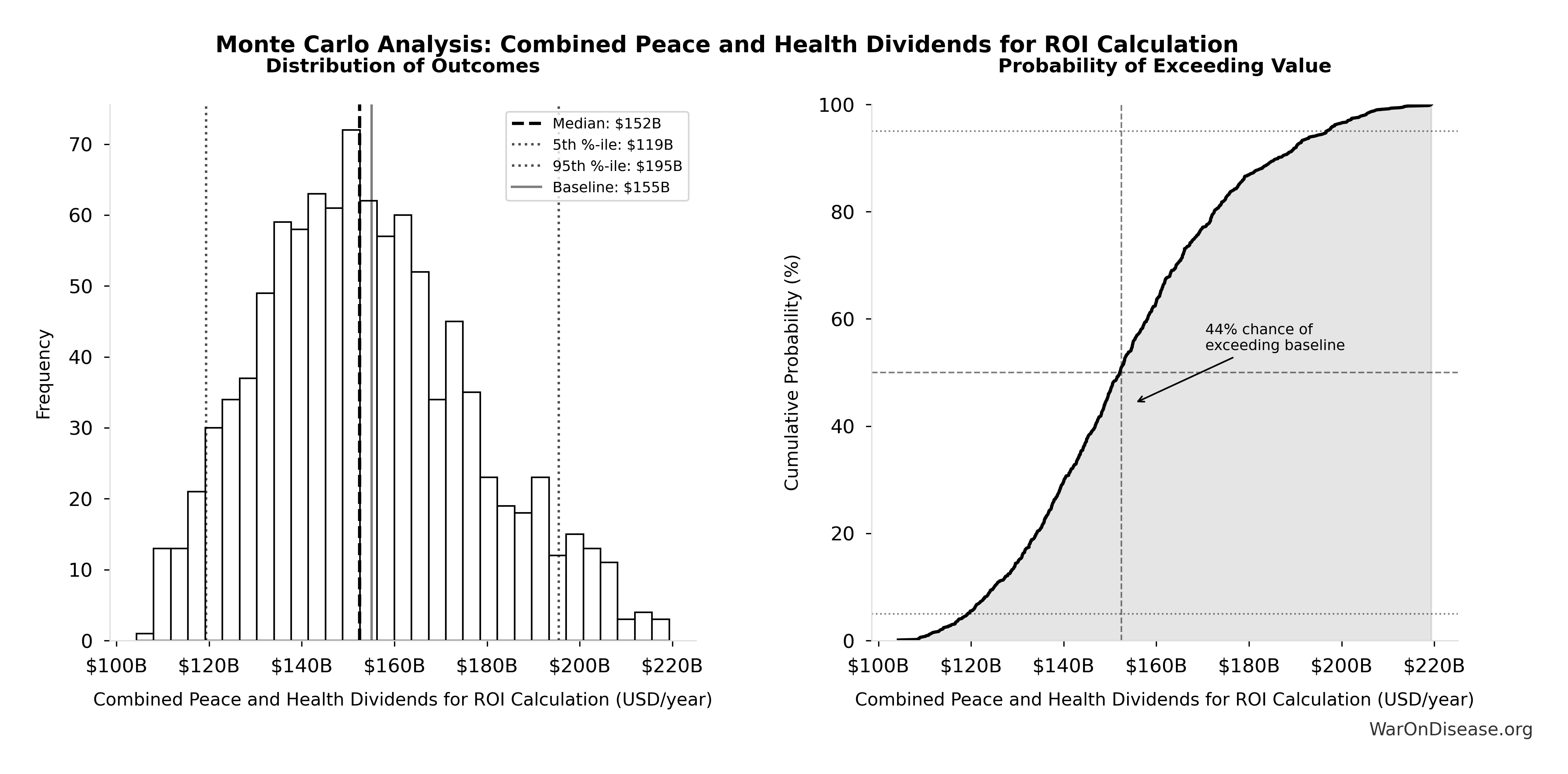
Combined Annual Benefits Uncertainty
The recurring annual benefits combine two streams: peace dividend ($114B (95% CI: $90.1B-$141B)/year) and R&D savings ($58.6B (95% CI: $49.2B-$73.1B)/year).
The tornado diagram shows that peace dividend magnitude and R&D savings dominate the uncertainty in combined annual benefits.
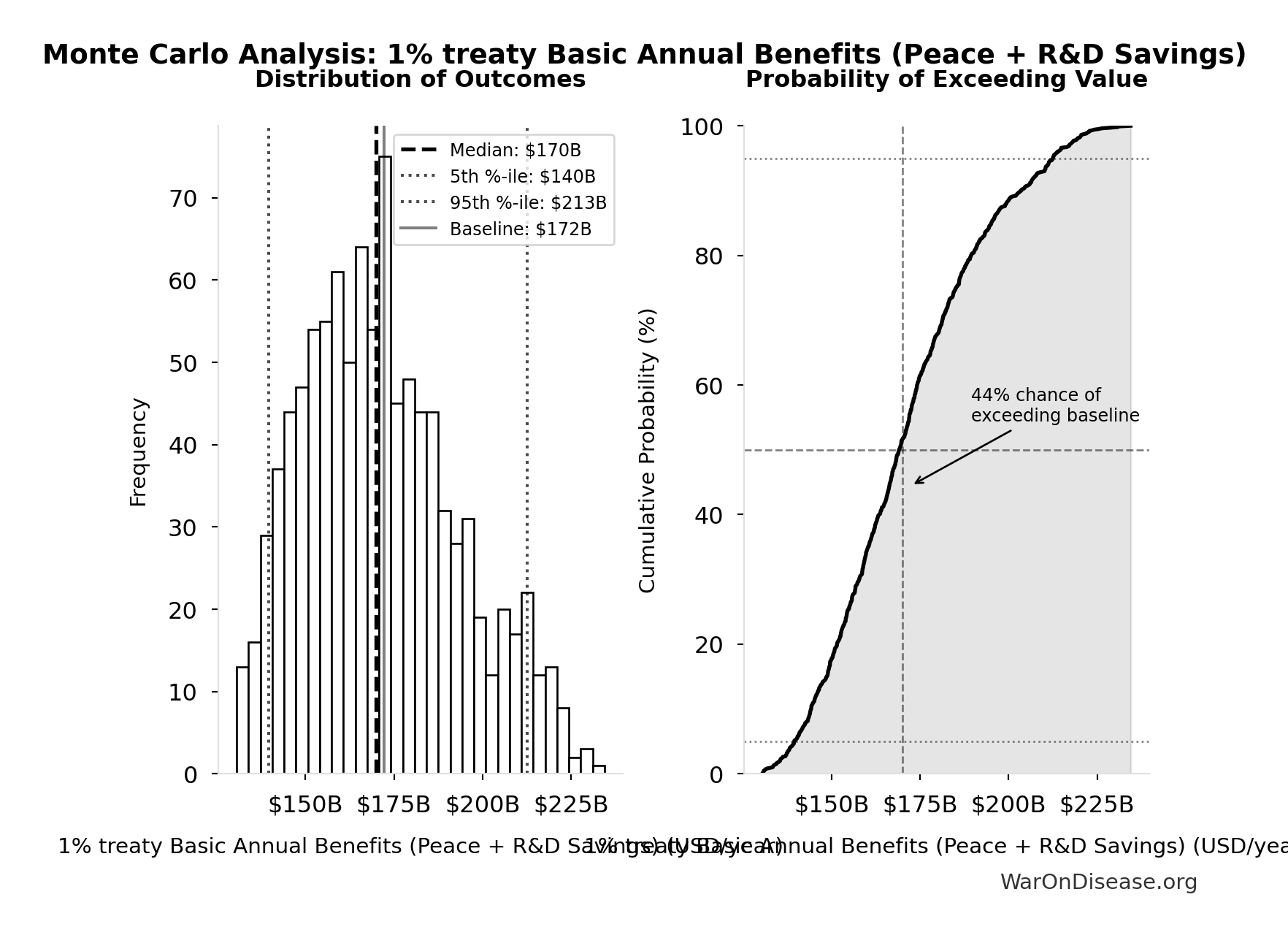
Simulation Results Summary: 1% treaty Basic Annual Benefits (Peace + R&D Savings)
| Baseline (deterministic) |
$172B |
| Mean (expected value) |
$172B |
| Median (50th percentile) |
$170B |
| Standard Deviation |
$22.2B |
| 90% Range (5th-95th percentile) |
[$140B, $213B] |
The histogram shows the distribution of 1% treaty Basic Annual Benefits (Peace + R&D Savings) across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Monte Carlo analysis confirms the intervention generates tens of billions in recurring annual value across all plausible scenarios.
Cost-Effectiveness Analysis
Health economists measure cost-effectiveness as cost per DALY (Disability-Adjusted Life Year): how much does it cost to avert one year of disease burden?
WHO says interventions under $50K130 per DALY are “cost-effective.” Most successful health programs cost $3,000-10,000130 per DALY.
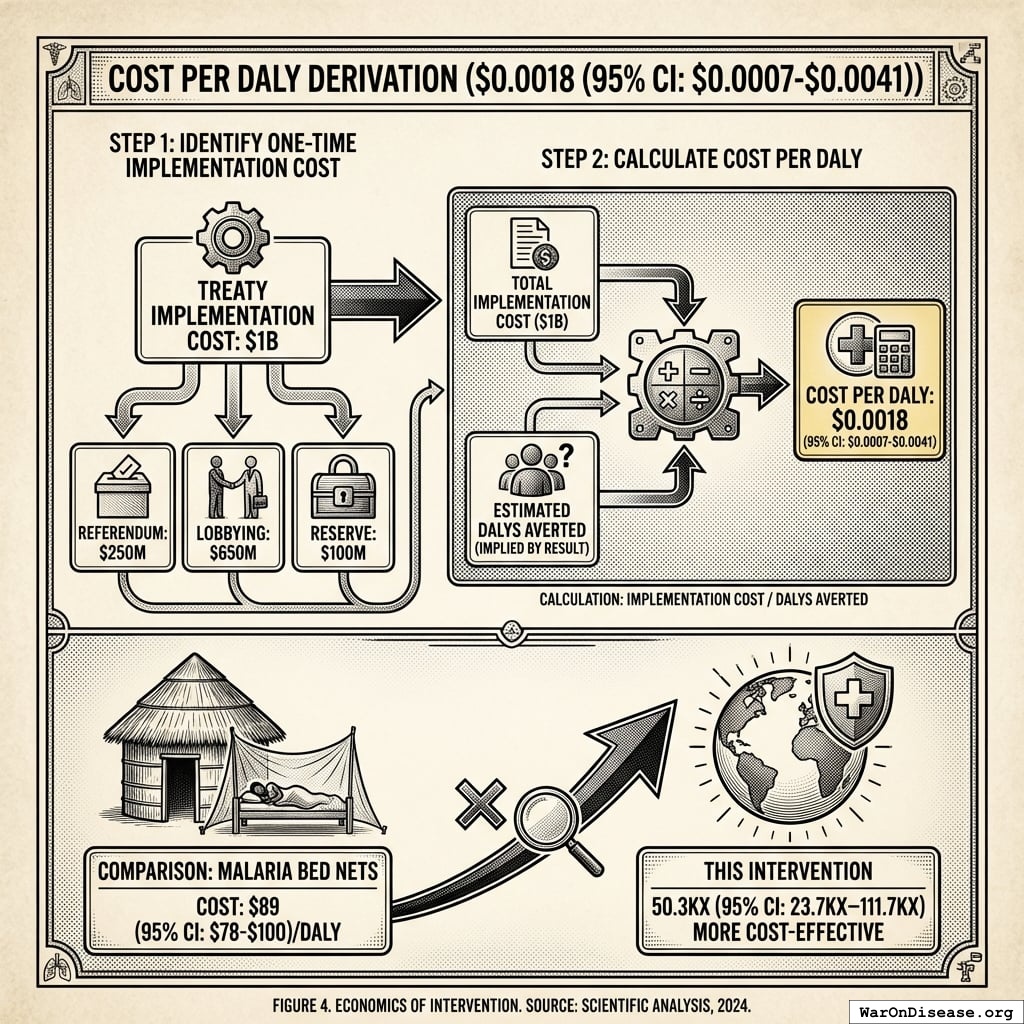
This system’s upfront cost: $0.0018 (95% CI: $0.0007-$0.0041) per DALY
But here’s the key: this intervention is cost-saving. The upfront implementation cost of $0.0018 (95% CI: $0.0007-$0.0041)/DALY unlocks $172B (95% CI: $140B-$213B)/year in recurring economic benefits.
Technical note: This uses “net present value,” which is economist code for “future money is worth less than current money” (3% discount rate). For detailed analysis: full NPV methodology here.
Pragmatic Trials vs. NIH Standard Research
NIH Standard Research (Current Status Quo):
Efficiency gap: 12.5kx (95% CI: 2.3kx-51.5kx).
\[
\begin{gathered}
Cost_{pragmatic,QALY} \\
= \frac{Cost_{RECOVERY}}{QALY_{RECOVERY}} \\
= \frac{\$20M}{5M} \\
= \$4
\end{gathered}
\] where: \[
\begin{gathered}
QALY_{RECOVERY} \\
= Lives_{RECOVERY} \times QALY_{COVID} \\
= 1M \times 5 \\
= 5M
\end{gathered}
\]
\[
\begin{gathered}
k_{pragmatic:NIH} \\
= \frac{Cost_{NIH,QALY}}{Cost_{pragmatic,QALY}} \\
= \frac{\$50K}{\$4} \\
= 12{,}500
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{pragmatic,QALY} \\
= \frac{Cost_{RECOVERY}}{QALY_{RECOVERY}} \\
= \frac{\$20M}{5M} \\
= \$4
\end{gathered}
\] where: \[
\begin{gathered}
QALY_{RECOVERY} \\
= Lives_{RECOVERY} \times QALY_{COVID} \\
= 1M \times 5 \\
= 5M
\end{gathered}
\]
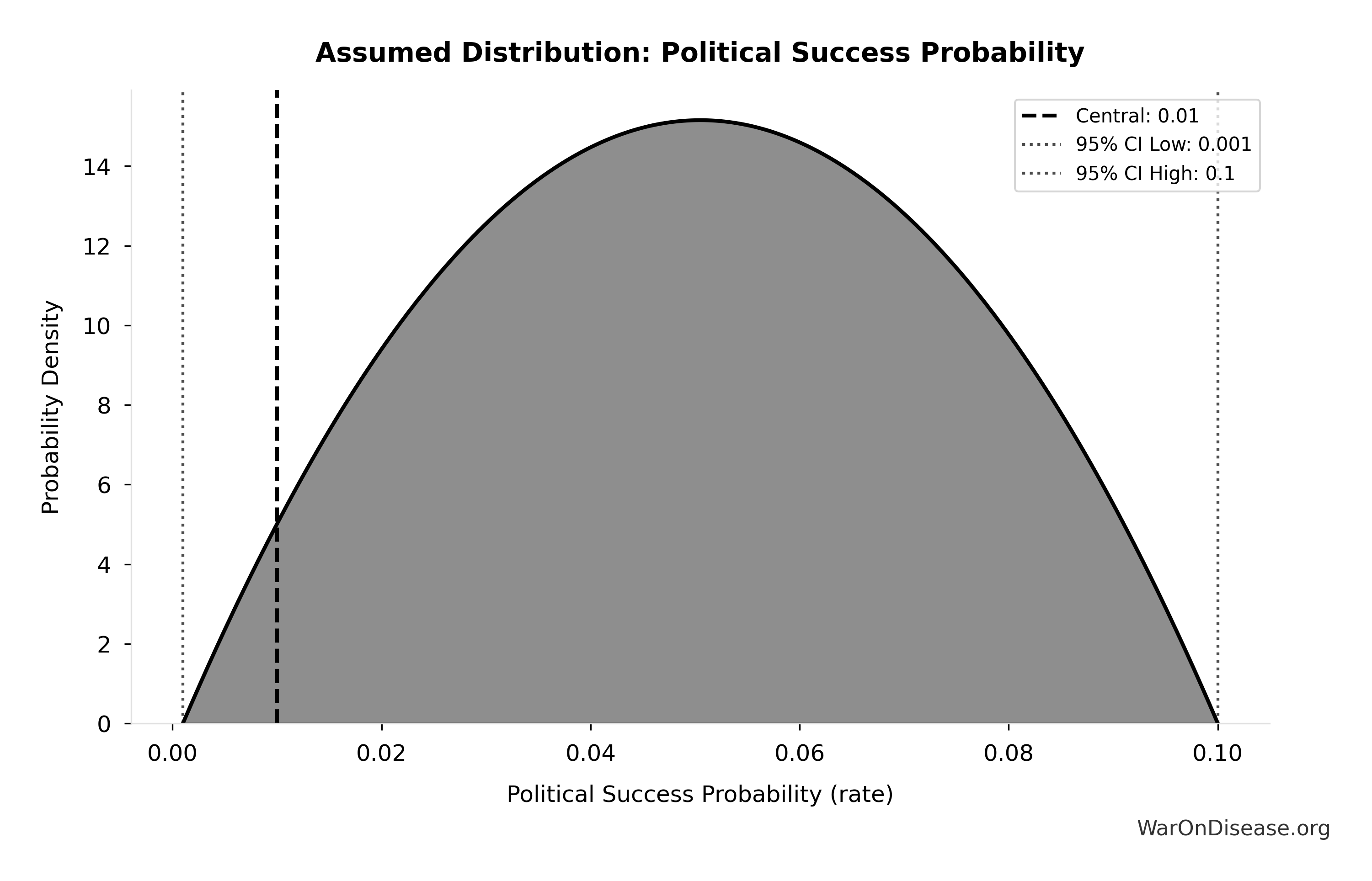
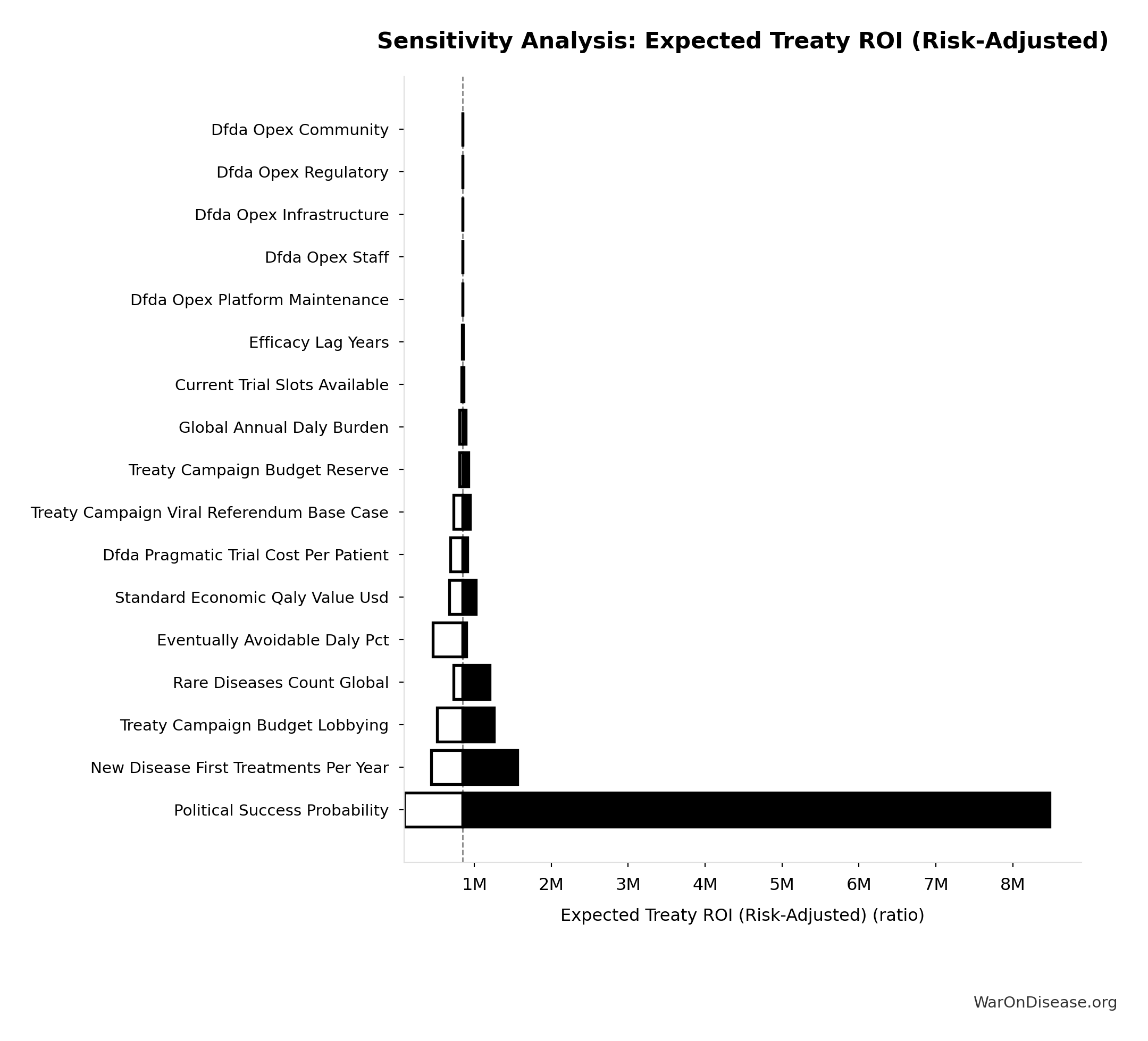
Expected Value Under Political Uncertainty
Conditional on success: $0.0018 (95% CI: $0.0007-$0.0041) per DALY
Risk-adjusted expected value: $0.177 (95% CI: $0.029-$3.20) per DALY
Uncertainty in Risk-Adjusted Cost-Effectiveness
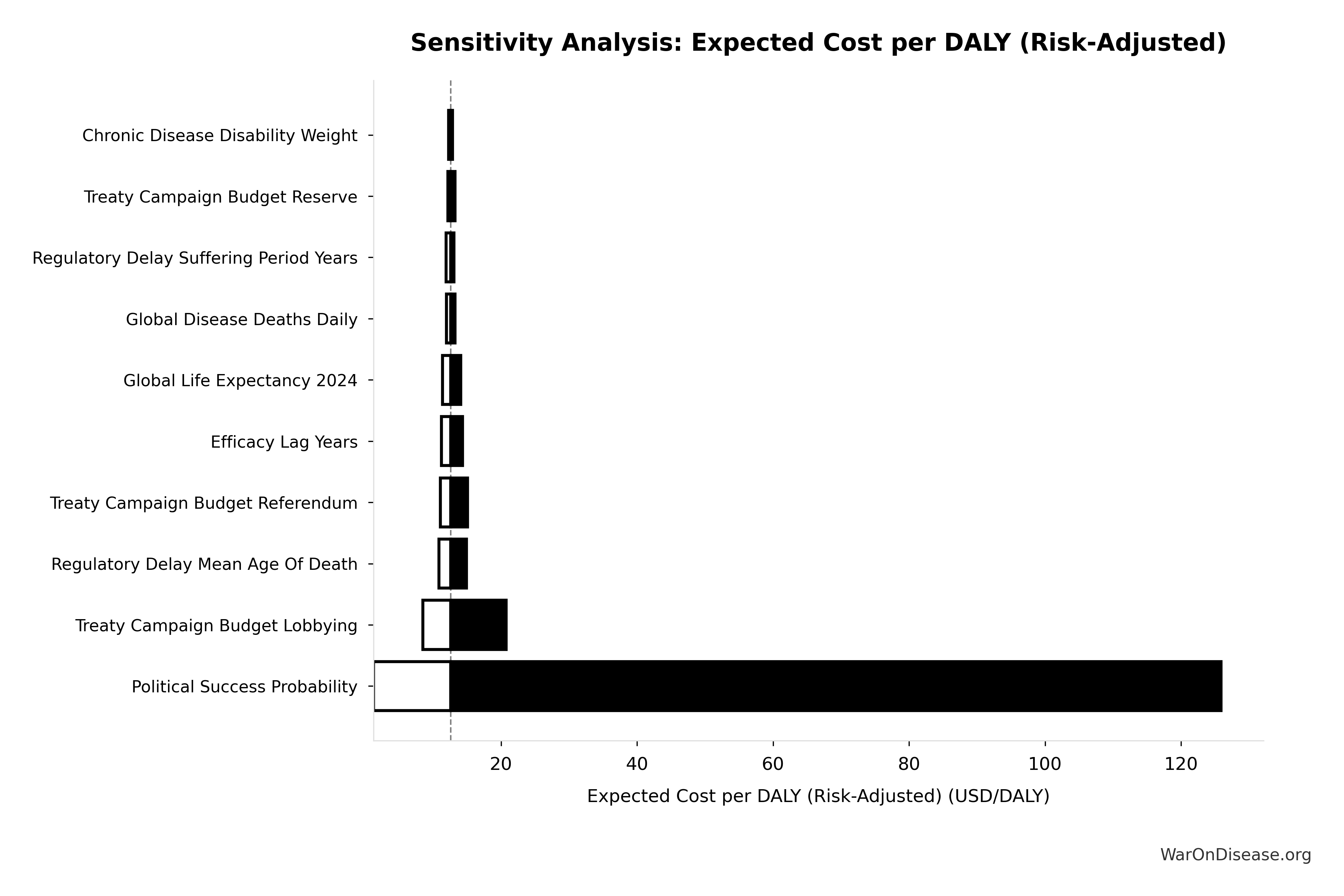
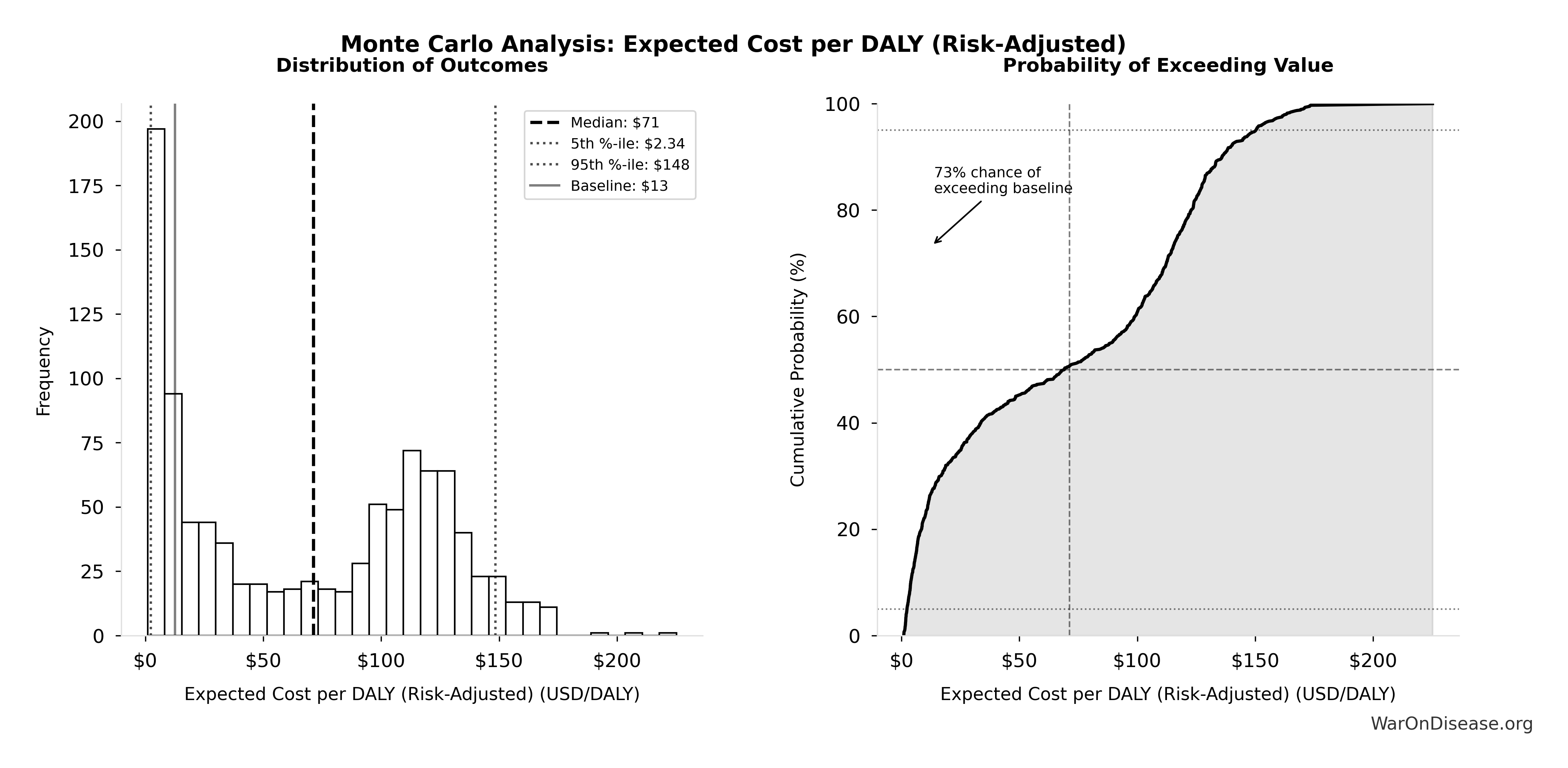
The tornado diagram shows that political success probability dominates uncertainty in risk-adjusted cost-effectiveness. Even at conservative political success estimates, expected cost per DALY remains highly competitive with top global health interventions.
Simulation Results Summary: Expected Cost per DALY (Risk-Adjusted)
| Baseline (deterministic) |
$0.177 |
| Mean (expected value) |
$1.06 |
| Median (50th percentile) |
$0.779 |
| Standard Deviation |
$1.12 |
| 90% Range (5th-95th percentile) |
[$0.029, $3.20] |
The histogram shows the distribution of Expected Cost per DALY (Risk-Adjusted) across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Monte Carlo simulation confirms that accounting for political risk, the 95% confidence interval maintains dominance over established interventions.
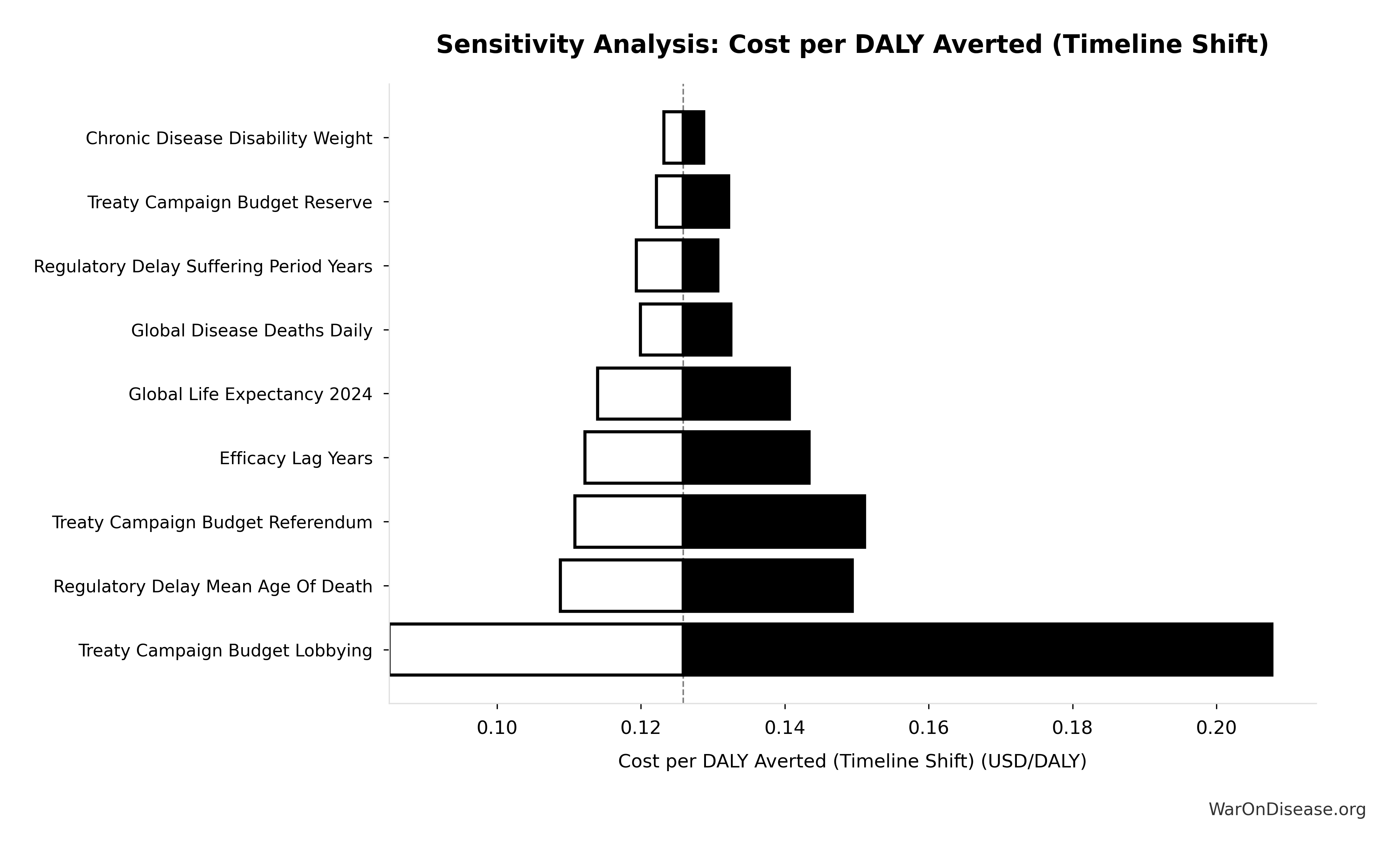
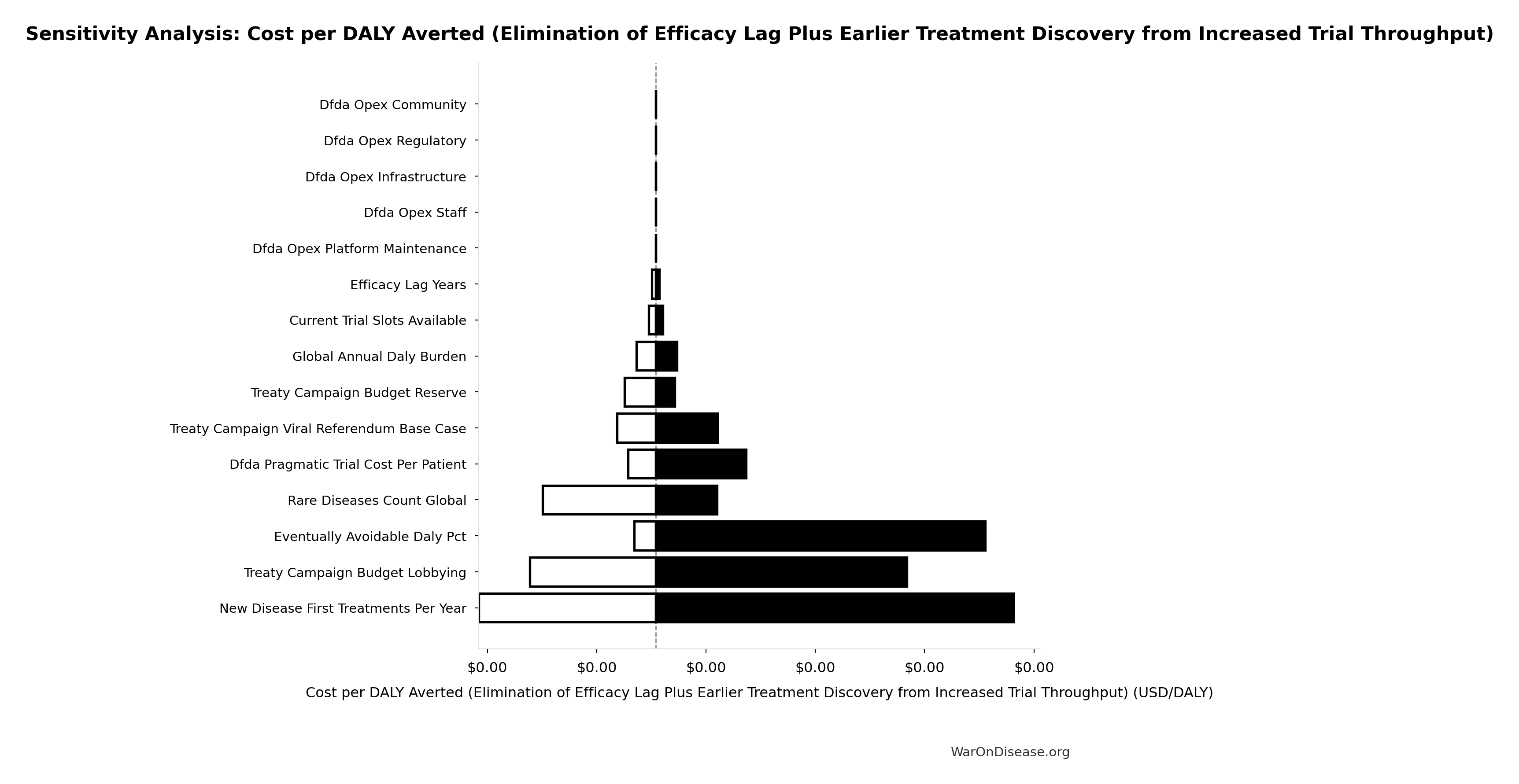
Uncertainty in Cost-Effectiveness (Conditional on Success)
The tornado diagram shows that timeline shift assumptions and discount rate dominate uncertainty in cost-effectiveness. Even under conservative parameter assumptions, the intervention remains highly cost-effective.
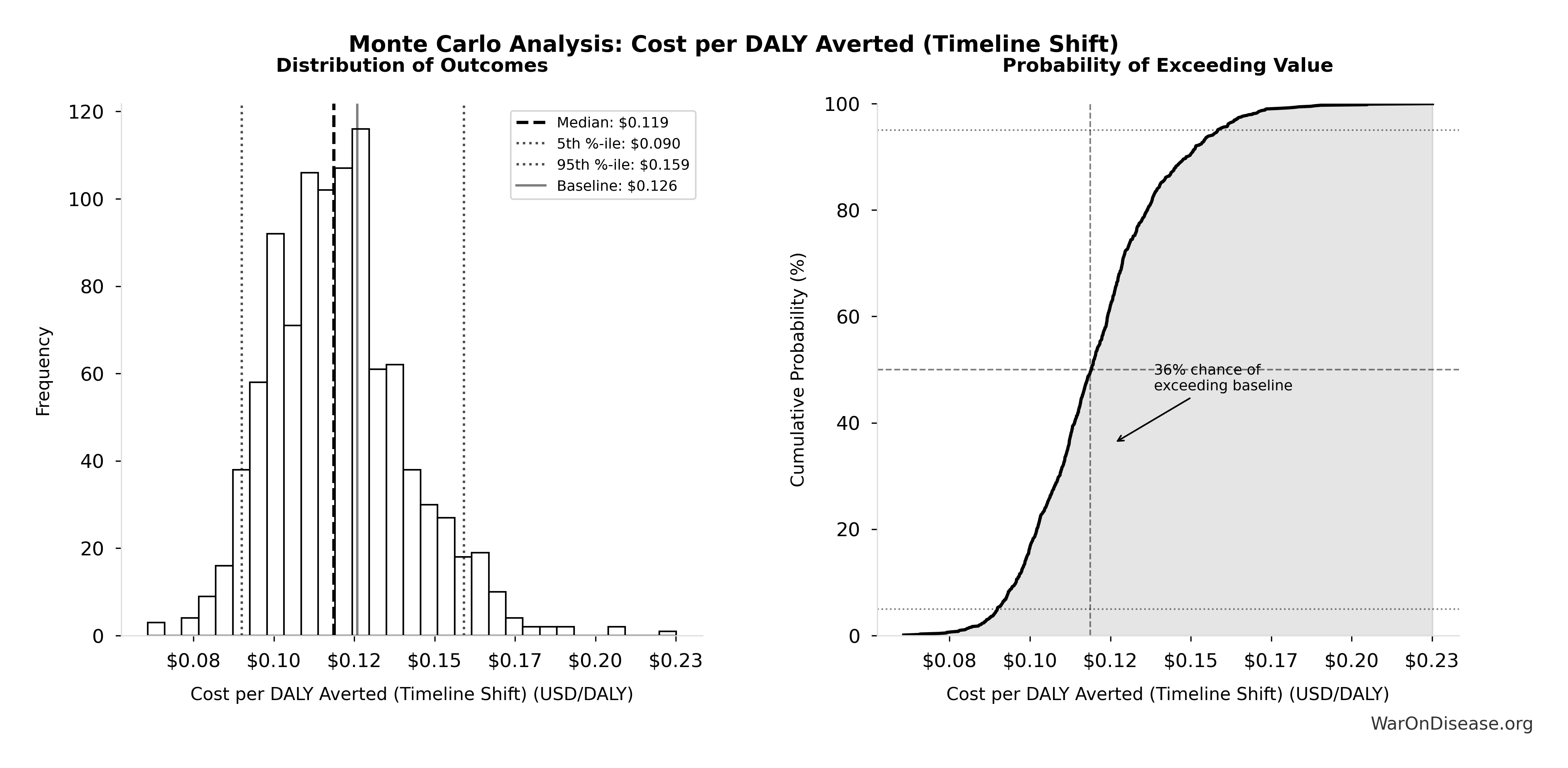
Simulation Results Summary: Cost per DALY Averted (Elimination of Efficacy Lag Plus Earlier Treatment Discovery from Increased Trial Throughput)
| Baseline (deterministic) |
$0.0018 |
| Mean (expected value) |
$0.0019 |
| Median (50th percentile) |
$0.0016 |
| Standard Deviation |
$0.0011 |
| 90% Range (5th-95th percentile) |
[$0.0007, $0.0041] |
The histogram shows the distribution of Cost per DALY Averted (Elimination of Efficacy Lag Plus Earlier Treatment Discovery from Increased Trial Throughput) across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Monte Carlo analysis confirms the 95% confidence interval for cost per DALY remains well below $1/DALY, maintaining dominance.
Accounting for political uncertainty (1% (95% CI: 0.1%-10%)), this remains 503x (95% CI: 29.9x-3.0kx) more cost-effective than bed nets ($89 (95% CI: $78-$100)/DALY) and comparable to deworming, the gold standard.
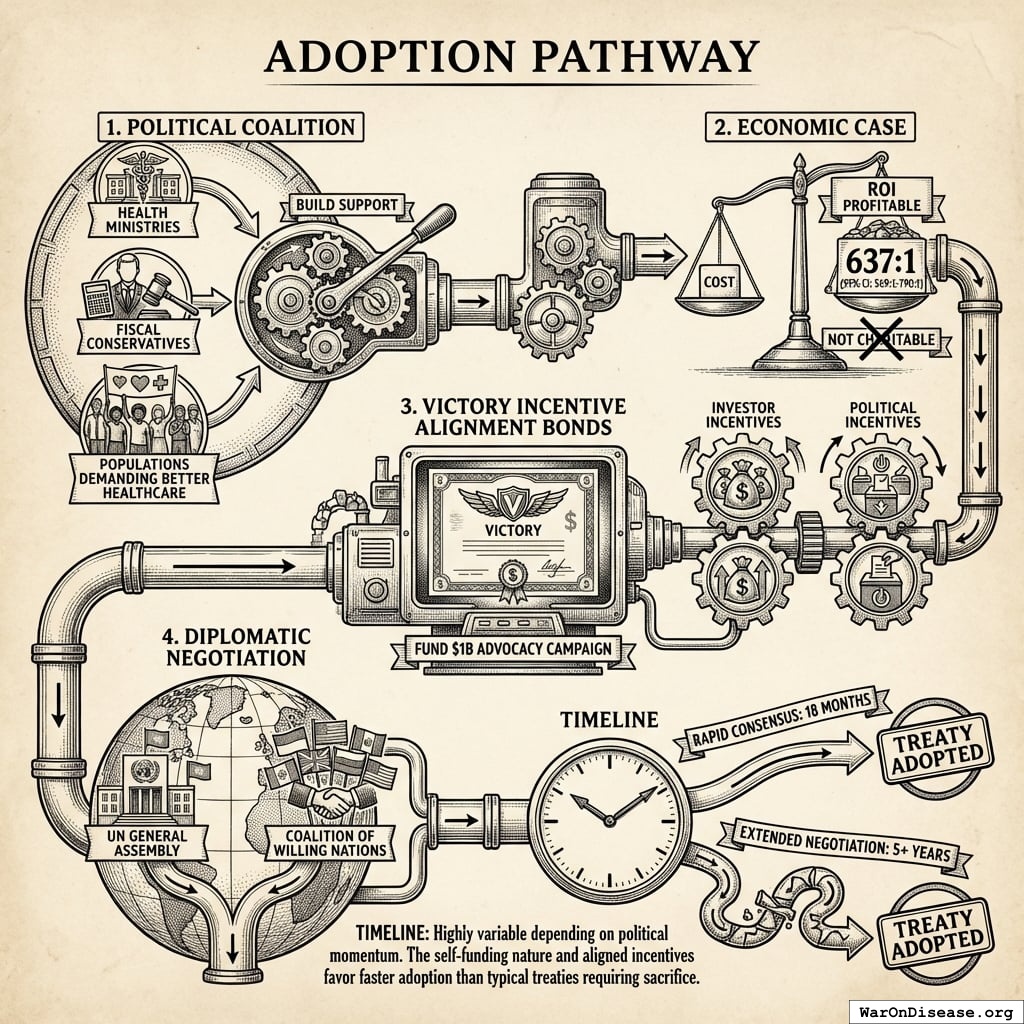
For context: Ottawa Treaty76 (landmine ban) was called a “bold gamble” that succeeded with 122 states signing76 in just 14 months.
Policy Advocacy Leverage vs Direct Funding
A natural question: Why not skip the $1B treaty campaign and simply convince major philanthropists (Gates Foundation, Open Philanthropy) or expand NIH budgets to directly fund $21.8B/year for clinical trials?
Why Billionaires Buy Lottery Tickets Instead of the Casino
The world’s richest people (who will die of cancer, heart disease, or aging just like everyone else) are not exclusively focused on passing this treaty. This is arguably the single most puzzling fact about modern philanthropy.
Four structural barriers explain this coordination failure:
1. The “Bio-Research” Fallacy (buying the wrong asset): Billionaires spend billions on health, but on the wrong part of the supply chain. They build labs (Chan Zuckerberg Biohub, Altos Labs, Broad Institute) and hire Nobel laureates, assuming the bottleneck is scientific discovery. It isn’t. We have thousands of promising compounds on shelves. The real bottleneck is the Clinical Trial Valley of Death: proving drugs work costs $100M-$1B per drug. No amount of “basic science” funding solves the regulatory/cost engine being too slow and expensive. Building a lab wing named after yourself is prestigious; funding a “Treaty Lobbying Organization” is invisible, unsexy, and bureaucratic.
2. The Scale Mismatch: Mark Zuckerberg is worth ~$175B. If he spent every penny, he could fund the US military for approximately 2 months. The only pot of money large enough to fund global disease eradication is the Global Military Budget ($2.72T/year, every year). Billionaires try to pay for the research out of pocket (which runs out) instead of paying for the key (the treaty) that unlocks the government’s vault.
3. The “Politics is Toxic” Problem: To pass a 1% Treaty, you fight the Defense Industrial Complex. Any billionaire saying “take 1% of military budgets” gets immediately attacked as “weak on national security.” Most billionaires are risk-averse regarding public image, preferring “safe” charities (libraries, scholarships, malaria nets) over “radical” geopolitical restructuring.
4. The “Advisor” Agency Problem: Who advises billionaires? Scientists say “give money to my university lab.” Wealth managers say “don’t do anything politically controversial.” Almost no one in a billionaire’s inner circle is a “Grand Strategy” expert who would say: “The most efficient use of your capital is not to hire scientists, but to hire lobbyists to force governments to redirect 1% of military spending into a decentralized clinical trial framework.”
The arbitrage opportunity: Billionaires are buying lottery tickets (individual research projects with 0.01% probability of curing cancer) when they should be buying the casino (changing the rules via treaty). A billionaire spends $1B on a cancer center with ~0.01% probability of success. The same $1B spent on treaty campaign has ~1% (95% CI: 0.1%-10%) probability of unlocking $27.2B/year forever. The “lobbying” bet is mathematically thousands of times better than the “science” bet, but feels “weird” because it’s political, not medical.
Numerical Comparison: Treaty vs Direct Funding
The answer reveals the treaty campaign’s massive leverage advantage:
Direct Funding Scenario
If philanthropists/NIH directly funded $21.8B/year for 36 years (95% CI: 11.6 years-77.2 years) (therapeutic space exploration period):
\[
NPV_{direct} = Funding_{ann} \times \frac{1 - (1+r)^{-T}}{r}
\]
\[
\begin{gathered}
Cost_{direct,DALY} \\
= \frac{NPV_{direct}}{DALYs_{max}} \\
= \frac{\$475B}{565B} \\
= \$0.841
\end{gathered}
\] where: \[
NPV_{direct} = Funding_{ann} \times \frac{1 - (1+r)^{-T}}{r}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,dFDA} \\
= \frac{T_{queue,SQ}}{k_{capacity}} \\
= \frac{443}{12.3} \\
= 36
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
DALYs_{max} \\
= DALYs_{global,ann} \times Pct_{avoid,DALY} \times T_{accel,max} \\
= 2.88B \times 92.6\% \times 212 \\
= 565B
\end{gathered}
\] where: \[
T_{accel,max} = T_{accel} + T_{lag} = 204 + 8.2 = 212
\] where: \[
\begin{gathered}
T_{accel} \\
= T_{first,SQ} \times \left(1 - \frac{1}{k_{capacity}}\right) \\
= 222 \times \left(1 - \frac{1}{12.3}\right) \\
= 204
\end{gathered}
\] where: \[
\begin{gathered}
T_{first,SQ} \\
= T_{queue,SQ} \times 0.5 \\
= 443 \times 0.5 \\
= 222
\end{gathered}
\]
Direct Funding Still Excellent
Even without treaty leverage, direct funding achieves $0.841 (95% CI: $0.242-$1.75)/DALY - competitive with GiveWell’s top interventions (bed nets at $89 (95% CI: $78-$100)/DALY). This validates the pragmatic trial model independent of political feasibility.
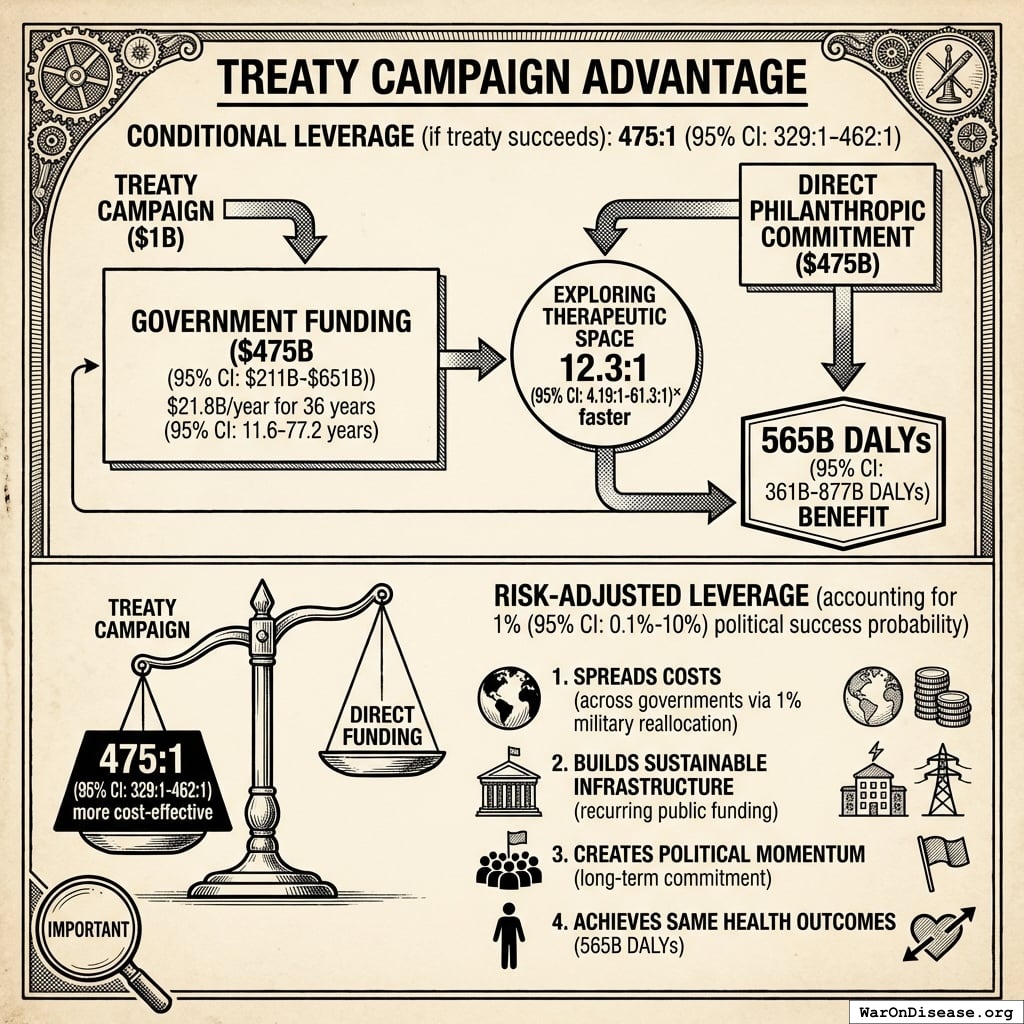
Treaty Campaign Advantage
Conditional leverage (if treaty succeeds): 475x (95% CI: 329x-462x)
The $1B treaty campaign unlocks the same $475B (95% CI: $211B-$651B) in government funding ($21.8B/year for 36 years (95% CI: 11.6 years-77.2 years)) that would otherwise require direct philanthropic commitment. Both approaches achieve the same 565 billion DALYs (95% CI: 361 billion DALYs-877 billion DALYs) benefit by exploring the therapeutic space 12.3x (95% CI: 4.19x-61.3x) faster.
Risk-adjusted leverage (accounting for 1% (95% CI: 0.1%-10%) political success probability):
\[
\begin{gathered}
Leverage_{treaty} \\
= \frac{Cost_{direct,DALY}}{Cost_{treaty,DALY}} \\
= \frac{\$0.841}{\$0.00177} \\
= 475
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{direct,DALY} \\
= \frac{NPV_{direct}}{DALYs_{max}} \\
= \frac{\$475B}{565B} \\
= \$0.841
\end{gathered}
\] where: \[
NPV_{direct} = Funding_{ann} \times \frac{1 - (1+r)^{-T}}{r}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,dFDA} \\
= \frac{T_{queue,SQ}}{k_{capacity}} \\
= \frac{443}{12.3} \\
= 36
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
DALYs_{max} \\
= DALYs_{global,ann} \times Pct_{avoid,DALY} \times T_{accel,max} \\
= 2.88B \times 92.6\% \times 212 \\
= 565B
\end{gathered}
\] where: \[
T_{accel,max} = T_{accel} + T_{lag} = 204 + 8.2 = 212
\] where: \[
\begin{gathered}
T_{accel} \\
= T_{first,SQ} \times \left(1 - \frac{1}{k_{capacity}}\right) \\
= 222 \times \left(1 - \frac{1}{12.3}\right) \\
= 204
\end{gathered}
\] where: \[
\begin{gathered}
T_{first,SQ} \\
= T_{queue,SQ} \times 0.5 \\
= 443 \times 0.5 \\
= 222
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{treaty,DALY} \\
= \frac{Cost_{campaign}}{DALYs_{max}} \\
= \frac{\$1B}{565B} \\
= \$0.00177
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{campaign} \\
= Budget_{viral,base} + Budget_{lobby,treaty} \\
+ Budget_{reserve} \\
= \$250M + \$650M + \$100M \\
= \$1B
\end{gathered}
\]
Even accounting for political risk, the treaty campaign remains 475x (95% CI: 329x-462x) more cost-effective than direct funding. The treaty approach:
- Spreads costs across governments via 1% military reallocation (not reliant on individual philanthropists)
- Builds sustainable infrastructure for recurring public funding (not dependent on continued philanthropic willingness)
- Creates political momentum for long-term commitment beyond philanthropic timelines
- Achieves same health outcomes (565 billion DALYs (95% CI: 361 billion DALYs-877 billion DALYs)) at fraction of the cost
Detailed NPV Formulas
NPV of Costs
\[
\begin{gathered}
Cost_{dFDA,total} \\
= PV_{OPEX} + Cost_{upfront,total} \\
= \$342M + \$270M \\
= \$611M
\end{gathered}
\] where: \[
PV_{OPEX} = OPEX_{ann} \times \frac{1 - (1+r)^{-T}}{r}
\] where: \[
\begin{gathered}
OPEX_{total} \\
= OPEX_{ann} + OPEX_{DIH,ann} \\
= \$18.9M + \$21.1M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{upfront,total} \\
= Cost_{upfront} + Cost_{DIH,init} \\
= \$40M + \$230M \\
= \$270M
\end{gathered}
\]
where \(C_{0}\) is upfront costs (platform development, legal structure, data integration), \(C_{\text{op}}(t)\) is annual operating costs in year \(t\) (maintenance, analysis, administration), \(r\) is the discount rate (3%), and \(T\) is the time horizon (10 years).
NPV of Benefits
Note: The NPV calculation includes only annual recurring R&D savings, not the timeline shift benefits. The full timeline shift (~212 years (95% CI: 135 years-355 years) on average, combining treatment acceleration and efficacy lag elimination) is a separate benefit analyzed below. This section focuses on the efficacy lag component (8.2 years (95% CI: 4.85 years-11.5 years)) for NPV purposes. See Regulatory Mortality Analysis.
Annual benefits \(S(t)\) are calculated as:
\[
S(t) = p(t)\alpha R_{d}
\]
where \(p(t)\) is the adoption rate at year \(t\) (gradual ramp-up over 5 years), \(\alpha\) is the fraction of R&D costs saved (97.7% (95% CI: 97.5%-98.9%) baseline), and \(R_{d}\) is annual global clinical trial spending ($60B (95% CI: $50B-$75B)42).
The NPV of benefits (R&D savings only):
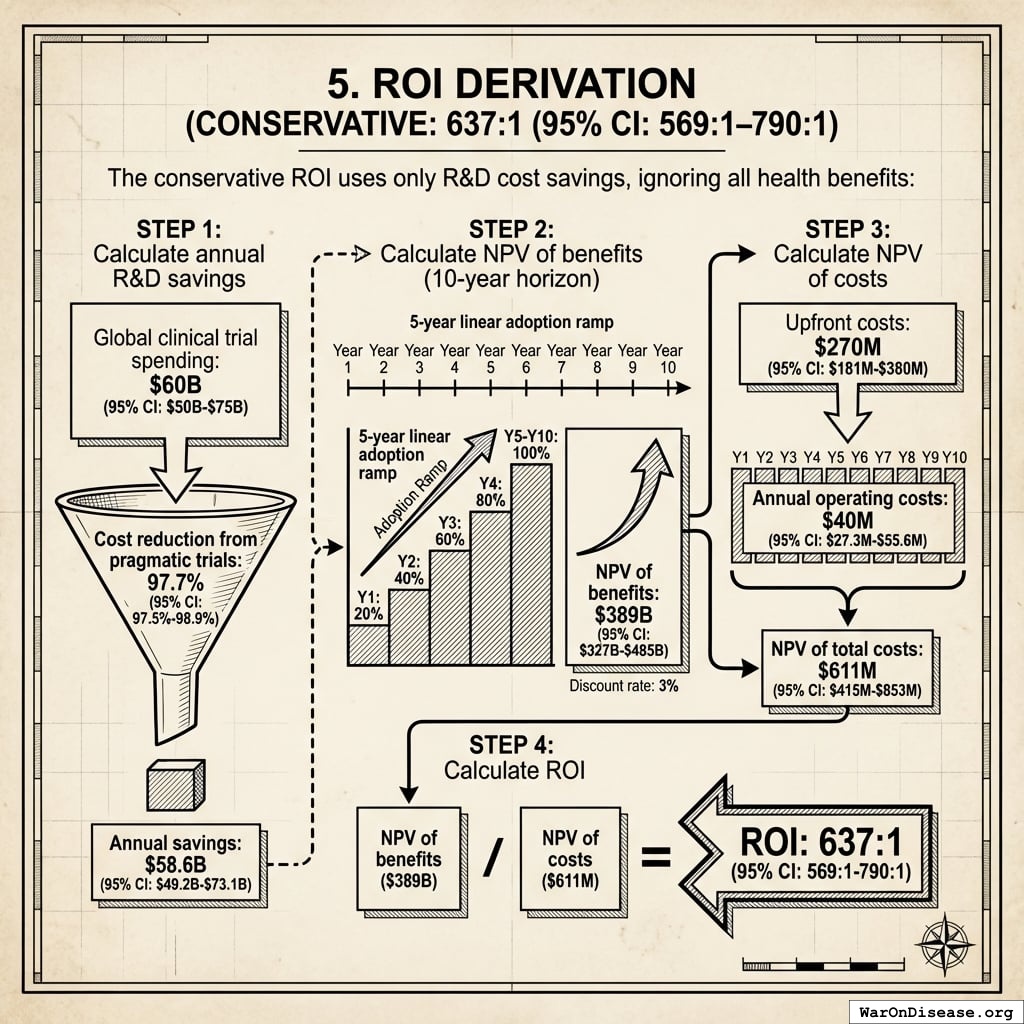
Return on Investment
\[
\begin{gathered}
ROI_{RD} \\
= \frac{NPV_{RD}}{Cost_{dFDA,total}} \\
= \frac{\$389B}{\$611M} \\
= 637
\end{gathered}
\] where: \[
\begin{gathered}
NPV_{RD} \\
= \sum_{t=1}^{10} \frac{Savings_{RD,ann} \times \frac{\min(t,5)}{5}}{(1+r)^t}
\end{gathered}
\] where: \[
\begin{gathered}
Savings_{RD,ann} \\
= Benefit_{RD,ann} - OPEX_{dFDA} \\
= \$58.6B - \$40M \\
= \$58.6B
\end{gathered}
\] where: \[
\begin{gathered}
Benefit_{RD,ann} \\
= Spending_{trials} \times Reduce_{pct} \\
= \$60B \times 97.7\% \\
= \$58.6B
\end{gathered}
\] where: \[
\begin{gathered}
Reduce_{pct} \\
= 1 - \frac{Cost_{pragmatic,pt}}{Cost_{P3,pt}} \\
= 1 - \frac{\$929}{\$41K} \\
= 97.7\%
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{dFDA,total} \\
= PV_{OPEX} + Cost_{upfront,total} \\
= \$342M + \$270M \\
= \$611M
\end{gathered}
\] where: \[
PV_{OPEX} = OPEX_{ann} \times \frac{1 - (1+r)^{-T}}{r}
\] where: \[
\begin{gathered}
OPEX_{total} \\
= OPEX_{ann} + OPEX_{DIH,ann} \\
= \$18.9M + \$21.1M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{upfront,total} \\
= Cost_{upfront} + Cost_{DIH,init} \\
= \$40M + \$230M \\
= \$270M
\end{gathered}
\]
This yields the conservative estimate of 637:1 (95% CI: 569:1-790:1) ROI over 10 years.
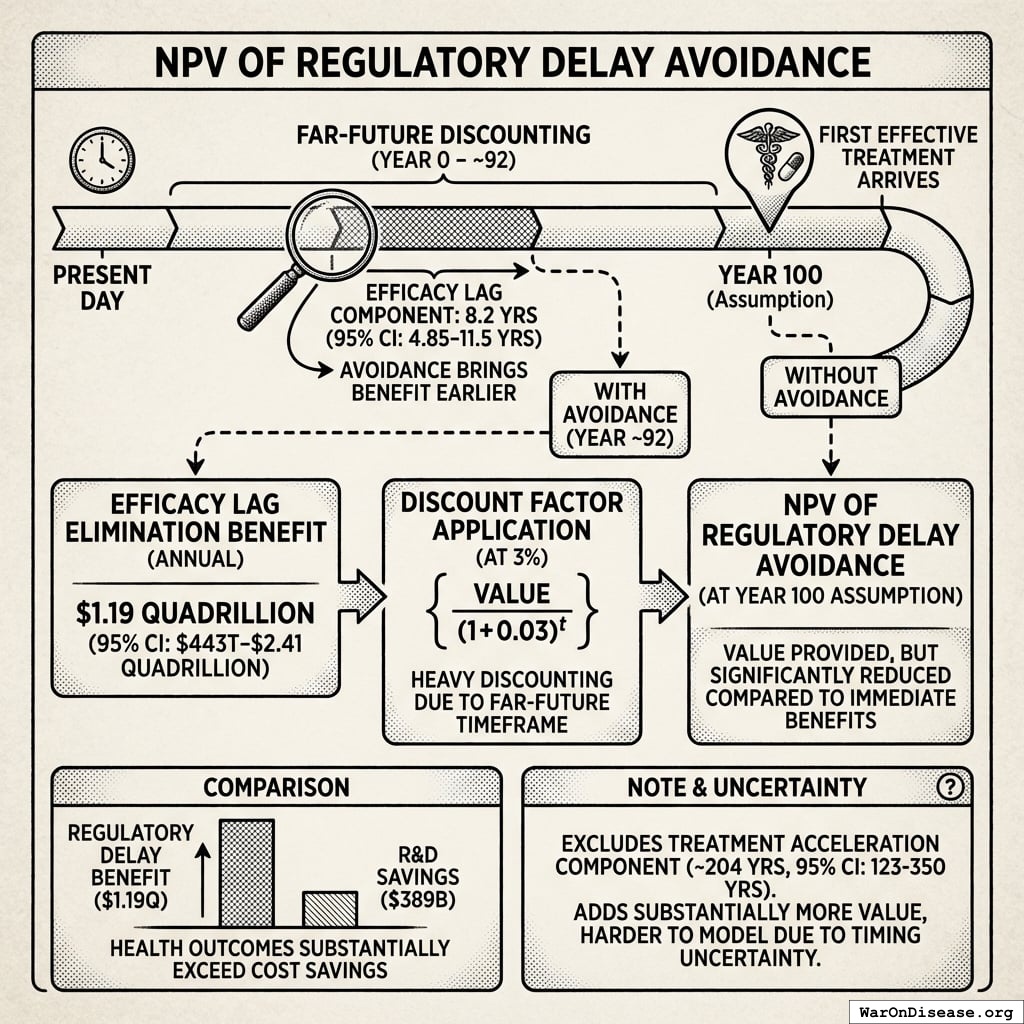
Important distinction: The NPV calculation above includes only annual recurring R&D savings. However, the cost per DALY calculations below do include the full ~212 years (95% CI: 135 years-355 years) average timeline shift (treatment acceleration + efficacy lag elimination), as this represents the primary health benefit. See Regulatory Mortality Analysis.
For the framework’s cost per health benefit averted (using the full ~212 years (95% CI: 135 years-355 years) average timeline shift):
Cost per DALY averted: $0.0018 (95% CI: $0.0007-$0.0041)
This represents $0.0018 (95% CI: $0.0007-$0.0041) per year of healthy life gained. This extremely low cost per DALY, combined with net economic benefits that exceed costs, qualifies this as a cost-saving intervention under model assumptions. Standard willingness-to-pay thresholds are $50K-$150K (95% CI: $100K-$199K)91 per QALY; cost-saving interventions are generally prioritized regardless of threshold.
NPV of Regulatory Delay Avoidance
The conservative NPV above excludes the benefit from eliminating the regulatory delay. This section calculates the NPV of just the efficacy lag component (8.2 years (95% CI: 4.85 years-11.5 years)) - a subset of the full ~212 years (95% CI: 135 years-355 years) timeline shift.
Assumption: We assume diseases receive first effective treatments 100 years in the future on average. If first effective treatments arrive at year 100, eliminating the regulatory delay brings them 8.2 years (95% CI: 4.85 years-11.5 years) earlier. Far-future discounting dramatically reduces NPV compared to immediate benefits, but the delay avoidance still provides value.
The NPV of regulatory delay avoidance (assuming average time to first effective treatment of 100 years):
Using the efficacy lag elimination benefit of $1.19 quadrillion (95% CI: $443T-$2.41 quadrillion), applied across 8.2 years (95% CI: 4.85 years-11.5 years) with future discounting at 3%.
This yields an NPV assuming first effective treatments are discovered 100 years in the future on average. The discount factor at year ~92 (when benefits begin) makes far-future benefits much smaller than if they occurred immediately.
Note: This NPV calculation covers only the efficacy lag component (8.2 years (95% CI: 4.85 years-11.5 years)). The treatment acceleration component (~204 years (95% CI: 123 years-350 years) on average) would add substantially more value, but is harder to model with NPV due to uncertainty in when each disease receives its first treatment.
Comparison: The regulatory delay avoidance benefit ($1.19 quadrillion (95% CI: $443T-$2.41 quadrillion) annually) is substantially larger than the conservative R&D-only benefit ($389B (95% CI: $327B-$485B):1 ROI), demonstrating that health outcomes substantially exceed cost savings even with far-future discounting. Note: These are separate benefit streams; the delay avoidance benefit does not include R&D savings.
Why this matters: Eliminating the regulatory delay still provides value even if first effective treatments are 100 years away on average, but far-future discounting means the NPV is much smaller. The actual value depends on when diseases actually receive first effective treatments, which varies by disease category. Some may receive treatments in 10-20 years (moderate discounting), others in 50-100+ years (heavy discounting). The 100-year assumption is conservative for many diseases that may take decades to treat effectively.
Quality-Adjusted Life Year (QALY) Valuation
QALYs represent the standard metric in health economics for comparing health interventions across different conditions and treatment modalities. One QALY equals one year of life in perfect health.
QALY Calculation Model
The total DALYs averted (565 billion DALYs (95% CI: 361 billion DALYs-877 billion DALYs)) from the ~212 years (95% CI: 135 years-355 years) timeline shift derives from two complementary mechanisms:
- Efficacy Lag Elimination (8.2 years (95% CI: 4.85 years-11.5 years)): Treatments reach patients immediately after Phase I safety, rather than waiting for Phase II/III efficacy trials
- Trial Capacity Expansion (204 years (95% CI: 123 years-350 years) average): 12.3x (95% CI: 4.19x-61.3x) more trials running in parallel accelerates discovery of first treatments for untreated diseases
\[
\begin{gathered}
DALYs_{max} \\
= DALYs_{global,ann} \times Pct_{avoid,DALY} \times T_{accel,max} \\
= 2.88B \times 92.6\% \times 212 \\
= 565B
\end{gathered}
\] where: \[
T_{accel,max} = T_{accel} + T_{lag} = 204 + 8.2 = 212
\] where: \[
\begin{gathered}
T_{accel} \\
= T_{first,SQ} \times \left(1 - \frac{1}{k_{capacity}}\right) \\
= 222 \times \left(1 - \frac{1}{12.3}\right) \\
= 204
\end{gathered}
\] where: \[
\begin{gathered}
T_{first,SQ} \\
= T_{queue,SQ} \times 0.5 \\
= 443 \times 0.5 \\
= 222
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\]
These benefits flow through three distinct channels:
A. Accelerated Development of Existing Pipeline Drugs
Health gains from bringing effective treatments to patients faster through shortened development and approval timelines:
B. Improved Preventative Care via Real-World Evidence
Value of using comprehensive data to optimize preventative care and treatment effectiveness:
C. Enabling Research for Previously Untreatable Diseases
Transformative potential to create viable research pathways for conditions ignored due to high trial costs:
QALY Valuation: Standard economic valuations range from $50K-$150K (95% CI: $100K-$199K)91 per QALY. This analysis uses conservative mid-range values.
The distribution below shows the uncertainty range in total DALYs averted from the combined timeline shift (efficacy lag elimination + trial capacity expansion), based on Monte Carlo simulation of input parameter uncertainty:
Simulation Results Summary: Total DALYs from Elimination of Efficacy Lag Plus Earlier Treatment Discovery from Higher Trial Throughput
| Baseline (deterministic) |
565 billion |
| Mean (expected value) |
610 billion |
| Median (50th percentile) |
614 billion |
| Standard Deviation |
148 billion |
| 90% Range (5th-95th percentile) |
[361 billion, 877 billion] |
The histogram shows the distribution of Total DALYs from Elimination of Efficacy Lag Plus Earlier Treatment Discovery from Higher Trial Throughput across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
For detailed DALY calculation methodology, see Regulatory Mortality Analysis.
Economist Verification: Complete Derivation Chains
This section provides step-by-step derivations for all headline claims, enabling independent verification. All intermediate values are linked to their source parameters in Parameters and Calculations.
Current System Baseline:
The trial capacity multiplier determines how many more trials can be run with reallocated funding:
Step 1: Calculate patients fundable annually
\[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\]
Step 2: Compare to current capacity
Step 3: Calculate multiplier
\[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\]
Step 4: Cumulative Research Impact (20-year horizon)
\[
\begin{gathered}
Capacity_{20yr} \\
= k_{capacity} \times 20 \\
= 12.3 \times 20 \\
= 246
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\]
The timeline shift combines two independent effects:
Component A: Treatment Acceleration from Trial Capacity
Step 1: Status quo time to explore therapeutic search space
\[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\]
Step 2: Expected time to first treatment
Step 3: Accelerated treatment timeline
With 12.3x (95% CI: 4.19x-61.3x) capacity, the search space is explored 12.3x (95% CI: 4.19x-61.3x) faster. The average disease receives treatment 204 years (95% CI: 123 years-350 years) earlier:
\[
\begin{gathered}
T_{accel} \\
= T_{first,SQ} \times \left(1 - \frac{1}{k_{capacity}}\right) \\
= 222 \times \left(1 - \frac{1}{12.3}\right) \\
= 204
\end{gathered}
\] where: \[
\begin{gathered}
T_{first,SQ} \\
= T_{queue,SQ} \times 0.5 \\
= 443 \times 0.5 \\
= 222
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\]
Component B: Efficacy Lag Elimination
Post-safety regulatory delay: 8.2 years (95% CI: 4.85 years-11.5 years) (BIO 2021: 10.5 years to market minus 2.3 years Phase I)
Total Timeline Shift
\[
T_{accel,max} = T_{accel} + T_{lag} = 204 + 8.2 = 212
\] where: \[
\begin{gathered}
T_{accel} \\
= T_{first,SQ} \times \left(1 - \frac{1}{k_{capacity}}\right) \\
= 222 \times \left(1 - \frac{1}{12.3}\right) \\
= 204
\end{gathered}
\] where: \[
\begin{gathered}
T_{first,SQ} \\
= T_{queue,SQ} \times 0.5 \\
= 443 \times 0.5 \\
= 222
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\]
Step 1: Identify annual DALY burden
Step 2: Determine avoidable fraction
- Eventually avoidable with biomedical research: 92.6% (95% CI: 50%-98%)
- Fundamentally unavoidable (accidents): 7.37%
Assumption justification (92.6% (95% CI: 50%-98%) avoidable): This represents the theoretical ceiling of what is biologically addressable, not what is currently preventable. It excludes only fundamentally unavoidable causes (primarily accidents, which cannot be addressed by medical research). Conservative estimates of current preventability (20-30%) are much lower because they measure what we can do today, not what is scientifically possible with sufficient research over decades.
Step 3: Calculate DALYs averted
\[
\begin{gathered}
DALYs_{max} \\
= DALYs_{global,ann} \times Pct_{avoid,DALY} \times T_{accel,max} \\
= 2.88B \times 92.6\% \times 212 \\
= 565B
\end{gathered}
\] where: \[
T_{accel,max} = T_{accel} + T_{lag} = 204 + 8.2 = 212
\] where: \[
\begin{gathered}
T_{accel} \\
= T_{first,SQ} \times \left(1 - \frac{1}{k_{capacity}}\right) \\
= 222 \times \left(1 - \frac{1}{12.3}\right) \\
= 204
\end{gathered}
\] where: \[
\begin{gathered}
T_{first,SQ} \\
= T_{queue,SQ} \times 0.5 \\
= 443 \times 0.5 \\
= 222
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\]
Step 1: Identify one-time implementation cost
- Treaty implementation cost: $1B
- Referendum: $250M
- Lobbying: $650M
- Reserve: $100M
Step 2: Calculate cost per DALY
\[
\begin{gathered}
Cost_{treaty,DALY} \\
= \frac{Cost_{campaign}}{DALYs_{max}} \\
= \frac{\$1B}{565B} \\
= \$0.00177
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{campaign} \\
= Budget_{viral,base} + Budget_{lobby,treaty} \\
+ Budget_{reserve} \\
= \$250M + \$650M + \$100M \\
= \$1B
\end{gathered}
\] where: \[
\begin{gathered}
DALYs_{max} \\
= DALYs_{global,ann} \times Pct_{avoid,DALY} \times T_{accel,max} \\
= 2.88B \times 92.6\% \times 212 \\
= 565B
\end{gathered}
\] where: \[
T_{accel,max} = T_{accel} + T_{lag} = 204 + 8.2 = 212
\] where: \[
\begin{gathered}
T_{accel} \\
= T_{first,SQ} \times \left(1 - \frac{1}{k_{capacity}}\right) \\
= 222 \times \left(1 - \frac{1}{12.3}\right) \\
= 204
\end{gathered}
\] where: \[
\begin{gathered}
T_{first,SQ} \\
= T_{queue,SQ} \times 0.5 \\
= 443 \times 0.5 \\
= 222
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\]
Comparison: Malaria bed nets cost $89 (95% CI: $78-$100)/DALY - this intervention is 50.3kx (95% CI: 23.7kx-111.7kx) more cost-effective.
The conservative ROI uses only R&D cost savings, ignoring all health benefits:
Step 1: Calculate annual R&D savings
\[
\begin{gathered}
Benefit_{RD,ann} \\
= Spending_{trials} \times Reduce_{pct} \\
= \$60B \times 97.7\% \\
= \$58.6B
\end{gathered}
\] where: \[
\begin{gathered}
Reduce_{pct} \\
= 1 - \frac{Cost_{pragmatic,pt}}{Cost_{P3,pt}} \\
= 1 - \frac{\$929}{\$41K} \\
= 97.7\%
\end{gathered}
\]
Step 2: Calculate NPV of benefits (10-year horizon)
\[
\begin{gathered}
NPV_{RD} \\
= \sum_{t=1}^{10} \frac{Savings_{RD,ann} \times \frac{\min(t,5)}{5}}{(1+r)^t}
\end{gathered}
\]
Step 3: Calculate NPV of costs
Step 4: Calculate ROI
\[
\begin{gathered}
ROI_{RD} \\
= \frac{NPV_{RD}}{Cost_{dFDA,total}} \\
= \frac{\$389B}{\$611M} \\
= 637
\end{gathered}
\] where: \[
\begin{gathered}
NPV_{RD} \\
= \sum_{t=1}^{10} \frac{Savings_{RD,ann} \times \frac{\min(t,5)}{5}}{(1+r)^t}
\end{gathered}
\] where: \[
\begin{gathered}
Savings_{RD,ann} \\
= Benefit_{RD,ann} - OPEX_{dFDA} \\
= \$58.6B - \$40M \\
= \$58.6B
\end{gathered}
\] where: \[
\begin{gathered}
Benefit_{RD,ann} \\
= Spending_{trials} \times Reduce_{pct} \\
= \$60B \times 97.7\% \\
= \$58.6B
\end{gathered}
\] where: \[
\begin{gathered}
Reduce_{pct} \\
= 1 - \frac{Cost_{pragmatic,pt}}{Cost_{P3,pt}} \\
= 1 - \frac{\$929}{\$41K} \\
= 97.7\%
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{dFDA,total} \\
= PV_{OPEX} + Cost_{upfront,total} \\
= \$342M + \$270M \\
= \$611M
\end{gathered}
\] where: \[
PV_{OPEX} = OPEX_{ann} \times \frac{1 - (1+r)^{-T}}{r}
\] where: \[
\begin{gathered}
OPEX_{total} \\
= OPEX_{ann} + OPEX_{DIH,ann} \\
= \$18.9M + \$21.1M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{upfront,total} \\
= Cost_{upfront} + Cost_{DIH,init} \\
= \$40M + \$230M \\
= \$270M
\end{gathered}
\]
The complete ROI includes the full timeline shift health benefits:
Step 1: Economic value of timeline shift
\[
\begin{gathered}
Value_{max} \\
= DALYs_{max} \times Value_{QALY} \\
= 565B \times \$150K \\
= \$84800T
\end{gathered}
\] where: \[
\begin{gathered}
DALYs_{max} \\
= DALYs_{global,ann} \times Pct_{avoid,DALY} \times T_{accel,max} \\
= 2.88B \times 92.6\% \times 212 \\
= 565B
\end{gathered}
\] where: \[
T_{accel,max} = T_{accel} + T_{lag} = 204 + 8.2 = 212
\] where: \[
\begin{gathered}
T_{accel} \\
= T_{first,SQ} \times \left(1 - \frac{1}{k_{capacity}}\right) \\
= 222 \times \left(1 - \frac{1}{12.3}\right) \\
= 204
\end{gathered}
\] where: \[
\begin{gathered}
T_{first,SQ} \\
= T_{queue,SQ} \times 0.5 \\
= 443 \times 0.5 \\
= 222
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\]
QALY Valuation Justification ($150K (95% CI: $100K-$199K)): This uses standard US economic valuations. WHO recommends $50K-$150K (95% CI: $100K-$199K) per QALY for cost-effectiveness thresholds in high-income countries. The $150K (95% CI: $100K-$199K) value reflects revealed preferences from regulatory decisions (EPA, FDA), wage-risk tradeoffs, and health insurance willingness-to-pay studies. International analyses often use lower thresholds ($50-100K), which would reduce the ROI proportionally but not change the cost-saving classification.
Step 2: Calculate ROI
\[
\begin{gathered}
ROI_{max} \\
= \frac{Value_{max}}{Cost_{campaign}} \\
= \frac{\$84800T}{\$1B} \\
= 84.8M
\end{gathered}
\] where: \[
\begin{gathered}
Value_{max} \\
= DALYs_{max} \times Value_{QALY} \\
= 565B \times \$150K \\
= \$84800T
\end{gathered}
\] where: \[
\begin{gathered}
DALYs_{max} \\
= DALYs_{global,ann} \times Pct_{avoid,DALY} \times T_{accel,max} \\
= 2.88B \times 92.6\% \times 212 \\
= 565B
\end{gathered}
\] where: \[
T_{accel,max} = T_{accel} + T_{lag} = 204 + 8.2 = 212
\] where: \[
\begin{gathered}
T_{accel} \\
= T_{first,SQ} \times \left(1 - \frac{1}{k_{capacity}}\right) \\
= 222 \times \left(1 - \frac{1}{12.3}\right) \\
= 204
\end{gathered}
\] where: \[
\begin{gathered}
T_{first,SQ} \\
= T_{queue,SQ} \times 0.5 \\
= 443 \times 0.5 \\
= 222
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{campaign} \\
= Budget_{viral,base} + Budget_{lobby,treaty} \\
+ Budget_{reserve} \\
= \$250M + \$650M + \$100M \\
= \$1B
\end{gathered}
\]
Step 1: Identify daily mortality
Step 2: Apply avoidable fraction
- Eventually avoidable: 92.6% (95% CI: 50%-98%)
Step 3: Calculate lives saved from timeline shift
\[
\begin{gathered}
Lives_{max} \\
= Deaths_{disease,daily} \times T_{accel,max} \times 338 \\
= 150{,}000 \times 212 \times 338 \\
= 10.7B
\end{gathered}
\] where: \[
T_{accel,max} = T_{accel} + T_{lag} = 204 + 8.2 = 212
\] where: \[
\begin{gathered}
T_{accel} \\
= T_{first,SQ} \times \left(1 - \frac{1}{k_{capacity}}\right) \\
= 222 \times \left(1 - \frac{1}{12.3}\right) \\
= 204
\end{gathered}
\] where: \[
\begin{gathered}
T_{first,SQ} \\
= T_{queue,SQ} \times 0.5 \\
= 443 \times 0.5 \\
= 222
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\]
Regulatory Delay Elimination Derivation
Step 1: Lives Saved from Lag Elimination
\[
\begin{gathered}
Deaths_{lag} \\
= T_{lag} \times Deaths_{disease,daily} \times 338 \\
= 8.2 \times 150{,}000 \times 338 \\
= 416M
\end{gathered}
\]
Step 2: Economic Value of Lag Elimination
\[
\begin{gathered}
Value_{lag} \\
= DALYs_{lag} \times Value_{QALY} \\
= 7.94B \times \$150K \\
= \$1190T
\end{gathered}
\] where: \[
DALYs_{lag} = YLL_{lag} + YLD_{lag} = 7.07B + 873M = 7.94B
\] where: \[
\begin{gathered}
YLL_{lag} \\
= Deaths_{lag} \times (LE_{global} - Age_{death,delay}) \\
= 416M \times (79 - 62) \\
= 7.07B
\end{gathered}
\] where: \[
\begin{gathered}
Deaths_{lag} \\
= T_{lag} \times Deaths_{disease,daily} \times 338 \\
= 8.2 \times 150{,}000 \times 338 \\
= 416M
\end{gathered}
\] where: \[
\begin{gathered}
YLD_{lag} \\
= Deaths_{lag} \times T_{suffering} \times DW_{chronic} \\
= 416M \times 6 \times 0.35 \\
= 873M
\end{gathered}
\]
Annual Recurring Benefits Derivation
\[
\begin{gathered}
Benefit_{peace+RD} \\
= Benefit_{peace,soc} + Benefit_{RD,ann} \\
= \$114B + \$58.6B \\
= \$172B
\end{gathered}
\] where: \[
\begin{gathered}
Benefit_{peace,soc} \\
= Cost_{war,total} \times Reduce_{treaty} \\
= \$11.4T \times 1\% \\
= \$114B
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{war,total} \\
= Cost_{war,direct} + Cost_{war,indirect} \\
= \$7.66T + \$3.7T \\
= \$11.4T
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{war,direct} \\
= Loss_{life,conflict} + Damage_{infra,total} \\
+ Disruption_{trade} + Spending_{mil} \\
= \$2.45T + \$1.88T + \$616B + \$2.72T \\
= \$7.66T
\end{gathered}
\] where: \[
\begin{gathered}
Loss_{life,conflict} \\
= Cost_{combat,human} + Cost_{state,human} \\
+ Cost_{terror,human} \\
= \$2.34T + \$27B + \$83B \\
= \$2.45T
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{combat,human} \\
= Deaths_{combat} \times VSL \\
= 234{,}000 \times \$10M \\
= \$2.34T
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{state,human} \\
= Deaths_{state} \times VSL \\
= 2{,}700 \times \$10M \\
= \$27B
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{terror,human} \\
= Deaths_{terror} \times VSL \\
= 8{,}300 \times \$10M \\
= \$83B
\end{gathered}
\] where: \[
\begin{gathered}
Damage_{infra,total} \\
= Damage_{comms} + Damage_{edu} + Damage_{energy} \\
+ Damage_{health} + Damage_{transport} + Damage_{water} \\
= \$298B + \$234B + \$422B + \$166B + \$487B + \$268B \\
= \$1.88T
\end{gathered}
\] where: \[
\begin{gathered}
Disruption_{trade} \\
= Disruption_{currency} + Disruption_{energy} \\
+ Disruption_{shipping} + Disruption_{supply} \\
= \$57.4B + \$125B + \$247B + \$187B \\
= \$616B
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{war,indirect} \\
= Damage_{env} + Loss_{growth,mil} + Loss_{capital,conflict} \\
+ Cost_{psych} + Cost_{refugee} + Cost_{vet} \\
= \$100B + \$2.72T + \$300B + \$232B + \$150B + \$200B \\
= \$3.7T
\end{gathered}
\] where: \[
\begin{gathered}
Benefit_{RD,ann} \\
= Spending_{trials} \times Reduce_{pct} \\
= \$60B \times 97.7\% \\
= \$58.6B
\end{gathered}
\] where: \[
\begin{gathered}
Reduce_{pct} \\
= 1 - \frac{Cost_{pragmatic,pt}}{Cost_{P3,pt}} \\
= 1 - \frac{\$929}{\$41K} \\
= 97.7\%
\end{gathered}
\]
Verification Summary
| Trial Capacity |
12.3x (95% CI: 4.19x-61.3x) |
Patients fundable ÷ current slots |
Funding, trial cost, current capacity |
| Timeline Shift |
212 years (95% CI: 135 years-355 years) |
Treatment acceleration + efficacy lag |
Discovery capacity model, multiplier, regulatory data |
| DALYs Averted |
565 billion DALYs (95% CI: 361 billion DALYs-877 billion DALYs) |
DALY burden × avoidable × shift |
WHO GBD, avoidability assumption |
| Cost/DALY |
$0.0018 (95% CI: $0.0007-$0.0041) |
Implementation cost ÷ DALYs |
Implementation budget, DALYs |
| ROI (Conservative) |
637:1 (95% CI: 569:1-790:1) |
NPV benefits ÷ NPV costs |
Trial savings, discount rate |
| ROI (Complete) |
84.8M:1 (95% CI: 46.6M:1-144M:1) |
Economic value ÷ implementation cost |
QALY valuation, timeline shift |
| Lives Saved |
10.7 billion deaths (95% CI: 7.39 billion deaths-16.2 billion deaths) |
Daily deaths × avoidable × shift |
WHO mortality, timeline shift |
| Delay Lives |
416 million deaths (95% CI: 225 million deaths-630 million deaths) |
Daily deaths × lag × avoidable |
WHO mortality, lag years |
| Delay Value |
$1.19 quadrillion (95% CI: $443T-$2.41 quadrillion) |
Delay DALYs × QALY Value |
Delay DALYs, QALY ($150k) |
Sensitivity to key assumptions: The tornado diagrams throughout this document show that results are most sensitive to: (1) timeline shift duration, (2) QALY valuation, and (3) eventually avoidable percentage. Even under conservative parameter assumptions (lower timeline shift, lower QALY values, lower avoidability), the intervention remains cost-saving.
For complete parameter definitions, uncertainty ranges, and Monte Carlo distributions, see Parameters and Calculations.
Counterfactual Baseline Specification
This cost-effectiveness analysis uses the status quo as the baseline counterfactual: military spending continues at current levels ($2.72T48 annually) and is allocated to traditional military purposes. Under this baseline, the $27.2B redirected to pragmatic clinical trials infrastructure would otherwise remain in military budgets.
Alternative counterfactual scenarios include:
Military R&D continuation: The $27.2B continues funding military research and development, potentially yielding civilian technology spillovers (e.g., GPS, internet protocols, materials science advances). This scenario is partially addressed in the peace dividend calculations, which acknowledge that military spending generates economic multiplier effects of 0.5-1.0× compared to pragmatic clinical trial multipliers of 2.0-3.0×.
Return to taxpayers: Funds are returned via tax cuts, enabling private consumption and investment. Under this scenario, the opportunity cost equals the weighted average return on private capital (approximately 3% annually in developed economies).
Alternative government priorities: Reallocation to other public investments such as infrastructure, education, or climate mitigation. Each alternative use would require separate cost-benefit analysis to determine relative efficiency.
Methodological note on baseline selection: The economically rigorous baseline is the “next best alternative use” rather than “status quo continuation.” However, identifying the single next-best alternative requires comprehensive comparison across all possible uses of public funds, which exceeds the scope of this analysis. This analysis therefore focuses on the conditional benefits of the system: the health and economic gains achievable by redirecting $27.2B from military to medical research infrastructure.
Conservative interpretation: Even if alternative uses generate positive economic value, a global pragmatic trial system exhibits dominant intervention characteristics (cost-saving: $0.0018 (95% CI: $0.0007-$0.0041) per DALY), indicating it saves costs while improving health outcomes. Under standard cost-effectiveness frameworks, dominant interventions are unconditionally recommended regardless of alternative uses, as they represent free gains in both dimensions (reduced costs and improved health).
Peace Dividend Calculation Methodology
Economic benefits of reduced military spending
- Direct fiscal savings (Cash): $27.2B available for productive investment. This is the floor.
- Diplomatic De-escalation (Upside): Reduced conflict-related economic damage (trade disruption, infrastructure destruction, refugee costs).
Opportunity Cost & Signal Value: The argument isn’t just that 1% less budget stops 1% of bullets linearly. It’s that 1% redirected to shared survival goals (curing disease) acts as a confidence-building measure (CBM) in arms control theory. It signals a shift from zero-sum competition to positive-sum cooperation.
Conservative estimate: Analysis uses $114B (95% CI: $90.1B-$141B) annual peace dividend. Even if conflict intensity doesn’t drop linearly, the $27.2B annual cash reallocation is real. The ROI works on the cash alone; peace is a massive bonus.
War Costs Breakdown
| Direct Military Spending |
$2.72T48 |
SIPRI 2024 global military budgets (source)61 |
| Infrastructure Destruction |
$1.88T (95% CI: $1.37T-$2.47T) |
Transportation, energy, communications, water, education, healthcare facilities |
| Human Life Losses |
$2.45T (95% CI: $1.31T-$3.75T) |
245 thousand deaths/year (95% CI: 194 thousand deaths/year-302 thousand deaths/year) conflict deaths × $10M (95% CI: $5M-$15M)127 value of statistical life (conservative estimate) |
| Trade Disruption |
$616B (95% CI: $450B-$812B) |
Shipping, supply chains, energy prices, currency volatility |
| Lost Economic Growth |
$2.72T (95% CI: $1.90T-$3.80T)35 |
Opportunity cost of military spending vs. productive investment |
| Veteran Healthcare |
$200B (95% CI: $140B-$280B)40 |
Long-term medical care for conflict-related injuries |
| Refugee Support |
$150B (95% CI: $105B-$210B)38 |
108.4M displaced persons139 × $1,384/year38 |
| Environmental Damage |
$100B (95% CI: $70B-$140B)33 |
Environmental destruction, toxic contamination, restoration costs |
| Psychological Impact |
$232B (95% CI: $162B-$325B)37 |
PTSD treatment, mental health services, productivity loss |
| Lost Human Capital |
$300B (95% CI: $210B-$420B)36 |
Productive capacity lost from casualties and displacement |
| Total War Costs |
$11.4T (95% CI: $9.01T-$14.1T) |
Combined direct and indirect annual costs |
| 1% Reduction |
$114B (95% CI: $90.1B-$141B) |
Peace dividend from 1% treaty implementation |
This calculation methodology follows standard cost-of-conflict analysis frameworks used by the World Bank, IMF, and academic conflict economics research.
Note on confidence levels: The direct military spending reduction ($27.2B) has high confidence. The remaining conflict cost reductions assume proportional scaling (1% military spending → 1% conflict reduction) which lacks empirical validation. Conservative scenarios should use only direct fiscal savings; optimistic scenarios can include full peace dividend effects.
Sensitivity of peace dividend estimate: The tornado chart below shows which cost components have the largest impact on the total peace dividend. The primary drivers are infrastructure destruction costs and lost economic growth:
Confidence level separation: The peace dividend calculation separates into two components:
Direct fiscal savings (high confidence): $27.2B - The 1% reduction in military budgets ($27.2B) represents direct fiscal savings with high certainty. These funds are immediately available for reallocation.
Conflict reduction benefits (upside scenario): $86.4B (95% CI: $62.9B-$113B) - The remaining $86.4B (95% CI: $62.9B-$113B) models the benefits if conflict costs reduce proportionally. While the causal link between marginal budget cuts and conflict intensity is complex, the directionality is positive.
\[
\begin{gathered}
Savings_{conflict} \\
= Benefit_{peace,soc} - Funding_{treaty} \\
= \$114B - \$27.2B \\
= \$86.4B
\end{gathered}
\] where: \[
\begin{gathered}
Benefit_{peace,soc} \\
= Cost_{war,total} \times Reduce_{treaty} \\
= \$11.4T \times 1\% \\
= \$114B
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{war,total} \\
= Cost_{war,direct} + Cost_{war,indirect} \\
= \$7.66T + \$3.7T \\
= \$11.4T
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{war,direct} \\
= Loss_{life,conflict} + Damage_{infra,total} \\
+ Disruption_{trade} + Spending_{mil} \\
= \$2.45T + \$1.88T + \$616B + \$2.72T \\
= \$7.66T
\end{gathered}
\] where: \[
\begin{gathered}
Loss_{life,conflict} \\
= Cost_{combat,human} + Cost_{state,human} \\
+ Cost_{terror,human} \\
= \$2.34T + \$27B + \$83B \\
= \$2.45T
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{combat,human} \\
= Deaths_{combat} \times VSL \\
= 234{,}000 \times \$10M \\
= \$2.34T
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{state,human} \\
= Deaths_{state} \times VSL \\
= 2{,}700 \times \$10M \\
= \$27B
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{terror,human} \\
= Deaths_{terror} \times VSL \\
= 8{,}300 \times \$10M \\
= \$83B
\end{gathered}
\] where: \[
\begin{gathered}
Damage_{infra,total} \\
= Damage_{comms} + Damage_{edu} + Damage_{energy} \\
+ Damage_{health} + Damage_{transport} + Damage_{water} \\
= \$298B + \$234B + \$422B + \$166B + \$487B + \$268B \\
= \$1.88T
\end{gathered}
\] where: \[
\begin{gathered}
Disruption_{trade} \\
= Disruption_{currency} + Disruption_{energy} \\
+ Disruption_{shipping} + Disruption_{supply} \\
= \$57.4B + \$125B + \$247B + \$187B \\
= \$616B
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{war,indirect} \\
= Damage_{env} + Loss_{growth,mil} + Loss_{capital,conflict} \\
+ Cost_{psych} + Cost_{refugee} + Cost_{vet} \\
= \$100B + \$2.72T + \$300B + \$232B + \$150B + \$200B \\
= \$3.7T
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\]
Conservative interpretation: The direct fiscal savings ($27.2B annually) are certain. The “peace dividend” is treated as an upside scenario in the conservative case, ensuring the economic model doesn’t rely on optimistic geopolitical outcomes. The ROI remains positive on R&D savings alone.
Research Acceleration Mechanism
The 12.3x (95% CI: 4.19x-61.3x) research acceleration multiplier comes from the combination of multiple proven accelerators:
Faster Recruitment: The Oxford RECOVERY trial recruited 47,000+ patients across nearly 200 hospitals140, while 80% of traditional trials fail to meet enrollment timelines141. This speed comes from pragmatic eligibility (minimal exclusions142 vs. 86.1% excluded traditionally) and embedded recruitment in routine care.
Faster Completion: Pragmatic trials complete in 3-12 months instead of 3-5 years because patient subsidies flip economic incentives. Physicians gain revenue from trial participation rather than losing it, eliminating the perverse incentives that delay traditional trials.
Massive Parallelization: With more trials running simultaneously (vs. 10.0 thousand trials10 today), the framework achieves substantially more concurrent research. Universal patient participation makes this possible, as every doctor’s office becomes a trial site.
Higher Completion Rates: More of pragmatic trials complete (vs. 40%14 abandonment rate today) because patients are subsidized and physicians profit from participation.
These improvements compound multiplicatively to produce the 12.3x (95% CI: 4.19x-61.3x) acceleration used in this analysis. This is a conservative estimate accounting for implementation constraints, regulatory requirements, and gradual adoption.
Generalizability of Cost Savings: Critics regarding RECOVERY and ADAPTABLE as outliers should note that a systematic review of 64 embedded pragmatic clinical trials74 found a median cost per participant of just $97 (IQR $19–$478). High-cost traditional trials are necessary only for first-in-human safety testing. For the 9.50 million combinations unexplored combinations of already-safe compounds (repurposing), pragmatic protocols are sufficient, covering the vast majority (>90%) of the therapeutic search space.
Sensitivity of research acceleration estimate: The tornado chart below shows which input parameters have the largest impact on the trial capacity multiplier. The width of each bar shows how much the multiplier changes when that parameter varies across its uncertainty range:
Automating Friction, Not Judgment: The system operates as automated infrastructure analyzing time-series EHR data from electronic health records, wearables, and apps. The 12.3x (95% CI: 4.19x-61.3x) research acceleration does not require 12.3x (95% CI: 4.19x-61.3x) more Principal Investigators.
The bottleneck in clinical research isn’t “scientific genius”, we have plenty of underemployed PhDs. The bottleneck is “Data Friction”.
Currently, researchers spend up to 50% of their time143 on grants and administrative tasks. A decentralized FDA automates this overhead, liberating human judgment to focus on hypothesis generation and complex safety signal interpretation.
The TurboTax Analogy: Just as TurboTax wraps the complexity of federal, state, and local tax codes into a simple interface (users answer questions, it generates compliant filings), a global pragmatic trial system wraps the complexity of global regulatory bodies (FDA, EMA, PMDA, Health Canada, TGA, etc.) into a unified system. Researchers define their hypothesis and patient population; the system automatically:
- Generates IRB submissions for each jurisdiction
- Handles liability insurance and indemnification
- Creates compliant protocol documents for each agency
- Submits applications simultaneously to multiple regulatory bodies
- Aggregates real-world evidence into agency-specific formats
- Manages ongoing reporting requirements across jurisdictions
The system uses federated queries (data stays in EHR and consumer health app systems) rather than centralized databases, enabling analysis without data movement. Physicians continue normal clinical practice; the system automatically detects patterns, identifies treatment effects, and flags signals for peer review. This is fundamentally different from traditional research models that scale linearly with researcher headcount.
Treatment Discovery Through Therapeutic Space Exploration
The 12.3x (95% CI: 4.19x-61.3x) research acceleration transforms our ability to explore the vast therapeutic space where undiscovered treatments already exist.
The Unexplored Therapeutic Frontier
The fundamental problem isn’t that effective treatments are hard to discover. It’s that we’re barely looking. As documented in The Untapped Therapeutic Frontier:
- 9.50 million combinations plausible drug-disease combinations exist (9.50 thousand compounds (95% CI: 7.00 thousand compounds-12.0 thousand compounds) safe compounds × 1.00 thousand diseases (95% CI: 800 diseases-1.20 thousand diseases))
- <1% of these combinations have been tested
- Only 12% of the human interactome has ever been targeted by drugs
- 30% of approved drugs gain new indications, proving undiscovered uses exist
\[
\begin{gathered}
N_{combos} \\
= N_{safe} \times N_{diseases,trial} \\
= 9{,}500 \times 1{,}000 \\
= 9.5M
\end{gathered}
\]
Effective treatments likely already exist among tested-safe compounds. We just haven’t looked.
Current Exploration Rate vs. Therapeutic Space
Under the status quo:
\[
\begin{gathered}
T_{first,SQ} \\
= T_{queue,SQ} \times 0.5 \\
= 443 \times 0.5 \\
= 222
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\]
This calculation is empirically grounded: only ~5% of the 7.00 thousand diseases (95% CI: 6.00 thousand diseases-10.0 thousand diseases) rare diseases have FDA-approved treatments after 40+ years of the Orphan Drug Act. At the current rate of 15 diseases/year (95% CI: 8 diseases/year-30 diseases/year) diseases/year getting first treatments, most of the therapeutic space remains permanently unexplored.
With framework implementation:
\[
\begin{gathered}
Treatments_{dFDA,ann} \\
= Treatments_{new,ann} \times k_{capacity} \\
= 15 \times 12.3 \\
= 185
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\]
\[
\begin{gathered}
T_{queue,dFDA} \\
= \frac{T_{queue,SQ}}{k_{capacity}} \\
= \frac{443}{12.3} \\
= 36
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\]
Additionally, eliminating the 8.2 years (95% CI: 4.85 years-11.5 years) efficacy lag means discovered treatments reach patients immediately. The total timeline shift is 212 years (95% CI: 135 years-355 years) (discovery acceleration + efficacy lag elimination).
\[
T_{accel,max} = T_{accel} + T_{lag} = 204 + 8.2 = 212
\] where: \[
\begin{gathered}
T_{accel} \\
= T_{first,SQ} \times \left(1 - \frac{1}{k_{capacity}}\right) \\
= 222 \times \left(1 - \frac{1}{12.3}\right) \\
= 204
\end{gathered}
\] where: \[
\begin{gathered}
T_{first,SQ} \\
= T_{queue,SQ} \times 0.5 \\
= 443 \times 0.5 \\
= 222
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\]
Note: Valley of death rescue (1.4x) adds more drug candidates to the pipeline, further expanding the explorable therapeutic space.
\[
k_{rescue} = Attrition_{valley} + 1 = 40\% + 1 = 1.4
\]
This acceleration applies across all diseases, not just well-funded ones. The current system prioritizes diseases with commercial potential; the framework’s universal trial infrastructure removes economic barriers that leave rare and neglected diseases permanently unexplored.
Addressing the Returns Question: Diminishing, Linear, or Compounding?
A common objection is that “more trials won’t produce proportionally more treatments,” the diminishing returns hypothesis. This deserves serious consideration, but the evidence suggests the opposite may be true.
Important distinction: Bloom et al. (2020)144 document declining research productivity (~5% annually across industries), but this measures idea productivity (breakthroughs per researcher-year). This intervention targets a different margin: trial execution efficiency (cost per patient enrolled, completion rates, recruitment speed). Streamlining data collection is not the same as discovering new biology.
Why Diminishing Returns Is Unlikely (We Haven’t Started Looking)
The diminishing returns objection assumes we’ve exhausted low-hanging fruit. But we’ve barely begun:
- Single compounds alone: 9.50 million combinations possible combinations of known safe compounds × diseases. At current trial capacity, systematically testing these would take 2.88 thousand years (95% CI: 2.45 thousand years-3.43 thousand years). We won’t finish until the year 5000.
\[
\begin{gathered}
T_{explore,safe} \\
= \frac{N_{combos}}{Trials_{ann,curr}} \\
= \frac{9.5M}{3{,}300} \\
= 2{,}880
\end{gathered}
\] where: \[
\begin{gathered}
N_{combos} \\
= N_{safe} \times N_{diseases,trial} \\
= 9{,}500 \times 1{,}000 \\
= 9.5M
\end{gathered}
\]
- Combination therapies expand the space: Modern medicine relies on multi-drug regimens (oncology, HIV, cardiology). Pairwise combinations of safe compounds create 45.1 billion combinations possibilities, requiring 13.7 million years (95% CI: 11.6 million years-16.3 million years) at current pace, longer than Homo sapiens has existed.
\[
\begin{gathered}
Space_{combo} \\
= N_{combo} \times N_{diseases,trial} \\
= 45.1M \times 1{,}000 \\
= 45.1B
\end{gathered}
\]
Repurposing success proves effective treatments exist: 30% of approved drugs gain new indications, demonstrating the unexplored space contains discoveries.
Most biology is untargeted: Only 12% of the human interactome has been targeted. We’re ignoring 88% of our own biology.
Systematic search yields rapid discoveries: The Oxford RECOVERY trial discovered multiple effective COVID treatments in months because it looked systematically. This pattern replicates across the 108+ pragmatic trials in the Harvard meta-analysis132.
See The Untapped Therapeutic Frontier for the complete tiered analysis of therapeutic space.
You cannot have diminishing returns when you’ve barely started.
The Case for Compounding Returns
Platform technologies may actually produce increasing returns per trial over time:
Expanding the candidate pipeline:
- mRNA platforms: COVID vaccines demonstrated mRNA can be designed in days. This platform applies to cancer, infectious diseases, and potentially genetic disorders, vastly expanding testable candidates
- AI drug discovery: Machine learning models increasingly predict drug-target interactions, enabling smarter trial selection. DeepMind’s AlphaFold solved protein structure prediction; similar approaches will prioritize high-probability combinations
- Epigenetic reprogramming: Yamanaka factors demonstrated cellular reprogramming. As this technology matures, entirely new therapeutic modalities become testable
- Gene therapy platforms: AAV vectors, plasmid delivery, and CRISPR-based approaches create thousands of new candidate therapies annually
Learning effects that improve success rates:
- Predictive analytics: Each completed trial generates data that improves predictions for future trials. As the framework accumulates outcomes across millions of patients, machine learning models will increasingly identify which drug-disease combinations merit testing
- Network pharmacology: Understanding how drugs affect biological networks (not just single targets) reveals unexpected therapeutic applications. More data = better network models = higher hit rates
- Biomarker discovery: Large-scale trial data identifies patient subpopulations who respond to specific treatments, enabling precision targeting that increases trial success rates
- Failure analysis: Systematically studying why trials fail (wrong dose, wrong population, wrong endpoint) improves future trial design
- Biological model refinement: Every trial (success or failure) teaches us how human biology responds to interventions. This cumulative knowledge improves our mechanistic understanding of disease pathways, enabling increasingly accurate prediction of which candidates will work. The ratio of effective treatments per trial should increase over time, not decrease.
Mathematical Framework: When Would Diminishing Returns Dominate?
We can formalize the competing models to identify when diminishing returns would actually matter.
Model 1: Linear (Baseline)
\[
T_{discovered} = k_0 \cdot N_{trials}
\]
Where \(k_0\) is the constant discovery rate (effective treatments per trial). This assumes the therapeutic space is sampled uniformly at random.
Model 2: Diminishing Returns (Pessimistic)
As we exhaust the therapeutic space, the hit rate decreases:
\[
k_{dim}(s) = k_0 \cdot (1 - s)
\]
Where \(s = S_{explored}/S_{total}\) is the fraction of therapeutic space already tested. At current exploration (\(s < 0.01\)), this gives \(k_{dim} \approx 0.99 \cdot k_0\), virtually identical to linear.
Model 3: Learning/Compounding (Optimistic)
Each trial improves our biological models, increasing future hit rates:
\[
k_{learn}(n) = k_0 \cdot \left(1 + \alpha \cdot \ln(1 + n)\right)
\]
Where \(\alpha\) is the learning coefficient and \(n\) is cumulative trials completed. Even modest learning (\(\alpha = 0.1\)) with 100,000 trials yields \(k_{learn} \approx 2.15 \cdot k_0\).
Model 4: Combined (Realistic)
Both effects operate simultaneously:
\[
k_{combined}(s, n) = k_0 \cdot (1 - s) \cdot \left(1 + \alpha \cdot \ln(1 + n)\right)
\]
The Crossover Point: When Does Depletion Dominate Learning?
Diminishing returns dominates when the depletion factor exceeds the learning factor:
\[
(1 - s) < \frac{1}{1 + \alpha \cdot \ln(1 + n)}
\]
Solving for the critical exploration fraction:
\[
s_{crossover} = 1 - \frac{1}{1 + \alpha \cdot \ln(1 + n)}
\]
Numerical Analysis:
| 0.05 (weak) |
100,000 |
37% |
| 0.10 (modest) |
100,000 |
53% |
| 0.15 (strong) |
100,000 |
63% |
| 0.10 (modest) |
1,000,000 |
61% |
Interpretation: Even with weak learning effects, diminishing returns only dominates after exploring 37%+ of therapeutic space. With modest learning, the crossover occurs at 53%+ exploration.
Timeline to Crossover:
At current exploration of 0.342% (95% CI: 0.21%-0.514%) (<1%), reaching the 53% crossover would require:
For combination therapies (45.1 billion combinations), reaching 53% exploration would take:
- Current pace: ~7 million years
- With framework: ~600,000 years
Conclusion: For any plausible planning horizon, learning effects dominate. Diminishing returns is a theoretical concern for civilizations operating on multi-century timescales, not a practical constraint for the next 100+ years of medical research.
The Conservative Default: Linear Assumption
Given genuine uncertainty about whether returns are diminishing or compounding, our analysis assumes a linear relationship between trial capacity and treatment discoveries. This is the conservative choice because:
- It’s the neutral prior: Without strong evidence for either diminishing or compounding returns, linearity is the least assumptive model
- It may underestimate benefits: If platform technologies and learning effects produce compounding returns, our projections are conservative
- It’s empirically defensible: The RECOVERY trial’s success (multiple treatments found with increased search) is consistent with linear or better returns
- It avoids both failure modes: Assuming diminishing returns would justify inaction; assuming compounding returns might overstate benefits. Linearity is the responsible middle ground
Bottom line: Even under the conservative linear assumption, 12.3x (95% CI: 4.19x-61.3x) more trials produces 12.3x (95% CI: 4.19x-61.3x) more discoveries from a space that is 99%+ unexplored. The expected value calculation remains overwhelmingly positive.
Sensitivity Analysis Approach
The analysis employs comprehensive sensitivity testing across multiple scenarios to assess robustness of findings:
Conservative Scenario (637:1 (95% CI: 569:1-790:1) ROI):
Optimistic Scenario (84.8M:1 (95% CI: 46.6M:1-144M:1) ROI):
Complete Case (84.8M:1 (95% CI: 46.6M:1-144M:1) ROI):
- Includes all eight quantifiable benefit categories
- Peace dividend: $114B (95% CI: $90.1B-$141B)
- Earlier treatment access, research acceleration, rare disease treatments, drug price reductions, prevention medicine, mental health benefits
Probabilistic sensitivity analysis: We ran 10,000 Monte Carlo simulations where each uncertain parameter was randomly sampled from probability distributions. The chart below shows the resulting ROI distributions with 95% confidence intervals.
What we varied: Cost reduction (50-95%), political success probability, adoption timeline (3-8 years), discount rate (1-7%), and QALY gains (0.7-1.3× baseline).
Economic interpretation: ROI > 1:1 means benefits exceed costs. All simulations produce ROI > 1:1, meaning there is effectively zero probability (within the modeled uncertainty) that this intervention loses money. Even the most conservative scenario (R&D savings only at 637:1 (95% CI: 569:1-790:1)) generates positive returns. This qualifies as a dominant intervention in health economics: it should be implemented regardless of budget constraints, as it generates net economic surplus while improving health outcomes.
Which parameters matter most for conservative ROI? The tornado chart below shows the sensitivity of the R&D-only ROI estimate to each input parameter. Parameters at the top have the largest impact on the final result:
For comprehensive sensitivity analysis including tornado charts for all calculated parameters, see Parameters and Calculations.
Key Analytical Assumptions
This analysis rests on several core assumptions that should be made explicit for academic transparency:
Strategic Stability Assumption
Assumption: A coordinated 1% reduction in military spending across all nations maintains relative power balances and strategic deterrence capabilities.
Justification: The 1% Treaty explicitly requires proportional reductions from all signatories. Since relative military capabilities remain unchanged, strategic stability is preserved. Historical analysis shows that symmetric reductions in military tensions (e.g., START treaties, naval treaties between world wars) maintained deterrence while reducing absolute expenditure.
Sensitivity: This assumption is critical to the peace dividend calculation. Alternative scenarios modeling unilateral reductions would require different political economy frameworks.
Linear Scaling Assumption
Assumption: Economic benefits and costs scale approximately linearly with program scope and adoption rates.
Justification: Conservative assumption that costs scale with system usage. Research acceleration benefits may exhibit superlinear returns (network effects, data abundance), making this assumption conservative.
Adoption Rate Assumptions
Assumption: The framework achieves gradual adoption following a 5 years linear ramp to 50%-80% participation rate among eligible trials.
Conservative case: 50% of trials adopt the pragmatic trial methodology Optimistic case: 80% adoption rate
Justification: Based on historical adoption curves for electronic health records (5-10 years to majority adoption), clinical trial registry systems, and FDA Sentinel System implementation.
Adoption realism considerations: Technology adoption typically follows S-curve dynamics with critical mass thresholds rather than linear ramps. Coordination failure risk exists (prisoner’s dilemma: pharmaceutical companies may prefer others adopt first). Mitigation: Economic incentives (82x (95% CI: 50x-94.1x) cost reduction) create overwhelming financial motivation for early adoption. Regulatory harmonization across jurisdictions may extend to 10-20 years rather than the modeled 5-year timeline, though pilot programs in willing jurisdictions (UK MHRA, which accepted RECOVERY evidence) can establish proof-of-concept earlier.
Sensitivity: NPV calculations explicitly model adoption uncertainty through gradual ramp-up rather than immediate full adoption. Conservative scenario (50% adoption) accounts for coordination failures and regulatory delays.
Cost Reduction Assumptions
Assumption: The methodology of a decentralized FDA reduces per-patient trial costs by 97.7% (95% CI: 97.5%-98.9%) (conservative) to 95% (optimistic) compared to traditional randomized controlled trials.
Historical Precedent: Pre-1962 Physician-Led Efficacy Trials
Context: A decentralized FDA approach is not an untested innovation extrapolated from a single case study. The Harvard meta-analysis of 108 embedded pragmatic trials132 demonstrates that cost reductions are reproducible across therapeutic areas, not unique to RECOVERY’s COVID emergency conditions. Moreover, this approach represents a return to the physician-led, real-world evidence model that operated successfully from 1883 to 1960 before being replaced by the current centralized system.
Cost structure comparison demonstrates dramatic efficiency difference:
- Pre-1962 system: $24.7M (95% CI: $19.5M-$30M)80 per drug (2024 inflation-adjusted) for safety testing; efficacy determined through decentralized physician case reports
- Post-1962 system: $2.60B (95% CI: $1.50B-$4B) per drug average, a 105x (95% CI: 90.6x-119x) cost increase; drug companies conduct both safety and efficacy trials internally
- Pragmatic trial model: Return to decentralized physician-led efficacy testing with modern automation (electronic health records, AI-assisted analysis, real-time data aggregation), targeting 50-95% cost reductions
The cost explosion began exactly when efficacy testing was centralized within pharmaceutical companies. This wasn’t a natural evolution of drug development or increasing drug complexity. It was a regulatory mandate that increased costs 105x (95% CI: 90.6x-119x)-fold while slowing innovation.
The regulatory causation is clear: The same types of compounds (small molecules, biologics) that cost $24.7M (95% CI: $19.5M-$30M) to develop in 1960 now cost $2.60B (95% CI: $1.50B-$4B). The molecules didn’t get more complex; the regulatory requirements did. Aspirin, if discovered today under current regulations, would cost billions to approve despite being chemically identical to the version approved for pennies in the pre-1962 era.
Historical operational model
From 1883 to 1960, 144 thousand physicians across America tested drug efficacy on real patients in routine clinical practice. The Journal of the American Medical Association (JAMA)147 compiled these observational reports, leading medical experts peer-reviewed the aggregated data, and effective treatments received endorsement.
Safety record, the thalidomide success story: The pre-1962 safety testing framework successfully prevented the thalidomide disaster148 that devastated Europe with thousands of horrific birth defects149. When thalidomide was marketed in Europe starting in 1957 for morning sickness, existing FDA safety regulations (1938 Food, Drug, and Cosmetic Act) blocked the drug from approval in the United States. Zero American babies were harmed - the safety testing framework worked exactly as intended.
The 1962 Kefauver-Harris Amendment added extensive efficacy requirements in response to thalidomide, despite the fact that the US had already been fully protected by existing safety regulations. The problem was not insufficient regulation; safety testing had succeeded. The response was to take efficacy testing away from 144 thousand physicians independent physicians and centralize it within pharmaceutical companies, increasing costs 105x (95% CI: 90.6x-119x)-fold while slowing approvals substantially.
Implications for generalizability
The RECOVERY trial ($500 (95% CI: $400-$2.50K)83 per patient) demonstrates that modern infrastructure enables even greater efficiency than the pre-1962 system. (Our system projections use $929 (95% CI: $97-$3K)/patient based on the ADAPTABLE trial.) However, the fundamental approach, physicians testing treatments on real patients in clinical practice settings, has 77 years of empirical validation (1883-1960), not merely one case study.
The cost reduction estimates are conservative relative to historical costs. 1980s drugs cost approximately $194M (95% CI: $146M-$242M) (compounded, 1990 dollars)20 compared to modern $2.60B (95% CI: $1.50B-$4B) costs20, representing a 13.4x (95% CI: 11.9x-14.7x)-fold increase. Modern technology (EHRs, wearables, automated data collection) suggests efficiency gains could exceed historical precedent while maintaining the safety protections that successfully prevented disasters like thalidomide.
Political Feasibility Assumption
Assumption: The 1% Treaty achieves ratification by sufficient nations within a 3-5 year campaign timeline.
Justification: Historical treaty adoption timelines vary (Nuclear Non-Proliferation Treaty: 3 years; Paris Climate Agreement: 5 years). This analysis focuses on economic value conditional on implementation, not probability of political success.
Important caveat: This analysis does not model the probability distribution over political outcomes. The economic case (637:1 (95% CI: 569:1-790:1) to 84.8M:1 (95% CI: 46.6M:1-144M:1) ROI) holds if implemented, but political economy barriers to implementation are substantial and outside the scope of this cost-benefit analysis.
Expected Value Analysis Accounting for Political Risk
Standard economic practice: Cost-benefit analysis for interventions with implementation uncertainty requires expected value calculation:
\[E[ROI] = ROI_{conditional} \times P_{success}\]
The preceding analysis presents conditional benefits (returns IF implementation succeeds). Expected value analysis incorporates the probability of achieving political ratification and sustained commitment.
Political success probability: We model political success as uncertain (1% (95% CI: 0.1%-10%)) reflecting geopolitical uncertainty. The distribution below shows the assumed probability range:
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
Risk-adjusted expected ROI: 848k:1 (95% CI: 58.0k:1-4.76M:1)
\[
\begin{gathered}
E[ROI_{max}] \\
= ROI_{max} \times P_{success} \\
= 84.8M \times 1\% \\
= 848{,}000
\end{gathered}
\] where: \[
\begin{gathered}
ROI_{max} \\
= \frac{Value_{max}}{Cost_{campaign}} \\
= \frac{\$84800T}{\$1B} \\
= 84.8M
\end{gathered}
\] where: \[
\begin{gathered}
Value_{max} \\
= DALYs_{max} \times Value_{QALY} \\
= 565B \times \$150K \\
= \$84800T
\end{gathered}
\] where: \[
\begin{gathered}
DALYs_{max} \\
= DALYs_{global,ann} \times Pct_{avoid,DALY} \times T_{accel,max} \\
= 2.88B \times 92.6\% \times 212 \\
= 565B
\end{gathered}
\] where: \[
T_{accel,max} = T_{accel} + T_{lag} = 204 + 8.2 = 212
\] where: \[
\begin{gathered}
T_{accel} \\
= T_{first,SQ} \times \left(1 - \frac{1}{k_{capacity}}\right) \\
= 222 \times \left(1 - \frac{1}{12.3}\right) \\
= 204
\end{gathered}
\] where: \[
\begin{gathered}
T_{first,SQ} \\
= T_{queue,SQ} \times 0.5 \\
= 443 \times 0.5 \\
= 222
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{campaign} \\
= Budget_{viral,base} + Budget_{lobby,treaty} \\
+ Budget_{reserve} \\
= \$250M + \$650M + \$100M \\
= \$1B
\end{gathered}
\]
The tornado chart below shows how expected ROI varies with political success probability - this is the primary driver of uncertainty:
The Monte Carlo distribution shows the full range of expected ROI outcomes when sampling political success probability from its uncertainty distribution:
Simulation Results Summary: Expected Treaty ROI (Risk-Adjusted)
| Baseline (deterministic) |
848k:1 |
| Mean (expected value) |
962k:1 |
| Median (50th percentile) |
154k:1 |
| Standard Deviation |
1.80M:1 |
| 90% Range (5th-95th percentile) |
[58.0k:1, 4.76M:1] |
The histogram shows the distribution of Expected Treaty ROI (Risk-Adjusted) across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Comparison to traditional interventions (assuming 100% implementation probability):
Interpretation: The high conditional ROI (84.8M:1 (95% CI: 46.6M:1-144M:1)) means that even modest implementation probabilities yield expected values competitive with best-in-class health interventions that have near-certain implementation.
Note: The uncertainty analysis samples political probability from its full distribution (1% (95% CI: 0.1%-10%)). Actual probability depends on campaign execution, geopolitical conditions, and public support mobilization. The campaign strategy allocates $1B over 4 years specifically to maximize ratification probability.
Time Inconsistency and Commitment Credibility
Political economy challenge: Even if the treaty achieves initial ratification, sustained commitment over the 10 years analytical horizon faces time inconsistency problems. Political business cycles (2-6 year terms) create incentives to raid the pragmatic clinical trials budget for short-term priorities.
The Iron Triangle problem: Military contractors have concentrated interests with substantial lobbying capacity ($127M17 annually), creating tight coordination between defense industry, congressional committees, and Pentagon bureaucracy. Health benefits, while larger in aggregate ($172B (95% CI: $140B-$213B) annually), are diffuse across millions of beneficiaries who lack equivalent lobbying infrastructure. This asymmetry (concentrated producer benefits vs. diffuse consumer benefits) creates political economy barriers to reallocation even when aggregate welfare gains are enormous.
The billionaire mortality paradox: This diffusion argument has a critical exception. The world’s ~3,000 billionaires (with combined wealth exceeding $14 trillion) are themselves patients who will die of cancer, heart disease, or aging. Unlike defense contractors who profit regardless of personal health outcomes, billionaires have concentrated personal stakes in medical progress: their own mortality and that of everyone they love. A single billionaire spending $1B on treaty advocacy has ~1% (95% CI: 0.1%-10%) probability of unlocking $27.2B/year in government funding. The personal benefit (years of additional life expectancy, treatments for diseases that would otherwise kill them and their families) is worth far more than $1B to someone with $100B+ who cannot currently buy immortality or treatments that don’t exist. The puzzle isn’t that benefits are truly diffuse. Billionaires face the same mortality as everyone else, and their wealth becomes worthless when they’re dead. The puzzle is why structural barriers (prestige bias toward labs over lobbying, political risk aversion, bad advice from scientists saying “fund my lab” rather than “hire lobbyists”) prevent them from acting on their concentrated personal interest in not dying.
Historical precedent: Why past peace dividends failed: The post-World War II “peace dividend” saw military spending fall from 41% of GDP (1945) to 7.2% (1948)79, with expectations of permanent reductions. However, the Cold War reversed this within 3 years. Military spending returned to 15% of GDP by 1953. Similar patterns occurred post-Vietnam (1970s) and post-Cold War (1990s): initial reductions followed by reversals within 5-10 years. The critical failure: savings weren’t bound to a substitute industry. Money reverted to general budgets, making re-militarization politically costless. The 1% Treaty solves this by contractually binding savings to health research infrastructure, creating a new constituency (patients, researchers, pharmaceutical companies) with incentives to defend the reallocation.
Treaty ratification ≠ sustained funding: The Paris Climate Agreement provides a cautionary example: 196 parties ratified, but many failed to meet funding commitments. As of 2024, developed countries have not met the $100B annual climate finance pledge despite treaty obligations. Treaty ratification creates moral commitment but weak enforcement mechanisms for sustained budgetary allocations.
Implication for expected value: The political success probabilities used in expected value analysis (1% (95% CI: 0.1%-10%)) implicitly incorporate time inconsistency risk. The expected value analysis partially addresses this through probability discounting, but time inconsistency (commitment erosion over time) represents an additional risk factor beyond initial political feasibility.
Potential commitment mechanisms (not modeled):
- Constitutional amendment (very high barrier, very high credibility)
- Independent funding agency with statutory protections
- Lock-box mechanism with supermajority requirement to redirect funds
- International monitoring and reputation costs
- Public transparency: all spending and trial outcomes publicly auditable
Note: The analysis acknowledges this limitation. Results should be interpreted as conditional on sustained implementation, with expected value analysis providing probability-adjusted estimates that partially account for political risk.
Technology Constancy Assumption
Assumption: Analysis does not incorporate potential advances in AI, automation, or biotechnology that could further accelerate research.
Justification: Conservative assumption. Emerging AI capabilities in drug discovery, automated synthesis, and computational biology could dramatically increase research productivity beyond modeled estimates.
Implication: Baseline estimates likely underestimate long-term benefits by excluding technology-driven accelerations.
Data Quality and Availability
All primary data sources are documented in References with confidence levels:
- High confidence (78%): SIPRI military expenditure, WHO mortality statistics, ClinicalTrials.gov data
- Medium confidence (17%): Peace dividend estimates, QALY valuations (wide range in literature)
- Conservative bounds: Where uncertainty exists, analysis uses conservative estimates favoring underestimation of benefits
For complete parameter documentation with confidence indicators and peer-review status, see Parameters and Calculations Reference.
Scenario Analysis: Complete Case
84.8M:1 (95% CI: 46.6M:1-144M:1) ROI
The conservative scenario counted only R&D efficiency gains. This section includes all quantifiable benefit categories.
Timeline Shift Value
The recurring benefits ($172B (95% CI: $140B-$213B)/year) are trivial compared to the timeline shift: $84.8 quadrillion (95% CI: $62.4 quadrillion-$97.3 quadrillion) from treatments arriving ~212 years (95% CI: 135 years-355 years) earlier on average.
Important Note: The system provides an average ~212 years (95% CI: 135 years-355 years) timeline shift (treatment discovery acceleration + efficacy lag elimination) in when diseases receive first effective treatments, not an annual recurring benefit. This timeline shift benefit is massive ($84.8 quadrillion (95% CI: $62.4 quadrillion-$97.3 quadrillion) total economic value) but represents an average acceleration in when treatments become available, not an annual stream. The recurring annual benefits above ($172B (95% CI: $140B-$213B)/year) represent only the peace dividend and R&D savings, which continue perpetually. See Regulatory Mortality Analysis for timeline shift methodology.
Complete Case ROI
\[
\begin{gathered}
ROI_{max} \\
= \frac{Value_{max}}{Cost_{campaign}} \\
= \frac{\$84800T}{\$1B} \\
= 84.8M
\end{gathered}
\] where: \[
\begin{gathered}
Value_{max} \\
= DALYs_{max} \times Value_{QALY} \\
= 565B \times \$150K \\
= \$84800T
\end{gathered}
\] where: \[
\begin{gathered}
DALYs_{max} \\
= DALYs_{global,ann} \times Pct_{avoid,DALY} \times T_{accel,max} \\
= 2.88B \times 92.6\% \times 212 \\
= 565B
\end{gathered}
\] where: \[
T_{accel,max} = T_{accel} + T_{lag} = 204 + 8.2 = 212
\] where: \[
\begin{gathered}
T_{accel} \\
= T_{first,SQ} \times \left(1 - \frac{1}{k_{capacity}}\right) \\
= 222 \times \left(1 - \frac{1}{12.3}\right) \\
= 204
\end{gathered}
\] where: \[
\begin{gathered}
T_{first,SQ} \\
= T_{queue,SQ} \times 0.5 \\
= 443 \times 0.5 \\
= 222
\end{gathered}
\] where: \[
\begin{gathered}
T_{queue,SQ} \\
= \frac{N_{untreated}}{Treatments_{new,ann}} \\
= \frac{6{,}650}{15} \\
= 443
\end{gathered}
\] where: \[
\begin{gathered}
N_{untreated} \\
= N_{rare} \times 0.95 \\
= 7{,}000 \times 0.95 \\
= 6{,}650
\end{gathered}
\] where: \[
\begin{gathered}
k_{capacity} \\
= \frac{N_{fundable,ann}}{Slots_{curr}} \\
= \frac{23.4M}{1.9M} \\
= 12.3
\end{gathered}
\] where: \[
\begin{gathered}
N_{fundable,ann} \\
= \frac{Subsidies_{trial,ann}}{Cost_{pragmatic,pt}} \\
= \frac{\$21.7B}{\$929} \\
= 23.4M
\end{gathered}
\] where: \[
\begin{gathered}
Subsidies_{trial,ann} \\
= Treasury_{RD,ann} - OPEX_{dFDA} \\
= \$21.8B - \$40M \\
= \$21.7B
\end{gathered}
\] where: \[
\begin{gathered}
OPEX_{dFDA} \\
= Cost_{platform} + Cost_{staff} + Cost_{infra} \\
+ Cost_{regulatory} + Cost_{community} \\
= \$15M + \$10M + \$8M + \$5M + \$2M \\
= \$40M
\end{gathered}
\] where: \[
\begin{gathered}
Treasury_{RD,ann} \\
= Funding_{treaty} - Payout_{bond,ann} - Funding_{political,ann} \\
= \$27.2B - \$2.72B - \$2.72B \\
= \$21.8B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{treaty} \\
= Spending_{mil} \times Reduce_{treaty} \\
= \$2.72T \times 1\% \\
= \$27.2B
\end{gathered}
\] where: \[
\begin{gathered}
Payout_{bond,ann} \\
= Funding_{treaty} \times Pct_{bond} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Funding_{political,ann} \\
= Funding_{treaty} \times Pct_{political} \\
= \$27.2B \times 10\% \\
= \$2.72B
\end{gathered}
\] where: \[
\begin{gathered}
Cost_{campaign} \\
= Budget_{viral,base} + Budget_{lobby,treaty} \\
+ Budget_{reserve} \\
= \$250M + \$650M + \$100M \\
= \$1B
\end{gathered}
\]
Translation: Every $1 invested returns $84.8M:1 (95% CI: 46.6M:1-144M:1) in recurring annual benefits (peace dividend + R&D savings), plus a ~212 years (95% CI: 135 years-355 years) average timeline shift in disease eradication (not included in annual figure).
Sensitivity of complete ROI: The tornado chart below shows which parameters most affect the complete ROI estimate:
These estimates derive from:
- Proven trial costs (RECOVERY: 82x (95% CI: 50x-94.1x) cost reduction demonstrated)
- Disease prevalence data (WHO Global Health Observatory)
- Standard QALY valuations (health economics consensus thresholds)
Critical distinction - the two benefit categories are different things:
Investment required: $1B (one-time implementation cost)
Efficacy lag uncertainty: The timeline shift depends on the efficacy lag parameter, which represents years of regulatory delay after safety is established. The distribution below shows the uncertainty range:
This chart shows the assumed probability distribution for this parameter. The shaded region represents the 95% confidence interval where we expect the true value to fall.
Individual-Level Economic Impact
The aggregate societal benefits ($172B (95% CI: $140B-$213B)-$172B (95% CI: $140B-$213B) annually) result from individual economic gains multiplied across billions of people. Understanding individual impact helps explain both the scale and the equity of the Disease Eradication Model.
Simulation Results Summary: Personal Lifetime Wealth (QALY-Based)
| Baseline (deterministic) |
$3M |
| Mean (expected value) |
$3.41M |
| Median (50th percentile) |
$1.88M |
| Standard Deviation |
$4.41M |
| 90% Range (5th-95th percentile) |
[$259K, $12.1M] |
The histogram shows the distribution of Personal Lifetime Wealth (QALY-Based) across 10,000 Monte Carlo simulations. The CDF (right) shows the probability of the outcome exceeding any given value, which is useful for risk assessment.
Who Benefits and How
The 1% Treaty creates positive economic incentives across all major groups, eliminating traditional opposition to healthcare system reform. This alignment makes it politically feasible and sustainable.
Who Gets What (see Aligning Incentives for details):
- Military sector: Keeps 99% of current budget
- Pharmaceutical industry: Trial costs shift from expense to revenue (patients fund participation); research capacity increases 12.3x (95% CI: 4.19x-61.3x)
- Insurance companies: Net savings from reduced disease burden43 ($109T (95% CI: $79.8T-$144T) current economic cost)
- Healthcare providers: More treatment options; earlier access to effective therapies
- Patients: Access to clinical trials as healthcare and new treatments years or decades sooner
- Taxpayers: Net reduction in taxes and healthcare costs through improved R&D efficiency
See Aligning Incentives for detailed analysis and implementation strategy.
Adoption Dynamics: Game-Theoretic Analysis
Western economies are facing a solvency crisis driven by healthcare inflation and aging populations. Traditional approaches face severe constraints: austerity programs cutting benefits generate political backlash, while monetary expansion through Modern Monetary Theory risks inflation. Technological deflation through dramatically reduced clinical trial costs offers an alternative path.
By collapsing the cost of clinical trials by 44.1x (95% CI: 39.4x-89.1x), we fundamentally alter the cost structure of healthcare. We replace expensive “chronic disease management” with cheap “curative interventions.” This is the only mathematically viable path to long-term fiscal solvency for G7 nations. It is impossible not to fund this, because the alternative is national bankruptcy.
Implementation Strategy
The economic benefits outlined above demonstrate the value proposition of the 1% Treaty system. Implementation requires political mobilization to achieve treaty adoption:
Step 1: Global Mandate (The Philanthropic Catalyst)
Goal: Survey 3.5% of the global population (280 million of people).
Why 3.5%?: Historical analysis (Chenoweth et al.) shows that no government has withstood nonviolent civil challenge from 3.5% of its population. This “Shadow Mandate” would increase political pressure for treaty ratification.
Funding: This educational and scientific polling initiative is the primary entry point for philanthropic partners, validating global demand before the main campaign begins.
Step 2: Capitalization via Incentive Alignment Bonds (IABs)
A Special Purpose Vehicle (SPV) issues Incentive Alignment Bonds to capitalize the advocacy roadmap. By front-loading the cost of political change, investors capture the arbitrage gap between lobbying costs ($1B) and sovereign flows ($27.2B/year). Financial modeling projects a risk-adjusted IRR of ~272%.
Step 3: Implement the Legislative Strategy
Deploy Incentive Alignment Bond proceeds to translate public support into legislative action.
Step 4: Build the Infrastructure
The 1% shift funds globally scaled pragmatic trial infrastructure modeled on RECOVERY’s approach. Thousands of neglected treatments finally get tested. Effective ones scale instantly.
Technical requirements: Building this requires EHR interoperability, data standards, automated analysis pipelines, and regulatory framework updates. RECOVERY demonstrated the core model works; scaling requires infrastructure investment but no fundamental technical breakthroughs. The challenge is deployment and adoption, not invention.
Step 5: The Statutory Administration Utility
The Treaty mandates that the Fund be managed by a private Central Counterparty to ensure operational efficiency and accountability.
The mechanism:
- 12.3x (95% CI: 4.19x-61.3x) more trial capacity to test treatments simultaneously
- Disease categories collapse as effective treatments scale
- Healthspan overtakes pathology
The utility structure: The SPV retains a perpetual 10% Statutory Administration Fee on all inflows ($2.72B/year projected) to cover vetting, auditing, and operations. This converts the IAB from a debt instrument into a perpetual equity claim on the Global Health Budget.
Governance constraints (addressing self-dealing concerns):
- Independent board: Majority of seats held by treaty signatory representatives, not SPV founders
- Capped compensation: Administrator salaries benchmarked to comparable multilateral institutions (WHO, World Bank)
- Annual third-party audit: Published financials with signatory oversight committee review
- Sunset provision: Fee percentage subject to 10-year renegotiation by signatory majority
- Operational scope: Fee funds only treaty defense lobbying, compliance monitoring, and fund administration (not founder enrichment)
Utility shareholders (bondholders) receive dividends from the Administration Fee, creating a permanent constituency to defend the Treaty against political cuts. We do not rely on altruism. We rely on the “Iron Dome” effect: The Administration Fee creates a well-funded lobby whose only job is to protect the Treaty’s existence.
Implementation complexity: Coordinating global treaty adoption, building technical infrastructure, and integrating with existing health systems presents significant logistical challenges. However, these are coordination problems with aligned incentives, not conflicts of interest. Similar to how nations coordinated on the Montreal Protocol (ozone layer) or the International Space Station despite complexity, the economic case makes cooperation rational even for self-interested actors.
For comprehensive implementation details, see Incentive Alignment Bonds for the proposed financing mechanism.
Implementation Budget Breakdown
The $1B implementation cost (used as denominator in complete case 84.8M:1 (95% CI: 46.6M:1-144M:1) ROI) allocates funds across three strategic categories:
| Global Referendum |
$250M |
Global direct democracy campaign (280 million of people votes). Creates a “Shadow Mandate” and political cost for non-adoption. Not legally binding, but politically coercive. |
| Legislative Advocacy |
$650M |
Legislative outreach (US/EU/G20), policy education, military industry conversion, legal/compliance, opposition research. Outspends pharma + MIC combined |
| Reserve Fund |
$100M |
Post-victory transition, treaty implementation support, contingency buffer |
| Total Implementation Cost |
$1B |
4-year implementation timeline |
\[
\begin{gathered}
Cost_{campaign} \\
= Budget_{viral,base} + Budget_{lobby,treaty} \\
+ Budget_{reserve} \\
= \$250M + \$650M + \$100M \\
= \$1B
\end{gathered}
\]
Philanthropic Leverage: For a philanthropic partner, the leverage works in two phases:
- Phase 1 (The Catalyst): A $250M grant for the Global Survey provides the proof-of-demand that de-risks the private capital raise, unlocking the $1B bond market
- Phase 2 (Policy Change): That $1B campaign convinces governments to redirect $27.2B/year from military to pragmatic clinical trials
Total Leverage: The $250M philanthropic catalyst + $650M campaign investment unlocks $27.2B/year in redirected government spending.
Why such high leverage is achievable: This isn’t a traditional financial return. It’s policy leverage. Philanthropic capital funds advocacy that shifts existing government budgets. Similar mechanisms:
- Gates Foundation’s $10B vaccine pledge leveraged $200B+ in government commitments (20x policy leverage)
- Climate advocacy: $50M campaigns regularly shift billions in energy policy
- Tobacco control: Bloomberg’s $1B unlocked $15B+ in government tobacco control spending (15x leverage)
The 1% Treaty targets a much larger budget reallocation (1% of $11.4T (95% CI: $9.01T-$14.1T) global military spending), making the leverage ratio proportionally higher. The key difference: military budgets are ~1000x larger than typical philanthropic targets, enabling proportionally higher leverage when successfully redirected.
This budget is designed for a 3-5 year campaign to achieve treaty ratification by major powers, representing less than 4% of the first year’s conservative benefits ($172B (95% CI: $140B-$213B)). The referendum component isn’t a “magic wand”; it’s a mechanism to generate the political capital required to force the treaty onto the agenda of sovereign nations.
This economic analysis focuses on the return on investment once the framework is operational, demonstrating that the intervention generates 637:1 (95% CI: 569:1-790:1) to 84.8M:1 (95% CI: 46.6M:1-144M:1) returns regardless of the specific path to adoption.
Detailed Technical References
For the rigorous analysis:
Risk Analysis and Mitigation
This section addresses common objections and potential failure modes, along with specific mitigation strategies.
The “But Politicians Won’t Do It” Problem
What could go wrong: Politicians refuse to redirect 1% of military spending to pragmatic clinical trials because military contractors oppose the change.
Counterargument:
Military lobbyists currently get $1,813 back for every $1 spent150 on political influence. The proposed model offers Incentive Alignment Bond holders ~272% in perpetuity (allocating 10% of the $27.2B annual inflows to bond payouts).
This creates a financial “kill switch”: if the treaty is not respected, this massive income stream stops. This aligns the most powerful interests on earth with treaty compliance.
Budgetary Reality: The Pentagon has failed its sixth consecutive audit and cannot account for $2.5 trillion in assets. A 1% reduction is statistical noise in a system that can’t locate trillions. It doesn’t require firing people or closing factories; it requires accounting for rounding errors.
This doesn’t defeat greed. It aligns economic incentives to direct existing profit motives toward pragmatic clinical trials.
Historical precedent: After WW2, military spending was cut by 30%79, contributing to substantial economic growth. The proposed 1% reduction is significantly more modest.
Safety Concerns
Objection: Pragmatic trials with lower costs may compromise safety by missing dangerous side effects.
Response: The empirical evidence indicates the opposite. The proposed system provides superior safety monitoring compared to traditional trials across multiple dimensions: sample size, population diversity, monitoring duration, publication completeness, and adverse event detection speed.
Current system limitations:
- Voluntary adverse event reporting captures an estimated 1-10% of actual events (FDA assessment)
- Traditional Phase III trials test 100-300 patients for 3-12 months, then monitoring stops
- Approximately 50% of trial results go unpublished, with publication bias favoring positive findings 3:1
- 86.1% of patients excluded from trials due to age, comorbidities, or concurrent medications, meaning safety signals in these populations remain undetected
- Long-term effects (>1 year) are rarely captured in pre-approval trials
Proposed system safety advantages:
Mandatory universal data collection: The system automatically collects and publishes outcome data on all treatments and all health outcomes using existing EHR infrastructure. This is not currently done systematically for approved drugs.
Continuous population-scale monitoring: Pragmatic trials with 10,000-100,000+ participants monitored continuously through EHR integration detect safety problems faster and more reliably than small, time-limited traditional trials. The RECOVERY trial identified both effective treatments (dexamethasone) and harmful ones (hydroxychloroquine) in under 100 days with 47,000 patients - faster and more definitively than traditional trial timelines.
Preserved Phase I safety testing: The proposal retains rigorous Phase I safety testing (~2.3 years), which successfully prevented the thalidomide disaster in the United States. What changes is eliminating the 8.2 years (95% CI: 4.85 years-11.5 years) efficacy delay after safety is verified. Phase I safety assessment remains mandatory.
Ubiquitous adverse event detection: The Vioxx cardiovascular risk135 took 5 years to detect through voluntary reporting and dedicated post-market studies (1999-2004), resulting in 38,000-55,000 estimated deaths135. Automated EHR monitoring comparing cardiovascular event rates in treated patients versus matched controls would have detected the elevated risk within 6-12 months. The proposed system implements ubiquitous automated monitoring from day one, not years later.
Immediate mass notification: When safety signals are detected, all patients currently taking the drug receive automated alerts through patient portals, enabling immediate clinical review and discontinuation if warranted. Current voluntary reporting systems lack this capability.
Comparative safety surveillance:
| Sample size |
100-300 patients |
10,000-100,000+ patients |
| Patient selection |
86.1% excluded (comorbidities, age, medications) |
All volunteers included (real-world populations) |
| Monitoring duration |
3-12 months (then stops) |
Continuous through EHR integration (indefinite) |
| Publication rate |
~50% unpublished133; positive results 3× more likely published |
100% automatically published (automated data aggregation) |
| Subpopulation safety |
Excludes elderly, children, pregnant patients |
Tests all populations, detects subpopulation-specific risks |
| Long-term effects |
Rarely captured (<1 year observation) |
Continuous multi-year tracking via EHR linkage |
| Adverse event detection |
Voluntary physician reporting (1-10% capture rate) |
Automated statistical surveillance (100% capture of recorded events) |
| Mass notification |
Manual, slow, incomplete |
Automated, immediate, comprehensive |
| Comparative effectiveness |
Single treatment vs. placebo (or one comparator) |
Multiple treatments randomized simultaneously; enables ranking |
| Population stratification |
Not possible (86.1% excluded; narrow population) |
Full subgroup analysis by demographics, genetics, comorbidities |
Type II error dominance: Regulatory mortality analysis quantifies the harm ratio at 3.07k:1 (95% CI: 2.88k:1-3.12k:1). For every person protected from an unsafe drug approval (Type I error prevention), 3.07k:1 (95% CI: 2.88k:1-3.12k:1) people die from delayed access to beneficial treatments (Type II errors). The current regulatory framework successfully prevents toxic compounds from reaching patients through Phase I safety testing - as demonstrated by thalidomide’s prevention in the United States - but the barriers placed between patients and beneficial treatments after safety verification cause 3.07k:1 (95% CI: 2.88k:1-3.12k:1) more deaths than they prevent.
\[
\begin{gathered}
Ratio_{TypeII} \\
= \frac{DALYs_{lag}}{DALY_{TypeI}} \\
= \frac{7.94B}{2.59M} \\
= 3{,}070
\end{gathered}
\] where: \[
DALYs_{lag} = YLL_{lag} + YLD_{lag} = 7.07B + 873M = 7.94B
\] where: \[
\begin{gathered}
YLL_{lag} \\
= Deaths_{lag} \times (LE_{global} - Age_{death,delay}) \\
= 416M \times (79 - 62) \\
= 7.07B
\end{gathered}
\] where: \[
\begin{gathered}
Deaths_{lag} \\
= T_{lag} \times Deaths_{disease,daily} \times 338 \\
= 8.2 \times 150{,}000 \times 338 \\
= 416M
\end{gathered}
\] where: \[
\begin{gathered}
YLD_{lag} \\
= Deaths_{lag} \times T_{suffering} \times DW_{chronic} \\
= 416M \times 6 \times 0.35 \\
= 873M
\end{gathered}
\] where: \[
\begin{gathered}
DALY_{TypeI} \\
= DALY_{thal} \times 62 \\
= 41{,}800 \times 62 \\
= 2.59M
\end{gathered}
\] where: \[
\begin{gathered}
DALY_{thal} \\
= YLD_{thal} + YLL_{thal} \\
= 13{,}000 + 28{,}800 \\
= 41{,}800
\end{gathered}
\] where: \[
\begin{gathered}
YLD_{thal} \\
= DW_{thal} \times N_{thal,survive} \times LE_{thal} \\
= 0.4 \times 540 \times 60 \\
= 13{,}000
\end{gathered}
\] where: \[
\begin{gathered}
N_{thal,survive} \\
= N_{thal,US,prevent} \times (1 - Rate_{thal,mort}) \\
= 900 \times (1 - 40\%) \\
= 540
\end{gathered}
\] where: \[
\begin{gathered}
N_{thal,US,prevent} \\
= N_{thal,global} \times Pct_{US,1960} \\
= 15{,}000 \times 6\% \\
= 900
\end{gathered}
\] where: \[
\begin{gathered}
YLL_{thal} \\
= Deaths_{thal} \times 80 \\
= 360 \times 80 \\
= 28{,}800
\end{gathered}
\] where: \[
\begin{gathered}
Deaths_{thal} \\
= Rate_{thal,mort} \times N_{thal,US,prevent} \\
= 40\% \times 900 \\
= 360
\end{gathered}
\]
Quantified mortality from efficacy delay: The 8.2 years (95% CI: 4.85 years-11.5 years) delay between Phase I safety verification and final approval has resulted in an estimated 416 million deaths (95% CI: 225 million deaths-630 million deaths) from 1962-2024 by delaying patient access to beneficial treatments that had already passed safety testing. This figure represents the cumulative mortality from requiring patients to wait ~8 years for efficacy confirmation after treatments are confirmed non-toxic, when those patients could have voluntarily participated in efficacy trials immediately following Phase I completion.
\[
\begin{gathered}
Deaths_{lag} \\
= T_{lag} \times Deaths_{disease,daily} \times 338 \\
= 8.2 \times 150{,}000 \times 338 \\
= 416M
\end{gathered}
\]
Cost reduction does not imply quality reduction: The 82x (95% CI: 50x-94.1x) cost reduction achieved by the RECOVERY trial came from eliminating duplicative infrastructure (using existing hospitals instead of building dedicated trial sites, using existing EHR data instead of parallel data collection systems), not from reducing sample sizes, shortening observation periods, or relaxing safety standards. Lower cost reflects infrastructure efficiency, not reduced scientific rigor.
For detailed mortality analysis, see Regulatory Mortality Analysis.
Patient Agency and Autonomy
A decentralized institutes of health puts patients in control through trial participation, not committee votes.
Current system: 200 NIH bureaucrats151 decide what 8.00 billion of people (95% CI: 7.80 billion of people-8.20 billion of people) humans can try when dying
New system: Patients choose which trials to join. Trials that attract patients get funded. Trials that don’t, die.
Patient subsidies follow them to whichever trial they join. Researchers compete to design trials that patients actually want to participate in. No committees, no grant-writing contests, no bureaucrats deciding what’s “worthy” of study.
All transactions publicly recorded. All spending transparent. All decisions auditable.
Patients select which trials to join. Trials that attract participants receive funding. Researchers compete for patient participation rather than committee grants.
The system operates through distributed infrastructure:
- Open-source protocols (anyone can verify how it works)
- Distributed validation (no single point of failure)
- Works with existing regulators (additive layer, not replacement)
Accountability measures
- Annual third-party audits of 1% Treaty Fund and system operations
- Public reporting of all spending and outcomes
- Milestone-based funding (money releases when targets hit)
See Anti-Capture Design and Legal Architecture for accountability mechanisms designed to prevent administrative delays and ensure timely fund deployment.
Limitations and Uncertainties
This analysis acknowledges several important limitations and sources of uncertainty inherent in modeling a transformative policy intervention of this scale.
Adoption Timeline Uncertainty
The base case assumes gradual adoption over 5 years to full implementation. Actual adoption may be faster or slower depending on:
- Regulatory harmonization: International coordination requirements may extend implementation timelines
- Technical infrastructure readiness: EHR interoperability, data standardization, and privacy compliance vary significantly across jurisdictions
- Industry cooperation: Pharmaceutical companies, regulators, and healthcare providers will resist or accelerate adoption based on whether they profit from it
Sensitivity analysis addresses this: Worst-case scenario models extended timelines with ROI remaining positive (66:1) even under pessimistic assumptions.
Pragmatic Trial Internal Validity and Selection Bias
Decentralized trials with broad eligibility criteria face potential selection bias concerns. Traditional randomized controlled trials use restrictive eligibility precisely to control confounding and establish internal validity.
Trade-off between internal and external validity: Patsopoulos (2011)152 documents that pragmatic trials often find 15-25% smaller effect sizes than explanatory trials but offer superior external validity (generalizability to real-world populations).
Mitigation strategies
- Randomization preserved: The global pragmatic trial system maintains random treatment assignment (the core causal identification strategy)
- Large sample sizes: Decentralized recruitment enables 10-100× larger trials, improving statistical power and subgroup analysis
- Covariate adjustment: Electronic health record data enables controlling for confounders ex-post using propensity score matching and instrumental variables
- Replication at scale: Lower costs enable rapid replication across diverse populations, testing robustness
Empirical evidence, observational studies produce valid results: A meta-analysis in the New England Journal of Medicine153 compared effect sizes from high-quality observational studies to randomized controlled trials across multiple interventions. The findings demonstrate that well-designed observational studies produce results statistically indistinguishable from expensive RCTs.
These meta-analytic findings support the validity of pragmatic trial designs used in this system. Modern statistical methods, large sample sizes, and proper covariate adjustment enable observational and quasi-experimental designs to achieve causal inference comparable to traditional RCTs at a fraction of the cost.
Why pragmatic trial data is more valuable than RCT data for clinical decisions:
Traditional RCTs answer: “Is treatment A better than placebo?” Pragmatic trials answer: “How do ALL available treatments rank for patients like mine?”
This distinction is crucial for clinical decision-making. A physician facing a patient with rheumatoid arthritis has 15+ approved treatment options. Traditional evidence provides isolated A-vs-placebo studies; the physician cannot determine whether methotrexate or adalimumab is superior for their specific patient. Pragmatic trials, by randomly assigning patients across all options simultaneously and including diverse populations, generate the comparative rankings clinicians actually need.
Furthermore, RCTs’ restrictive eligibility criteria (excluding patients with comorbidities, elderly patients, patients on multiple medications) mean their results don’t generalize to real patients. A 73-year-old with diabetes and hypertension was excluded from the original trials; the physician is guessing how results might apply. Pragmatic trials include these patients, enabling stratified effectiveness rankings by actual patient characteristics.
Historical precedent: Pre-1962 physician-led system successfully identified effective treatments (antibiotics, vaccines, surgical techniques) despite lacking modern randomization, suggesting real-world evidence can establish causality when combined with peer review and replication.
Publication bias: Traditional trials face severe publication bias: only 37% of negative results are published compared to 94% of positive results133, leading to overestimation of treatment effectiveness and ~$100 billion annually wasted on repeating failed experiments154. A decentralized FDA addresses this by design: all trials are registered in the public database, all results (positive and negative) are automatically published through the transparent data infrastructure, and the open data architecture ensures no selective reporting. Unlike traditional systems where researchers choose what to publish, mandatory publication of all registered trials eliminates publication bias as a concern.
Conclusion: Internal validity concerns are acknowledged, but the combination of randomization, large samples, and replication capacity provides adequate causal inference even with broader eligibility criteria.
QALY Calculation Uncertainties
The 565 billion DALYs (95% CI: 361 billion DALYs-877 billion DALYs) estimate aggregates benefits from the average ~212 years (95% CI: 135 years-355 years) timeline shift across three benefit streams with varying levels of empirical support.
Addressing the “Quadrillion Dollar” Assumption: The total economic value of $84.8 quadrillion (95% CI: $62.4 quadrillion-$97.3 quadrillion) derives from the average ~212 years (95% CI: 135 years-355 years) timeline shift in disease eradication.
How the timeline shift is calculated:
Discovery acceleration (~204 years (95% CI: 123 years-350 years) on average): With 12.3x (95% CI: 4.19x-61.3x) trial capacity, treatments are discovered ~204 years (95% CI: 123 years-350 years) earlier on average. This is based on therapeutic space exploration: 6.65 thousand diseases (95% CI: 5.70 thousand diseases-8.24 thousand diseases) lack treatment, with ~9.50 million combinations drug-disease combinations untested. At current exploration rate (~15 diseases/year getting first treatments), systematically testing this space would take 443 years (95% CI: 324 years-712 years). With 12.3x (95% CI: 4.19x-61.3x) capacity, exploration completes in ~36 years (95% CI: 11.6 years-77.2 years). Average disease receives treatment halfway through exploration period, yielding ~204 years (95% CI: 123 years-350 years) acceleration.
Efficacy lag elimination (~8.2 years (95% CI: 4.85 years-11.5 years)): Once a treatment is discovered, it reaches patients immediately instead of waiting ~8.2 years (95% CI: 4.85 years-11.5 years) for post-safety regulatory approval.
Why this estimate is still conservative:
- It assumes a fixed far-future timeline: Even if full biological control takes 1,000 years, shifting that timeline forward by ~212 years (95% CI: 135 years-355 years) on average saves that many years’ worth of future lives. Given the trajectory of biotechnology, “eventual” control over biology is a matter of when, not if.
- It works with partial success: Even if we assume 90% of diseases remain biologically incurable (a massive discount), accelerating treatments for just the “easiest” 10% of the burden (e.g., cardiovascular disease, metabolic disorders) still yields enormous value. The ROI is positive even at 1/100th of the projected success rate.
- It uses average acceleration: Some diseases with existing-but-untested treatments would be discovered much sooner (approaching 0 years wait); diseases requiring novel mechanisms would take longer. The 204 years (95% CI: 123 years-350 years) figure is the average across the distribution.
Stream A (Accelerated Drug Access): High confidence, based on well-documented costs of delayed access (84,000 life-years lost per year delay in cancer therapies alone).
Stream B (Prevention via Real-World Evidence): Medium confidence, preventative care benefits are well-established, but scale of improvement from comprehensive data remains uncertain.
Stream C (Rare Disease Treatments): Lower confidence, economic viability of rare disease research is theoretically sound but empirically unproven at scale.
Conservative approach: Base case uses median estimates across all three streams; sensitivity analysis demonstrates positive returns even at conservative QALY levels (565 billion DALYs (95% CI: 361 billion DALYs-877 billion DALYs) yields 637:1 (95% CI: 569:1-790:1) ROI using R&D savings alone).
Data Limitations
Military Spending Data
Global military expenditure data ($2.72T, SIPRI 2024) is well-documented but:
- Off-budget spending: Some military expenditures may be classified or categorized elsewhere
- Exchange rate fluctuations: Multi-year projections require currency assumptions
- Conflict zones: Military spending in active conflict regions may be less fungible for redirection
Clinical Trial Market Sizing
The $60B (95% CI: $50B-$75B)42 global clinical trials market estimate derives from industry reports, which:
- Industry variation: Methodologies vary across market research firms
- Private vs. public trials: Some trial spending may be unreported or proprietary
- Non-pharmaceutical trials: Medical device and digital health trials may have different cost structures
QALY Valuation Thresholds
Standard willingness-to-pay thresholds ($50K-$150K (95% CI: $100K-$199K)91 per QALY) vary by jurisdiction:
- Geographic variation: WHO recommends 1-3× GDP per capita; high-income countries use higher thresholds
- Ethical considerations: Monetary QALY valuations raise equity concerns
- Discount rates: Future health benefits discounted at 3% may undervalue long-term gains
Generalizability Constraints
Political Feasibility
This analysis models economic returns conditional on treaty ratification. Political feasibility depends on:
- Geopolitical stability: International cooperation requirements may face challenges during periods of global tension
- Domestic politics: Military budget reductions face constituency resistance in military-dependent regions
- Lobbying influence: Military industry opposition may impede adoption
Risk assessment: The 1% reduction is intentionally modest to minimize political resistance. Historical precedents (military-to-civilian conversions post-Cold War) demonstrate feasibility.
Institutional Capacity
Implementation requires substantial institutional development:
- Regulatory expertise: The framework requires experienced personnel (FDA, EMA, other regulators) to enable integration with existing regulatory frameworks
- Technical infrastructure: Data systems, AI/ML capabilities, cybersecurity at global scale
- Legal frameworks: International treaties, data privacy compliance, intellectual property harmonization
Mitigation: Phased implementation allows capacity building concurrent with scale-up.
Healthcare System Integration
Benefits assume integration with existing healthcare infrastructure:
- EHR interoperability: U.S. and other jurisdictions still face significant interoperability challenges
- Wearable adoption: Real-world data collection requires widespread wearable/digital health adoption
- Provider participation: Clinician buy-in necessary for trial recruitment and data quality
Uncertainty Quantification
Primary Risk Factors
The following table summarizes key risk factors and their mitigation strategies:
| Political Risk |
VERY HIGH |
Treaty ratification dependent on international coordination |
Modest 1% reduction; precedent from military-industrial lobbying ROI (1,813:1) |
| Execution Risk |
HIGH |
Complex global legal/technical coordination required |
Phased implementation; leverage existing regulatory expertise |
| Regulatory Risk |
MEDIUM-HIGH |
Harmonization across jurisdictions varies |
Pilot programs in willing jurisdictions first |
| Market Risk |
VERY LOW |
$2.72T48 military spending already allocated |
Redirection rather than new appropriation |
| Technical Risk |
MEDIUM |
Data interoperability, AI/ML accuracy |
Build on proven platforms (DCT platforms collectively raising $1B+ in VC funding) |
Scenario Analysis Robustness
Comprehensive sensitivity analysis across multiple scenarios demonstrates:
Robustness: Even under pessimistic assumptions with multiple adverse conditions simultaneously occurring, the intervention generates positive returns exceeding most established public health programs. The tornado chart for DFDA_EXPECTED_ROI shows that political success probability is the primary driver of uncertainty.
General Equilibrium Effects
This analysis employs partial equilibrium methodology, holding prices and market structures constant while evaluating the intervention’s direct effects. General equilibrium analysis would account for market adjustments to the $27.2B annual reallocation from military to pragmatic clinical trials spending.
Unmodeled general equilibrium effects include:
Data infrastructure scaling costs: Decentralized trial infrastructure uses automated software (federated queries, not centralized databases), scaling through technology rather than labor. Unlike traditional research that faces researcher supply constraints, the framework leverages existing EHR systems and adds coordination protocols. Marginal scaling costs are low relative to traditional models.
Clinical trial market price effects: Increasing trial demand by 12.3x (95% CI: 4.19x-61.3x) could affect equilibrium prices for clinical research services. However, the pragmatic trial approach reduces per-trial costs (82x (95% CI: 50x-94.1x) cheaper via automation), suggesting supply constraints may not bind. Traditional trials cost $41K (95% CI: $20K-$120K); decentralized trials target $929 (95% CI: $97-$3K) by eliminating overhead, not by increasing demand for scarce inputs.
Crowding out effects: Do billions in new pragmatic clinical trials displace existing research funding, or does it add incrementally? Conservative assumption: fully additive. If partially substitutive (e.g., governments reduce NIH funding in response), net research increase would be lower than modeled.
Quality versus quantity trade-off: 12.3x (95% CI: 4.19x-61.3x) more trials may not yield proportional breakthroughs if resources spread thin or trial quality declines. The analysis assumes quality maintenance through peer review and replication; actual quality effects remain uncertain.
Conservative treatment in base case: The analysis excludes general equilibrium effects from benefit calculations, providing a lower bound estimate.
Methodological limitation acknowledged: Full general equilibrium modeling (computable general equilibrium models with labor markets, international trade, and technology diffusion) would require substantial additional complexity beyond this analysis scope. The partial equilibrium approach follows standard cost-benefit analysis methodology for policy interventions.
Conditional Benefits Interpretation
The ROI estimates (637:1 (95% CI: 569:1-790:1) conservative, 84.8M:1 (95% CI: 46.6M:1-144M:1) complete) are conditional on successful implementation, they represent returns if the system operates as designed. Expected value analysis (see “Expected Value Analysis Accounting for Political Risk” section) incorporates probability-weighted scenarios. This section examines operational and technical failure modes that could occur even after political success, complementing the Investor Risk Analysis focus on political barriers. Pilot implementations should monitor false positive rates, adverse event detection sensitivity, regulatory acceptance rates, and industry adoption velocity to enable early course corrections.
Limitations Summary
Despite these limitations, several factors support the analysis’s robustness:
- Conservative assumptions throughout: Base case uses median estimates; optimistic scenarios excluded from primary ROI (637:1 (95% CI: 569:1-790:1))
- Empirical grounding: Cost reductions based on meta-analysis of 108 pragmatic trials132 plus large-scale implementations (RECOVERY, ADAPTABLE), not theoretical models
- Sensitivity analysis: Wide range of scenarios tested; positive returns maintained across all plausible parameter combinations
- Dominant intervention status: Cost-saving intervention ($0.0018 (95% CI: $0.0007-$0.0041) per DALY) means it saves money even if health benefits are substantially overstated
Transparency commitment: All parameters, data sources, and calculation methodologies are publicly documented with confidence levels and last-update dates in Parameters and Calculations Reference and References.
Future research priorities include prospective data collection during pilot implementations, real-world validation of cost reduction estimates, and longitudinal assessment of QALY gains across diverse populations and disease contexts.
Why This Differs from Failed Megaprojects
Large-scale interventions face legitimate skepticism. The development economics literature documents numerous failures: infrastructure megaprojects that exceed budgets by 50-100%, foreign aid programs with negative or negligible returns, and “grand challenges” that fail to materialize promised benefits.
This intervention differs in four critical ways:
Empirical grounding: Cost estimates based on demonstrated pragmatic trial results, not theoretical projections. Our projections use $929 (95% CI: $97-$3K)/patient based on the ADAPTABLE trial. (RECOVERY achieved $500 (95% CI: $400-$2.50K)/patient under exceptional NHS/COVID conditions; confidence interval captures this range.)
Decentralized execution: Unlike centralized megaprojects vulnerable to corruption and bureaucratic failure, pragmatic trials distribute decision-making across thousands of physicians and millions of patients. No single point of failure.
Cost-saving intervention status: Cost-saving interventions (reducing costs while improving outcomes) are robust to uncertainty in ways that cost-effective interventions are not. Even if health benefits are overstated by 50%, the intervention still saves money.
Aligned incentives: The 1% Treaty proposes Incentive Alignment Bonds: a single instrument that aligns investors (10% allocation, projected 272% returns), politicians (10% political incentive fund), and patients (80% pragmatic trials) with the same outcome, rather than relying on altruism or bureaucratic mandate.
Policy Implications
This analysis has direct implications for resource allocation decisions across multiple policy domains:
National Health Budgets
Traditional health budgets face impossible trade-offs: every dollar spent on cancer treatment is a dollar not spent on heart disease prevention. This intervention eliminates that constraint by redirecting funds from outside the health sector.
The opportunity: Health ministries can achieve 12.3x (95% CI: 4.19x-61.3x) more clinical research without reducing current health spending or raising taxes. The funding comes from military budgets, not health budgets.
Practical application: A nation spending $2.72T on military could redirect 1% ($27.2B) to fund pragmatic trials for its entire population while maintaining virtually all of its military capacity. The resulting health gains (416 million deaths (95% CI: 225 million deaths-630 million deaths) lives saved globally, proportional by population) far exceed any marginal security value of that 1%.
International Development Priorities
Development agencies face a fundamental problem: the most cost-effective interventions (bed nets at $89 (95% CI: $78-$100)/DALY, vaccines) can only scale linearly. Doubling impact requires doubling spending.
The difference: This intervention scales exponentially through systemic change. It doesn’t compete with existing development programs; it accelerates treatment discovery for all diseases affecting developing nations.
Practical application:
- Current approach: USAID spends billions on malaria bed nets (excellent intervention, $89 (95% CI: $78-$100)/DALY)
- Proposed addition: Support 1% treaty adoption, which delivers $0.0018 (95% CI: $0.0007-$0.0041)/DALY (50.3kx (95% CI: 23.7kx-111.7kx) better) while also funding research to eradicate malaria
- Result: Keep funding bed nets (they work!) AND accelerate development of malaria vaccines and treatments through massively expanded trial capacity
The Gates Foundation, USAID, and WHO should advocate for treaty adoption as their highest-leverage intervention: it multiplies the effectiveness of everything else they fund. The Gates Foundation’s historical pattern (spending billions on individual disease programs when the same capital could lobby for treaty passage and unlock $27.2B/year in government funding) exemplifies the “lottery tickets vs casino” problem described earlier. Advocacy for structural change offers superior ROI to direct program spending.
Military Budget Allocation
Military planners optimize for national security. This analysis demonstrates that 1% of military spending provides near-zero marginal security value while generating enormous economic returns when redirected.
The economic case: The fiscal multiplier (GDP generated per dollar spent) for military spending is 0.6x (95% CI: 0.4x-0.9x)26. Healthcare investment generates 4.3x (95% CI: 3x-6x)24, over 7.17x (95% CI: 6.83x-7.57x) higher. Beyond fiscal multipliers, medical research generates extraordinary health returns: economists Murphy and Topel found that longevity gains from medical advances are worth 50-100× the research investment155. Pragmatic trials, which produce 44.1x (95% CI: 39.4x-89.1x) more research output per dollar, multiply these already-massive returns.
Strategic perspective: A nation’s long-term security depends more on economic strength and healthy populations than on marginal weapons systems. Redirecting 1% from the $2.72T global military budget doesn’t compromise military (99% remains) but generates $172B (95% CI: $140B-$213B) in annual economic benefits.
Precedent: The U.S. spends more on military than the next 10 countries combined. A 1% reduction would still leave U.S. military spending higher than any potential adversary while funding 12.3x (95% CI: 4.19x-61.3x) more medical research globally.
Global Health Funding Mechanisms
Current global health funding relies on unpredictable philanthropic donations and limited government aid budgets. Total official development assistance for health: ~$40B/year. This intervention creates a $27.2B/year permanent funding stream.
Why this works: This is not charity; it’s profitable. Investors can purchase Incentive Alignment Bonds offering projected 272% backed by the peace dividend, making health funding financially attractive rather than dependent on altruism.
Mechanism design: The 1% Treaty Fund allocates:
- 80% ($21.8B) → pragmatic trials
- 10% ($2.72B) → bond investor returns
- 10% ($2.72B) → political incentive alignment
This creates a self-sustaining funding mechanism where: 1. Investors profit from peace dividend returns 2. Politicians profit from voter support and campaign funding 3. Pharma companies profit from massively reduced R&D costs 4. Patients benefit from 8.2 years (95% CI: 4.85 years-11.5 years) faster access to treatments 5. Governments benefit from healthier, more productive populations
Contrast with current system: WHO’s annual budget (~$6B) depends on voluntary contributions that can be cut at any time. The 1% Treaty creates a $27.2B/year legally-binding funding stream that grows automatically with military budgets.
Implementation Pathway
Policy adoption requires coordination across two levels:
- National level: Treaty advocacy through referendum campaigns ($250M) and lobbying ($650M)
- International level: UN General Assembly vote on binding treaty requiring 1% redirect from all signatory nations
Bottom Line for Policymakers
This intervention is cost-saving, making it one of the rarest findings in health economics. It doesn’t require:
- New taxes
- Reduced health spending
- Cuts to popular programs
- Technological breakthroughs
It requires only a 1% reallocation from the least cost-effective government spending (military) to the most cost-effective health intervention (pragmatic trials at $929 (95% CI: $97-$3K)/patient).
The political challenge isn’t economic: the ROI speaks for itself. The challenge is overcoming entrenched interests in military-industrial spending. The solution: Incentive Alignment Bonds that make supporting the treaty more profitable for politicians than opposing it.
Treaty Adoption: Political Will and Diplomatic Strategy
International treaty adoption is fundamentally a political and diplomatic process, not a technical implementation timeline. The 1% Treaty’s viability depends on simultaneous multilateral commitment: no nation reduces military spending unilaterally, creating security vulnerabilities or free-rider problems. All signatories reduce together.
Why Simultaneous Commitment Works: Escaping the Prisoner’s Dilemma
Unilateral military reduction is politically infeasible. This is a classic Prisoner’s Dilemma:
- If I reduce alone: Security vulnerability while others maintain full capacity (worst outcome)
- If I don’t reduce but others do: Free-ride on reduced conflict risk (tempting but unsustainable)
- If nobody reduces: Arms race continues, all players worse off (current equilibrium)
- If all reduce together: Maintain relative balance, redirect savings to health (optimal Nash equilibrium)
Simultaneous binding commitment solves the coordination problem: All signatories reduce 1% together, maintaining relative military balance while collectively redirecting $27.2B/year to health research that benefits all participants. The treaty converts a Prisoner’s Dilemma (where rational self-interest produces suboptimal outcomes) into a coordination game with enforceable commitments.
Historical Treaty Precedents
Successful international treaties achieved rapid adoption through diplomatic coalition-building, not phased pilots:
- Ottawa Landmine Ban Treaty (1997): Diplomatic push → international negotiation → 122 nations signed in 2 years
- Paris Climate Agreement (2015): Built on existing framework, achieved 195 signatories through coordinated diplomatic effort
- Chemical Weapons Convention (1993): International negotiation process, 193 state parties
Common pattern: Political will + coalition of willing nations + diplomatic negotiation → treaty adoption
The 1% Treaty follows this model, with the advantage that it offers immediate economic returns (637:1 (95% CI: 569:1-790:1) ROI minimum) rather than requiring sacrifice.
Adoption Pathway
Treaty adoption depends on: 1. Political coalition: Build support among health ministries, fiscal conservatives seeking budget efficiency, and populations demanding better healthcare 2. Economic case: 637:1 (95% CI: 569:1-790:1) ROI makes this profitable, not charitable 3. Incentive Alignment Bonds: Fund $1B advocacy phase, align investor and political incentives 4. Diplomatic negotiation: UN General Assembly or coalition of willing nations
Timeline: Highly variable depending on political momentum. Successful precedents range from 18 months (rapid consensus) to 5+ years (extended negotiation). The self-funding nature and aligned incentives favor faster adoption than typical treaties requiring sacrifice.
Conclusion
Redirecting 1% of global military spending to pragmatic clinical trials delivers 637:1 (95% CI: 569:1-790:1) to 84.8M:1 (95% CI: 46.6M:1-144M:1) ROI using standard health economics methodology (NPV, QALYs, ICER). The intervention qualifies as cost-saving and requires no new taxes, only reallocation of existing budgets to higher-ROI activities.
1.
NIH Common Fund. NIH pragmatic trials: Minimal funding despite 30x cost advantage.
NIH Common Fund: HCS Research Collaboratory https://commonfund.nih.gov/hcscollaboratory (2025)
The NIH Pragmatic Trials Collaboratory funds trials at $500K for planning phase, $1M/year for implementation-a tiny fraction of NIH’s budget. The ADAPTABLE trial cost $14 million for 15,076 patients (= $929/patient) versus $420 million for a similar traditional RCT (30x cheaper), yet pragmatic trials remain severely underfunded. PCORnet infrastructure enables real-world trials embedded in healthcare systems, but receives minimal support compared to basic research funding. Additional sources: https://commonfund.nih.gov/hcscollaboratory | https://pcornet.org/wp-content/uploads/2025/08/ADAPTABLE_Lay_Summary_21JUL2025.pdf | https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5604499/
.
2.
NIH. Antidepressant clinical trial exclusion rates.
Zimmerman et al. https://pubmed.ncbi.nlm.nih.gov/26276679/ (2015)
Mean exclusion rate: 86.1% across 158 antidepressant efficacy trials (range: 44.4% to 99.8%) More than 82% of real-world depression patients would be ineligible for antidepressant registration trials Exclusion rates increased over time: 91.4% (2010-2014) vs. 83.8% (1995-2009) Most common exclusions: comorbid psychiatric disorders, age restrictions, insufficient depression severity, medical conditions Emergency psychiatry patients: only 3.3% eligible (96.7% excluded) when applying 9 common exclusion criteria Only a minority of depressed patients seen in clinical practice are likely to be eligible for most AETs Note: Generalizability of antidepressant trials has decreased over time, with increasingly stringent exclusion criteria eliminating patients who would actually use the drugs in clinical practice Additional sources: https://pubmed.ncbi.nlm.nih.gov/26276679/ | https://pubmed.ncbi.nlm.nih.gov/26164052/ | https://www.wolterskluwer.com/en/news/antidepressant-trials-exclude-most-real-world-patients-with-depression
.
3.
CNBC. Warren buffett’s career average investment return.
CNBC https://www.cnbc.com/2025/05/05/warren-buffetts-return-tally-after-60-years-5502284percent.html (2025)
Berkshire’s compounded annual return from 1965 through 2024 was 19.9%, nearly double the 10.4% recorded by the S&P 500. Berkshire shares skyrocketed 5,502,284% compared to the S&P 500’s 39,054% rise during that period. Additional sources: https://www.cnbc.com/2025/05/05/warren-buffetts-return-tally-after-60-years-5502284percent.html | https://www.slickcharts.com/berkshire-hathaway/returns
.
4.
World Health Organization. WHO global health estimates 2024.
World Health Organization https://www.who.int/data/gho/data/themes/mortality-and-global-health-estimates (2024)
Comprehensive mortality and morbidity data by cause, age, sex, country, and year Global mortality: 55-60 million deaths annually Lives saved by modern medicine (vaccines, cardiovascular drugs, oncology): 12M annually (conservative aggregate) Leading causes of death: Cardiovascular disease (17.9M), Cancer (10.3M), Respiratory disease (4.0M) Note: Baseline data for regulatory mortality analysis. Conservative estimate of pharmaceutical impact based on WHO immunization data (4.5M/year from vaccines) + cardiovascular interventions (3.3M/year) + oncology (1.5M/year) + other therapies. Additional sources: https://www.who.int/data/gho/data/themes/mortality-and-global-health-estimates
.
5.
GiveWell. GiveWell cost per life saved for top charities (2024).
GiveWell: Top Charities https://www.givewell.org/charities/top-charities General range: $3,000-$5,500 per life saved (GiveWell top charities) Helen Keller International (Vitamin A): $3,500 average (2022-2024); varies $1,000-$8,500 by country Against Malaria Foundation: $5,500 per life saved New Incentives (vaccination incentives): $4,500 per life saved Malaria Consortium (seasonal malaria chemoprevention): $3,500 per life saved VAS program details: $2 to provide vitamin A supplements to child for one year Note: Figures accurate for 2024. Helen Keller VAS program has wide country variation ($1K-$8.5K) but $3,500 is accurate average. Among most cost-effective interventions globally Additional sources: https://www.givewell.org/charities/top-charities | https://www.givewell.org/charities/helen-keller-international | https://ourworldindata.org/cost-effectiveness
.
6.
AARP. Unpaid caregiver hours and economic value.
AARP 2023 https://www.aarp.org/caregiving/financial-legal/info-2023/unpaid-caregivers-provide-billions-in-care.html (2023)
Average family caregiver: 25-26 hours per week (100-104 hours per month) 38 million caregivers providing 36 billion hours of care annually Economic value: $16.59 per hour = $600 billion total annual value (2021) 28% of people provided eldercare on a given day, averaging 3.9 hours when providing care Caregivers living with care recipient: 37.4 hours per week Caregivers not living with recipient: 23.7 hours per week Note: Disease-related caregiving is subset of total; includes elderly care, disability care, and child care Additional sources: https://www.aarp.org/caregiving/financial-legal/info-2023/unpaid-caregivers-provide-billions-in-care.html | https://www.bls.gov/news.release/elcare.nr0.htm | https://www.caregiver.org/resource/caregiver-statistics-demographics/
.
7.
MMWR, C. Childhood vaccination economic benefits.
CDC MMWR https://www.cdc.gov/mmwr/volumes/73/wr/mm7331a2.htm (1994)
US programs (1994-2023): $540B direct savings, $2.7T societal savings ( $18B/year direct, $90B/year societal) Global (2001-2020): $820B value for 10 diseases in 73 countries ( $41B/year) ROI: $11 return per $1 invested Measles vaccination alone saved 93.7M lives (61% of 154M total) over 50 years (1974-2024) Additional sources: https://www.cdc.gov/mmwr/volumes/73/wr/mm7331a2.htm | https://www.thelancet.com/journals/lancet/article/PIIS0140-6736(24)00850-X/fulltext
.
9.
Labor Statistics, U. S. B. of.
CPI inflation calculator. (2024)
CPI-U (1980): 82.4 CPI-U (2024): 313.5 Inflation multiplier (1980-2024): 3.80× Cumulative inflation: 280.48% Average annual inflation rate: 3.08% Note: Official U.S. government inflation data using Consumer Price Index for All Urban Consumers (CPI-U). Additional sources: https://www.bls.gov/data/inflation_calculator.htm
.
10.
ClinicalTrials.gov API v2 direct analysis. ClinicalTrials.gov cumulative enrollment data (2025).
Direct analysis via ClinicalTrials.gov API v2 https://clinicaltrials.gov/data-api/api Analysis of 100,000 active/recruiting/completed trials on ClinicalTrials.gov (as of January 2025) shows cumulative enrollment of 12.2 million participants: Phase 1 (722k), Phase 2 (2.2M), Phase 3 (6.5M), Phase 4 (2.7M). Median participants per trial: Phase 1 (33), Phase 2 (60), Phase 3 (237), Phase 4 (90). Additional sources: https://clinicaltrials.gov/data-api/api
.
11.
CAN, A. Clinical trial patient participation rate.
ACS CAN: Barriers to Clinical Trial Enrollment https://www.fightcancer.org/policy-resources/barriers-patient-enrollment-therapeutic-clinical-trials-cancer Only 3-5% of adult cancer patients in US receive treatment within clinical trials About 5% of American adults have ever participated in any clinical trial Oncology: 2-3% of all oncology patients participate Contrast: 50-60% enrollment for pediatric cancer trials (<15 years old) Note: 20% of cancer trials fail due to insufficient enrollment; 11% of research sites enroll zero patients Additional sources: https://www.fightcancer.org/policy-resources/barriers-patient-enrollment-therapeutic-clinical-trials-cancer | https://hints.cancer.gov/docs/Briefs/HINTS_Brief_48.pdf
.
12.
ScienceDaily. Global prevalence of chronic disease.
ScienceDaily: GBD 2015 Study https://www.sciencedaily.com/releases/2015/06/150608081753.htm (2015)
2.3 billion individuals had more than five ailments (2013) Chronic conditions caused 74% of all deaths worldwide (2019), up from 67% (2010) Approximately 1 in 3 adults suffer from multiple chronic conditions (MCCs) Risk factor exposures: 2B exposed to biomass fuel, 1B to air pollution, 1B smokers Projected economic cost: $47 trillion by 2030 Note: 2.3B with 5+ ailments is more accurate than "2B with chronic disease." One-third of all adults globally have multiple chronic conditions Additional sources: https://www.sciencedaily.com/releases/2015/06/150608081753.htm | https://pmc.ncbi.nlm.nih.gov/articles/PMC10830426/ | https://pmc.ncbi.nlm.nih.gov/articles/PMC6214883/
.
13.
C&EN. Annual number of new drugs approved globally: 50.
C&EN https://cen.acs.org/pharmaceuticals/50-new-drugs-received-FDA/103/i2 (2025)
50 new drugs approved annually Additional sources: https://cen.acs.org/pharmaceuticals/50-new-drugs-received-FDA/103/i2 | https://www.fda.gov/drugs/development-approval-process-drugs/novel-drug-approvals-fda
.
14.
Williams, R. J., Tse, T., DiPiazza, K. & Zarin, D. A.
Terminated trials in the ClinicalTrials.gov results database: Evaluation of availability of primary outcome data and reasons for termination.
PLOS One 10, e0127242 (2015)
Approximately 12% of trials with results posted on the ClinicalTrials.gov results database (905/7,646) were terminated. Primary reasons: insufficient accrual (57% of non-data-driven terminations), business/strategic reasons, and efficacy/toxicity findings (21% data-driven terminations).
18.
GiveWell. Cost per DALY for deworming programs.
https://www.givewell.org/international/technical/programs/deworming/cost-effectiveness Schistosomiasis treatment: $28.19-$70.48 per DALY (using arithmetic means with varying disability weights) Soil-transmitted helminths (STH) treatment: $82.54 per DALY (midpoint estimate) Note: GiveWell explicitly states this 2011 analysis is "out of date" and their current methodology focuses on long-term income effects rather than short-term health DALYs Additional sources: https://www.givewell.org/international/technical/programs/deworming/cost-effectiveness
.
20.
Think by Numbers. Pre-1962 drug development costs and timeline (think by numbers).
Think by Numbers: How Many Lives Does FDA Save? https://thinkbynumbers.org/health/how-many-net-lives-does-the-fda-save/ (1962)
Historical estimates (1970-1985): USD $226M fully capitalized (2011 prices) 1980s drugs: $65M after-tax R&D (1990 dollars), $194M compounded to approval (1990 dollars) Modern comparison: $2-3B costs, 7-12 years (dramatic increase from pre-1962) Context: 1962 regulatory clampdown reduced new treatment production by 70%, dramatically increasing development timelines and costs Note: Secondary source; less reliable than Congressional testimony Additional sources: https://thinkbynumbers.org/health/how-many-net-lives-does-the-fda-save/ | https://en.wikipedia.org/wiki/Cost_of_drug_development | https://www.statnews.com/2018/10/01/changing-1962-law-slash-drug-prices/
.
21.
(BIO), B. I. O. BIO clinical development success rates 2011-2020.
Biotechnology Innovation Organization (BIO) https://go.bio.org/rs/490-EHZ-999/images/ClinicalDevelopmentSuccessRates2011_2020.pdf (2021)
Phase I duration: 2.3 years average Total time to market (Phase I-III + approval): 10.5 years average Phase transition success rates: Phase I→II: 63.2%, Phase II→III: 30.7%, Phase III→Approval: 58.1% Overall probability of approval from Phase I: 12% Note: Largest publicly available study of clinical trial success rates. Efficacy lag = 10.5 - 2.3 = 8.2 years post-safety verification. Additional sources: https://go.bio.org/rs/490-EHZ-999/images/ClinicalDevelopmentSuccessRates2011_2020.pdf
.
22.
Medicine, N. Drug repurposing rate ( 30%).
Nature Medicine https://www.nature.com/articles/s41591-024-03233-x (2024)
Approximately 30% of drugs gain at least one new indication after initial approval. Additional sources: https://www.nature.com/articles/s41591-024-03233-x
.
23.
EPI. Education investment economic multiplier (2.1).
EPI: Public Investments Outside Core Infrastructure https://www.epi.org/publication/bp348-public-investments-outside-core-infrastructure/ Early childhood education: Benefits 12X outlays by 2050; $8.70 per dollar over lifetime Educational facilities: $1 spent → $1.50 economic returns Energy efficiency comparison: 2-to-1 benefit-to-cost ratio (McKinsey) Private return to schooling: 9% per additional year (World Bank meta-analysis) Note: 2.1 multiplier aligns with benefit-to-cost ratios for educational infrastructure/energy efficiency. Early childhood education shows much higher returns (12X by 2050) Additional sources: https://www.epi.org/publication/bp348-public-investments-outside-core-infrastructure/ | https://documents1.worldbank.org/curated/en/442521523465644318/pdf/WPS8402.pdf | https://freopp.org/whitepapers/establishing-a-practical-return-on-investment-framework-for-education-and-skills-development-to-expand-economic-opportunity/
.
24.
PMC. Healthcare investment economic multiplier (1.8).
PMC: California Universal Health Care https://pmc.ncbi.nlm.nih.gov/articles/PMC5954824/ (2022)
Healthcare fiscal multiplier: 4.3 (95% CI: 2.5-6.1) during pre-recession period (1995-2007) Overall government spending multiplier: 1.61 (95% CI: 1.37-1.86) Why healthcare has high multipliers: No effect on trade deficits (spending stays domestic); improves productivity & competitiveness; enhances long-run potential output Gender-sensitive fiscal spending (health & care economy) produces substantial positive growth impacts Note: "1.8" appears to be conservative estimate; research shows healthcare multipliers of 4.3 Additional sources: https://pmc.ncbi.nlm.nih.gov/articles/PMC5954824/ | https://cepr.org/voxeu/columns/government-investment-and-fiscal-stimulus | https://ncbi.nlm.nih.gov/pmc/articles/PMC3849102/ | https://set.odi.org/wp-content/uploads/2022/01/Fiscal-multipliers-review.pdf
.
25.
World Bank. Infrastructure investment economic multiplier (1.6).
World Bank: Infrastructure Investment as Stimulus https://blogs.worldbank.org/en/ppps/effectiveness-infrastructure-investment-fiscal-stimulus-what-weve-learned (2022)
Infrastructure fiscal multiplier: 1.6 during contractionary phase of economic cycle Average across all economic states: 1.5 (meaning $1 of public investment → $1.50 of economic activity) Time horizon: 0.8 within 1 year, 1.5 within 2-5 years Range of estimates: 1.5-2.0 (following 2008 financial crisis & American Recovery Act) Italian public construction: 1.5-1.9 multiplier US ARRA: 0.4-2.2 range (differential impacts by program type) Economic Policy Institute: Uses 1.6 for infrastructure spending (middle range of estimates) Note: Public investment less likely to crowd out private activity during recessions; particularly effective when monetary policy loose with near-zero rates Additional sources: https://blogs.worldbank.org/en/ppps/effectiveness-infrastructure-investment-fiscal-stimulus-what-weve-learned | https://www.gihub.org/infrastructure-monitor/insights/fiscal-multiplier-effect-of-infrastructure-investment/ | https://cepr.org/voxeu/columns/government-investment-and-fiscal-stimulus | https://www.richmondfed.org/publications/research/economic_brief/2022/eb_22-04
.
26.
Mercatus. Military spending economic multiplier (0.6).
Mercatus: Defense Spending and Economy https://www.mercatus.org/research/research-papers/defense-spending-and-economy Ramey (2011): 0.6 short-run multiplier Barro (1981): 0.6 multiplier for WWII spending (war spending crowded out 40¢ private economic activity per federal dollar) Barro & Redlick (2011): 0.4 within current year, 0.6 over two years; increased govt spending reduces private-sector GDP portions General finding: $1 increase in deficit-financed federal military spending = less than $1 increase in GDP Variation by context: Central/Eastern European NATO: 0.6 on impact, 1.5-1.6 in years 2-3, gradual fall to zero Ramey & Zubairy (2018): Cumulative 1% GDP increase in military expenditure raises GDP by 0.7% Additional sources: https://www.mercatus.org/research/research-papers/defense-spending-and-economy | https://cepr.org/voxeu/columns/world-war-ii-america-spending-deficits-multipliers-and-sacrifice | https://www.rand.org/content/dam/rand/pubs/research_reports/RRA700/RRA739-2/RAND_RRA739-2.pdf
.
27.
FDA. FDA-approved prescription drug products (20,000+).
FDA https://www.fda.gov/media/143704/download There are over 20,000 prescription drug products approved for marketing. Additional sources: https://www.fda.gov/media/143704/download
.
29.
ACLED. Active combat deaths annually.
ACLED: Global Conflict Surged 2024 https://acleddata.com/2024/12/12/data-shows-global-conflict-surged-in-2024-the-washington-post/ (2024)
2024: 233,597 deaths (30% increase from 179,099 in 2023) Deadliest conflicts: Ukraine (67,000), Palestine (35,000) Nearly 200,000 acts of violence (25% higher than 2023, double from 5 years ago) One in six people globally live in conflict-affected areas Additional sources: https://acleddata.com/2024/12/12/data-shows-global-conflict-surged-in-2024-the-washington-post/ | https://acleddata.com/media-citation/data-shows-global-conflict-surged-2024-washington-post | https://acleddata.com/conflict-index/index-january-2024/
.
30.
UCDP. State violence deaths annually.
UCDP: Uppsala Conflict Data Program https://ucdp.uu.se/ Uppsala Conflict Data Program (UCDP): Tracks one-sided violence (organized actors attacking unarmed civilians) UCDP definition: Conflicts causing at least 25 battle-related deaths in calendar year 2023 total organized violence: 154,000 deaths; Non-state conflicts: 20,900 deaths UCDP collects data on state-based conflicts, non-state conflicts, and one-sided violence Specific "2,700 annually" figure for state violence not found in recent UCDP data; actual figures vary annually Additional sources: https://ucdp.uu.se/ | https://en.wikipedia.org/wiki/Uppsala_Conflict_Data_Program | https://ourworldindata.org/grapher/deaths-in-armed-conflicts-by-region
.
31.
Our World in Data. Terror attack deaths (8,300 annually).
Our World in Data: Terrorism https://ourworldindata.org/terrorism (2024)
2023: 8,352 deaths (22% increase from 2022, highest since 2017) 2023: 3,350 terrorist incidents (22% decrease), but 56% increase in avg deaths per attack Global Terrorism Database (GTD): 200,000+ terrorist attacks recorded (2021 version) Maintained by: National Consortium for Study of Terrorism & Responses to Terrorism (START), U. of Maryland Geographic shift: Epicenter moved from Middle East to Central Sahel (sub-Saharan Africa) - now >50% of all deaths Additional sources: https://ourworldindata.org/terrorism | https://reliefweb.int/report/world/global-terrorism-index-2024 | https://www.start.umd.edu/gtd/ | https://ourworldindata.org/grapher/fatalities-from-terrorism
.
32.
Institute for Health Metrics and Evaluation (IHME). IHME global burden of disease 2021 (2.88B DALYs, 1.13B YLD).
Institute for Health Metrics and Evaluation (IHME) https://vizhub.healthdata.org/gbd-results/ (2024)
In 2021, global DALYs totaled approximately 2.88 billion, comprising 1.75 billion Years of Life Lost (YLL) and 1.13 billion Years Lived with Disability (YLD). This represents a 13% increase from 2019 (2.55B DALYs), largely attributable to COVID-19 deaths and aging populations. YLD accounts for approximately 39% of total DALYs, reflecting the substantial burden of non-fatal chronic conditions. Additional sources: https://vizhub.healthdata.org/gbd-results/ | https://www.thelancet.com/journals/lancet/article/PIIS0140-6736(24)00757-8/fulltext | https://www.healthdata.org/research-analysis/about-gbd
.
33.
Costs of War Project, Brown University Watson Institute. Environmental cost of war ($100B annually).
Brown Watson Costs of War: Environmental Cost https://watson.brown.edu/costsofwar/costs/social/environment War on Terror emissions: 1.2B metric tons GHG (equivalent to 257M cars/year) Military: 5.5% of global GHG emissions (2X aviation + shipping combined) US DoD: World’s single largest institutional oil consumer, 47th largest emitter if nation Cleanup costs: $500B+ for military contaminated sites Gaza war environmental damage: $56.4B; landmine clearance: $34.6B expected Climate finance gap: Rich nations spend 30X more on military than climate finance Note: Military activities cause massive environmental damage through GHG emissions, toxic contamination, and long-term cleanup costs far exceeding current climate finance commitments Additional sources: https://watson.brown.edu/costsofwar/costs/social/environment | https://earth.org/environmental-costs-of-wars/ | https://transformdefence.org/transformdefence/stats/
.
34.
ScienceDaily. Medical research lives saved annually (4.2 million).
ScienceDaily: Physical Activity Prevents 4M Deaths https://www.sciencedaily.com/releases/2020/06/200617194510.htm (2020)
Physical activity: 3.9M early deaths averted annually worldwide (15% lower premature deaths than without) COVID vaccines (2020-2024): 2.533M deaths averted, 14.8M life-years preserved; first year alone: 14.4M deaths prevented Cardiovascular prevention: 3 interventions could delay 94.3M deaths over 25 years (antihypertensives alone: 39.4M) Pandemic research response: Millions of deaths averted through rapid vaccine/drug development Additional sources: https://www.sciencedaily.com/releases/2020/06/200617194510.htm | https://pmc.ncbi.nlm.nih.gov/articles/PMC9537923/ | https://www.ahajournals.org/doi/10.1161/CIRCULATIONAHA.118.038160 | https://pmc.ncbi.nlm.nih.gov/articles/PMC9464102/
.
35.
SIPRI. 36:1 disparity ratio of spending on weapons over cures.
SIPRI: Military Spending https://www.sipri.org/commentary/blog/2016/opportunity-cost-world-military-spending (2016)
Global military spending: $2.7 trillion (2024, SIPRI) Global government medical research: $68 billion (2024) Actual ratio: 39.7:1 in favor of weapons over medical research Military R&D alone: $85B (2004 data, 10% of global R&D) Military spending increases crowd out health: 1% ↑ military = 0.62% ↓ health spending Note: Ratio actually worse than 36:1. Each 1% increase in military spending reduces health spending by 0.62%, with effect more intense in poorer countries (0.962% reduction) Additional sources: https://www.sipri.org/commentary/blog/2016/opportunity-cost-world-military-spending | https://pmc.ncbi.nlm.nih.gov/articles/PMC9174441/ | https://www.congress.gov/crs-product/R45403
.
36.
Think by Numbers. Lost human capital due to war ($270B annually).
Think by Numbers: War Costs $74 https://thinkbynumbers.org/military/war/the-economic-case-for-peace-a-comprehensive-financial-analysis/ (2021)
Lost human capital from war: $300B annually (economic impact of losing skilled/productive individuals to conflict) Broader conflict/violence cost: $14T/year globally 1.4M violent deaths/year; conflict holds back economic development, causes instability, widens inequality, erodes human capital 2002: 48.4M DALYs lost from 1.6M violence deaths = $151B economic value (2000 USD) Economic toll includes: commodity prices, inflation, supply chain disruption, declining output, lost human capital Additional sources: https://thinkbynumbers.org/military/war/the-economic-case-for-peace-a-comprehensive-financial-analysis/ | https://www.weforum.org/stories/2021/02/war-violence-costs-each-human-5-a-day/ | https://pubmed.ncbi.nlm.nih.gov/19115548/
.
37.
PubMed. Psychological impact of war cost ($100B annually).
PubMed: Economic Burden of PTSD https://pubmed.ncbi.nlm.nih.gov/35485933/ PTSD economic burden (2018 U.S.): $232.2B total ($189.5B civilian, $42.7B military) Civilian costs driven by: Direct healthcare ($66B), unemployment ($42.7B) Military costs driven by: Disability ($17.8B), direct healthcare ($10.1B) Exceeds costs of other mental health conditions (anxiety, depression) War-exposed populations: 2-3X higher rates of anxiety, depression, PTSD; women and children most vulnerable Note: Actual burden $232B, significantly higher than "$100B" claimed Additional sources: https://pubmed.ncbi.nlm.nih.gov/35485933/ | https://news.va.gov/103611/study-national-economic-burden-of-ptsd-staggering/ | https://pmc.ncbi.nlm.nih.gov/articles/PMC9957523/
.
38.
CGDev. UNHCR average refugee support cost.
CGDev https://www.cgdev.org/blog/costs-hosting-refugees-oecd-countries-and-why-uk-outlier (2024)
The average cost of supporting a refugee is $1,384 per year. This represents total host country costs (housing, healthcare, education, security). OECD countries average $6,100 per refugee (mean 2022-2023), with developing countries spending $700-1,000. Global weighted average of $1,384 is reasonable given that 75-85% of refugees are in low/middle-income countries. Additional sources: https://www.cgdev.org/blog/costs-hosting-refugees-oecd-countries-and-why-uk-outlier | https://www.unhcr.org/sites/default/files/2024-11/UNHCR-WB-global-cost-of-refugee-inclusion-in-host-country-health-systems.pdf
.
39.
World Bank. World bank trade disruption cost from conflict.
World Bank https://www.worldbank.org/en/topic/trade/publication/trading-away-from-conflict Estimated $616B annual cost from conflict-related trade disruption. World Bank research shows civil war costs an average developing country 30 years of GDP growth, with 20 years needed for trade to return to pre-war levels. Trade disputes analysis shows tariff escalation could reduce global exports by up to $674 billion. Additional sources: https://www.worldbank.org/en/topic/trade/publication/trading-away-from-conflict | https://www.nber.org/papers/w11565 | http://blogs.worldbank.org/en/trade/impacts-global-trade-and-income-current-trade-disputes
.
40.
VA. Veteran healthcare cost projections.
VA https://department.va.gov/wp-content/uploads/2025/06/2026-Budget-in-Brief.pdf (2026)
VA budget: $441.3B requested for FY 2026 (10% increase). Disability compensation: $165.6B in FY 2024 for 6.7M veterans. PACT Act projected to increase spending by $300B between 2022-2031. Costs under Toxic Exposures Fund: $20B (2024), $30.4B (2025), $52.6B (2026). Additional sources: https://department.va.gov/wp-content/uploads/2025/06/2026-Budget-in-Brief.pdf | https://www.cbo.gov/publication/45615 | https://www.legion.org/information-center/news/veterans-healthcare/2025/june/va-budget-tops-400-billion-for-2025-from-higher-spending-on-mandated-benefits-medical-care
.
43.
Calculated from IHME Global Burden of Disease (2.55B DALYs) and global GDP per capita valuation. $109 trillion annual global disease burden.
The global economic burden of disease, including direct healthcare costs ($8.2 trillion) and lost productivity ($100.9 trillion from 2.55 billion DALYs × $39,570 per DALY), totals approximately $109.1 trillion annually.
45.
Trials, A. C. Global government spending on interventional clinical trials: $3-6 billion/year.
Applied Clinical Trials https://www.appliedclinicaltrialsonline.com/view/sizing-clinical-research-market Estimated range based on NIH ( $0.8-5.6B), NIHR ($1.6B total budget), and EU funding ( $1.3B/year). Roughly 5-10% of global market. Additional sources: https://www.appliedclinicaltrialsonline.com/view/sizing-clinical-research-market | https://www.thelancet.com/journals/langlo/article/PIIS2214-109X(20)30357-0/fulltext
.
49.
Estimated from major foundation budgets and activities. Nonprofit clinical trial funding estimate.
Nonprofit foundations spend an estimated $2-5 billion annually on clinical trials globally, representing approximately 2-5% of total clinical trial spending.
50.
IQVIA, I. reports: Global pharmaceutical r&d spending.
Total global pharmaceutical R&D spending is approximately $300 billion annually. Clinical trials represent 15-20% of this total ($45-60B), with the remainder going to drug discovery, preclinical research, regulatory affairs, and manufacturing development.
51.
UN. Global population reaches 8 billion.
UN: World Population 8 Billion Nov 15 2022 https://www.un.org/en/desa/world-population-reach-8-billion-15-november-2022 (2022)
Milestone: November 15, 2022 (UN World Population Prospects 2022) Day of Eight Billion" designated by UN Added 1 billion people in just 11 years (2011-2022) Growth rate: Slowest since 1950; fell under 1% in 2020 Future: 15 years to reach 9B (2037); projected peak 10.4B in 2080s Projections: 8.5B (2030), 9.7B (2050), 10.4B (2080-2100 plateau) Note: Milestone reached Nov 2022. Population growth slowing; will take longer to add next billion (15 years vs 11 years) Additional sources: https://www.un.org/en/desa/world-population-reach-8-billion-15-november-2022 | https://www.un.org/en/dayof8billion | https://en.wikipedia.org/wiki/Day_of_Eight_Billion
.
52.
Harvard Kennedy School. 3.5% participation tipping point.
Harvard Kennedy School https://www.hks.harvard.edu/centers/carr/publications/35-rule-how-small-minority-can-change-world (2020)
The research found that nonviolent campaigns were twice as likely to succeed as violent ones, and once 3.5% of the population were involved, they were always successful. Chenoweth and Maria Stephan studied the success rates of civil resistance efforts from 1900 to 2006, finding that nonviolent movements attracted, on average, four times as many participants as violent movements and were more likely to succeed. Key finding: Every campaign that mobilized at least 3.5% of the population in sustained protest was successful (in their 1900-2006 dataset) Note: The 3.5% figure is a descriptive statistic from historical analysis, not a guaranteed threshold. One exception (Bahrain 2011-2014 with 6%+ participation) has been identified. The rule applies to regime change, not policy change in democracies. Additional sources: https://www.hks.harvard.edu/centers/carr/publications/35-rule-how-small-minority-can-change-world | https://www.hks.harvard.edu/sites/default/files/2024-05/Erica%20Chenoweth_2020-005.pdf | https://www.bbc.com/future/article/20190513-it-only-takes-35-of-people-to-change-the-world | https://en.wikipedia.org/wiki/3.5%25_rule
.
53.
NHGRI. Human genome project and CRISPR discovery.
NHGRI https://www.genome.gov/11006929/2003-release-international-consortium-completes-hgp (2003)
Your DNA is 3 billion base pairs Read the entire code (Human Genome Project, completed 2003) Learned to edit it (CRISPR, discovered 2012) Additional sources: https://www.genome.gov/11006929/2003-release-international-consortium-completes-hgp | https://www.nobelprize.org/prizes/chemistry/2020/press-release/
.
54.
PMC. Only 12% of human interactome targeted.
PMC https://pmc.ncbi.nlm.nih.gov/articles/PMC10749231/ (2023)
Mapping 350,000+ clinical trials showed that only 12% of the human interactome has ever been targeted by drugs. Additional sources: https://pmc.ncbi.nlm.nih.gov/articles/PMC10749231/
.
55.
WHO. ICD-10 code count ( 14,000).
WHO https://icd.who.int/browse10/2019/en (2019)
The ICD-10 classification contains approximately 14,000 codes for diseases, signs and symptoms. Additional sources: https://icd.who.int/browse10/2019/en
.
56.
Wikipedia. Longevity escape velocity (LEV) - maximum human life extension potential.
Wikipedia: Longevity Escape Velocity https://en.wikipedia.org/wiki/Longevity_escape_velocity Longevity escape velocity: Hypothetical point where medical advances extend life expectancy faster than time passes Term coined by Aubrey de Grey (biogerontologist) in 2004 paper; concept from David Gobel (Methuselah Foundation) Current progress: Science adds 3 months to lifespan per year; LEV requires adding >1 year per year Sinclair (Harvard): "There is no biological upper limit to age" - first person to live to 150 may already be born De Grey: 50% chance of reaching LEV by mid-to-late 2030s; SENS approach = damage repair rather than slowing damage Kurzweil (2024): LEV by 2029-2035, AI will simulate biological processes to accelerate solutions George Church: LEV "in a decade or two" via age-reversal clinical trials Natural lifespan cap: 120-150 years (Jeanne Calment record: 122); engineering approach could bypass via damage repair Key mechanisms: Epigenetic reprogramming, senolytic drugs, stem cell therapy, gene therapy, AI-driven drug discovery Current record: Jeanne Calment (122 years, 164 days) - record unbroken since 1997 Note: LEV is theoretical but increasingly plausible given demonstrated age reversal in mice (109% lifespan extension) and human cells (30-year epigenetic age reversal) Additional sources: https://en.wikipedia.org/wiki/Longevity_escape_velocity | https://pmc.ncbi.nlm.nih.gov/articles/PMC423155/ | https://www.popularmechanics.com/science/a36712084/can-science-cure-death-longevity/ | https://www.diamandis.com/blog/longevity-escape-velocity
.
57.
OpenSecrets. Lobbyist statistics for washington d.c.
OpenSecrets: Lobbying in US https://en.wikipedia.org/wiki/Lobbying_in_the_United_States Registered lobbyists: Over 12,000 (some estimates); 12,281 registered (2013) Former government employees as lobbyists: 2,200+ former federal employees (1998-2004), including 273 former White House staffers, 250 former Congress members & agency heads Congressional revolving door: 43% (86 of 198) lawmakers who left 1998-2004 became lobbyists; currently 59% leaving to private sector work for lobbying/consulting firms/trade groups Executive branch: 8% were registered lobbyists at some point before/after government service Additional sources: https://en.wikipedia.org/wiki/Lobbying_in_the_United_States | https://www.opensecrets.org/revolving-door | https://www.citizen.org/article/revolving-congress/ | https://www.propublica.org/article/we-found-a-staggering-281-lobbyists-whove-worked-in-the-trump-administration
.
58.
Vaccines, M. Measles vaccination ROI.
MDPI Vaccines https://www.mdpi.com/2076-393X/12/11/1210 (2024)
Single measles vaccination: 167:1 benefit-cost ratio. MMR (measles-mumps-rubella) vaccination: 14:1 ROI. Historical US elimination efforts (1966-1974): benefit-cost ratio of 10.3:1 with net benefits exceeding USD 1.1 billion (1972 dollars, or USD 8.0 billion in 2023 dollars). 2-dose MMR programs show direct benefit/cost ratio of 14.2 with net savings of $5.3 billion, and 26.0 from societal perspectives with net savings of $11.6 billion. Additional sources: https://www.mdpi.com/2076-393X/12/11/1210 | https://www.tandfonline.com/doi/full/10.1080/14760584.2024.2367451
.
62.
Calculated from Orphanet Journal of Rare Diseases (2024). Diseases getting first effective treatment each year.
Calculated from Orphanet Journal of Rare Diseases (2024) https://ojrd.biomedcentral.com/articles/10.1186/s13023-024-03398-1 (2024)
Under the current system, approximately 10-15 diseases per year receive their FIRST effective treatment. Calculation: 5% of 7,000 rare diseases ( 350) have FDA-approved treatment, accumulated over 40 years of the Orphan Drug Act = 9 rare diseases/year. Adding 5-10 non-rare diseases that get first treatments yields 10-20 total. FDA approves 50 drugs/year, but many are for diseases that already have treatments (me-too drugs, second-line therapies). Only 15 represent truly FIRST treatments for previously untreatable conditions.
63.
NIH. NIH budget (FY 2025).
NIH https://www.nih.gov/about-nih/organization/budget (2024)
The budget total of $47.7 billion also includes $1.412 billion derived from PHS Evaluation financing... Additional sources: https://www.nih.gov/about-nih/organization/budget | https://officeofbudget.od.nih.gov/
.
64.
Bentley et al. NIH spending on clinical trials: 3.3%.
Bentley et al. https://pmc.ncbi.nlm.nih.gov/articles/PMC10349341/ (2023)
NIH spent $8.1 billion on clinical trials for approved drugs (2010-2019), representing 3.3% of relevant NIH spending. Additional sources: https://pmc.ncbi.nlm.nih.gov/articles/PMC10349341/ | https://catalyst.harvard.edu/news/article/nih-spent-8-1b-for-phased-clinical-trials-of-drugs-approved-2010-19-10-of-reported-industry-spending/
.
65.
PMC. Standard medical research ROI ($20k-$100k/QALY).
PMC: Cost-effectiveness Thresholds Used by Study Authors https://pmc.ncbi.nlm.nih.gov/articles/PMC10114019/ (1990)
Typical cost-effectiveness thresholds for medical interventions in rich countries range from $50,000 to $150,000 per QALY. The Institute for Clinical and Economic Review (ICER) uses a $100,000-$150,000/QALY threshold for value-based pricing. Between 1990-2021, authors increasingly cited $100,000 (47% by 2020-21) or $150,000 (24% by 2020-21) per QALY as benchmarks for cost-effectiveness. Additional sources: https://pmc.ncbi.nlm.nih.gov/articles/PMC10114019/ | https://icer.org/our-approach/methods-process/cost-effectiveness-the-qaly-and-the-evlyg/
.
66.
Institute, M. RECOVERY trial 82× cost reduction.
Manhattan Institute: Slow Costly Trials https://manhattan.institute/article/slow-costly-clinical-trials-drag-down-biomedical-breakthroughs RECOVERY trial: $500 per patient ($20M for 48,000 patients = $417/patient) Typical clinical trial: $41,000 median per-patient cost Cost reduction: 80-82× cheaper ($41,000 ÷ $500 ≈ 82×) Efficiency: $50 per patient per answer (10 therapeutics tested, 4 effective) Dexamethasone estimated to save >630,000 lives Additional sources: https://manhattan.institute/article/slow-costly-clinical-trials-drag-down-biomedical-breakthroughs | https://pmc.ncbi.nlm.nih.gov/articles/PMC9293394/
.
67.
Trials. Patient willingness to participate in clinical trials.
Trials: Patients’ Willingness Survey https://trialsjournal.biomedcentral.com/articles/10.1186/s13063-015-1105-3 Recent surveys: 49-51% willingness (2020-2022) - dramatic drop from 85% (2019) during COVID-19 pandemic Cancer patients when approached: 88% consented to trials (Royal Marsden Hospital) Study type variation: 44.8% willing for drug trial, 76.2% for diagnostic study Top motivation: "Learning more about my health/medical condition" (67.4%) Top barrier: "Worry about experiencing side effects" (52.6%) Additional sources: https://trialsjournal.biomedcentral.com/articles/10.1186/s13063-015-1105-3 | https://www.appliedclinicaltrialsonline.com/view/industry-forced-to-rethink-patient-participation-in-trials | https://pmc.ncbi.nlm.nih.gov/articles/PMC7183682/
.
68.
CSDD, T. Cost of drug development.
Various estimates suggest $1.0 - $2.5 billion to bring a new drug from discovery through FDA approval, spread across 10 years. Tufts Center for the Study of Drug Development often cited for $1.0 - $2.6 billion/drug. Industry reports (IQVIA, Deloitte) also highlight $2+ billion figures.
69.
Value in Health. Average lifetime revenue per successful drug.
Value in Health: Sales Revenues for New Therapeutic Agents https://www.sciencedirect.com/science/article/pii/S1098301524027542 Study of 361 FDA-approved drugs from 1995-2014 (median follow-up 13.2 years): Mean lifetime revenue: $15.2 billion per drug Median lifetime revenue: $6.7 billion per drug Revenue after 5 years: $3.2 billion (mean) Revenue after 10 years: $9.5 billion (mean) Revenue after 15 years: $19.2 billion (mean) Distribution highly skewed: top 25 drugs (7%) accounted for 38% of total revenue ($2.1T of $5.5T) Additional sources: https://www.sciencedirect.com/science/article/pii/S1098301524027542
.
70.
Lichtenberg, F. R.
How many life-years have new drugs saved? A three-way fixed-effects analysis of 66 diseases in 27 countries, 2000-2013.
International Health 11, 403–416 (2019)
Using 3-way fixed-effects methodology (disease-country-year) across 66 diseases in 22 countries, this study estimates that drugs launched after 1981 saved 148.7 million life-years in 2013 alone. The regression coefficients for drug launches 0-11 years prior (beta=-0.031, SE=0.008) and 12+ years prior (beta=-0.057, SE=0.013) on years of life lost are highly significant (p<0.0001). Confidence interval for life-years saved: 79.4M-239.8M (95 percent CI) based on propagated standard errors from Table 2.
71.
Deloitte. Pharmaceutical r&d return on investment (ROI).
Deloitte: Measuring Pharmaceutical Innovation 2025 https://www.deloitte.com/ch/en/Industries/life-sciences-health-care/research/measuring-return-from-pharmaceutical-innovation.html (2025)
Deloitte’s annual study of top 20 pharma companies by R&D spend (2010-2024): 2024 ROI: 5.9% (second year of growth after decade of decline) 2023 ROI: 4.3% (estimated from trend) 2022 ROI: 1.2% (historic low since study began, 13-year low) 2021 ROI: 6.8% (record high, inflated by COVID-19 vaccines/treatments) Long-term trend: Declining for over a decade before 2023 recovery Average R&D cost per asset: $2.3B (2022), $2.23B (2024) These returns (1.2-5.9% range) fall far below typical corporate ROI targets (15-20%) Additional sources: https://www.deloitte.com/ch/en/Industries/life-sciences-health-care/research/measuring-return-from-pharmaceutical-innovation.html | https://www.prnewswire.com/news-releases/deloittes-13th-annual-pharmaceutical-innovation-report-pharma-rd-return-on-investment-falls-in-post-pandemic-market-301738807.html | https://hitconsultant.net/2023/02/16/pharma-rd-roi-falls-to-lowest-level-in-13-years/
.
72.
Nature Reviews Drug Discovery. Drug trial success rate from phase i to approval.
Nature Reviews Drug Discovery: Clinical Success Rates https://www.nature.com/articles/nrd.2016.136 (2016)
Overall Phase I to approval: 10-12.8% (conventional wisdom 10%, studies show 12.8%) Recent decline: Average LOA now 6.7% for Phase I (2014-2023 data) Leading pharma companies: 14.3% average LOA (range 8-23%) Varies by therapeutic area: Oncology 3.4%, CNS/cardiovascular lowest at Phase III Phase-specific success: Phase I 47-54%, Phase II 28-34%, Phase III 55-70% Note: 12% figure accurate for historical average. Recent data shows decline to 6.7%, with Phase II as primary attrition point (28% success) Additional sources: https://www.nature.com/articles/nrd.2016.136 | https://pmc.ncbi.nlm.nih.gov/articles/PMC6409418/ | https://academic.oup.com/biostatistics/article/20/2/273/4817524
.
73.
SofproMed. Phase 3 cost per trial range.
SofproMed https://www.sofpromed.com/how-much-does-a-clinical-trial-cost Phase 3 clinical trials cost between $20 million and $282 million per trial, with significant variation by therapeutic area and trial complexity. Additional sources: https://www.sofpromed.com/how-much-does-a-clinical-trial-cost | https://www.cbo.gov/publication/57126
.
74.
Ramsberg J, P. R. Pragmatic trial cost per patient (median $97).
Learning Health Systems https://pmc.ncbi.nlm.nih.gov/articles/PMC6508852/ (2018)
Meta-analysis of 108 embedded pragmatic clinical trials (2006-2016). The median cost per patient was $97 (IQR $19–$478), based on 2015 dollars. 25% of trials cost <$19/patient; 10 trials exceeded $1,000/patient. U.S. studies median $187 vs non-U.S. median $27. Additional sources: https://pmc.ncbi.nlm.nih.gov/articles/PMC6508852/
.
75.
WHO. Polio vaccination ROI.
WHO https://www.who.int/news-room/feature-stories/detail/sustaining-polio-investments-offers-a-high-return (2019)
For every dollar spent, the return on investment is nearly US$ 39." Total investment cost of US$ 7.5 billion generates projected economic and social benefits of US$ 289.2 billion from sustaining polio assets and integrating them into expanded immunization, surveillance and emergency response programmes across 8 priority countries (Afghanistan, Iraq, Libya, Pakistan, Somalia, Sudan, Syria, Yemen). Additional sources: https://www.who.int/news-room/feature-stories/detail/sustaining-polio-investments-offers-a-high-return
.
76.
ICRC. International campaign to ban landmines (ICBL) - ottawa treaty (1997).
ICRC https://www.icrc.org/en/doc/resources/documents/article/other/57jpjn.htm (1997)
ICBL: Founded 1992 by 6 NGOs (Handicap International, Human Rights Watch, Medico International, Mines Advisory Group, Physicians for Human Rights, Vietnam Veterans of America Foundation) Started with ONE staff member: Jody Williams as founding coordinator Grew to 1,000+ organizations in 60 countries by 1997 Ottawa Process: 14 months (October 1996 - December 1997) Convention signed by 122 states on December 3, 1997; entered into force March 1, 1999 Achievement: Nobel Peace Prize 1997 (shared by ICBL and Jody Williams) Government funding context: Canada established $100M CAD Canadian Landmine Fund over 10 years (1997); International donors provided $169M in 1997 for mine action (up from $100M in 1996) Additional sources: https://www.icrc.org/en/doc/resources/documents/article/other/57jpjn.htm | https://en.wikipedia.org/wiki/International_Campaign_to_Ban_Landmines | https://www.nobelprize.org/prizes/peace/1997/summary/ | https://un.org/press/en/1999/19990520.MINES.BRF.html | https://www.the-monitor.org/en-gb/reports/2003/landmine-monitor-2003/mine-action-funding.aspx
.
77.
OpenSecrets.
Revolving door: Former members of congress. (2024)
388 former members of Congress are registered as lobbyists. Nearly 5,400 former congressional staffers have left Capitol Hill to become federal lobbyists in the past 10 years. Additional sources: https://www.opensecrets.org/revolving-door
.
78.
Kinch, M. S. & Griesenauer, R. H.
Lost medicines: A longer view of the pharmaceutical industry with the potential to reinvigorate discovery.
Drug Discovery Today 24, 875–880 (2019)
Research identified 1,600+ medicines available in 1962. The 1950s represented industry high-water mark with >30 new products in five of ten years; this rate would not be replicated until late 1990s. More than half (880) of these medicines were lost following implementation of Kefauver-Harris Amendment. The peak of 1962 would not be seen again until early 21st century. By 2016 number of organizations actively involved in R&D at level not seen since 1914.
79.
Wikipedia. US military spending reduction after WWII.
Wikipedia https://en.wikipedia.org/wiki/Demobilization_of_United_States_Armed_Forces_after_World_War_II (2020)
Peaking at over $81 billion in 1945, the U.S. military budget plummeted to approximately $13 billion by 1948, representing an 84% decrease. The number of personnel was reduced almost 90%, from more than 12 million to about 1.5 million between mid-1945 and mid-1947. Defense spending exceeded 41 percent of GDP in 1945. After World War II, the US reduced military spending to 7.2 percent of GDP by 1948. Defense spending doubled from the 1948 low to 15 percent at the height of the Korean War in 1953. Additional sources: https://en.wikipedia.org/wiki/Demobilization_of_United_States_Armed_Forces_after_World_War_II | https://www.americanprogress.org/article/a-historical-perspective-on-military-budgets/ | https://www.stlouisfed.org/on-the-economy/2020/february/war-highest-military-spending-measured | https://www.usgovernmentspending.com/defense_spending_history
.
80.
Baily, M. N. Pre-1962 drug development costs (baily 1972).
Baily (1972) https://samizdathealth.org/wp-content/uploads/2020/12/hlthaff.1.2.6.pdf (1972)
Pre-1962: Average cost per new chemical entity (NCE) was $6.5 million (1980 dollars) Inflation-adjusted to 2024 dollars: $6.5M (1980) ≈ $22.5M (2024), using CPI multiplier of 3.46× Real cost increase (inflation-adjusted): $22.5M (pre-1962) → $2,600M (2024) = 116× increase Note: This represents the most comprehensive academic estimate of pre-1962 drug development costs based on empirical industry data Additional sources: https://samizdathealth.org/wp-content/uploads/2020/12/hlthaff.1.2.6.pdf
.
81.
Think by Numbers. Pre-1962 physician-led clinical trials.
Think by Numbers: How Many Lives Does FDA Save? https://thinkbynumbers.org/health/how-many-net-lives-does-the-fda-save/ (1966)
Pre-1962: Physicians could report real-world evidence directly 1962 Drug Amendments replaced "premarket notification" with "premarket approval", requiring extensive efficacy testing Impact: New regulatory clampdown reduced new treatment production by 70%; lifespan growth declined from 4 years/decade to 2 years/decade Drug Efficacy Study Implementation (DESI): NAS/NRC evaluated 3,400+ drugs approved 1938-1962 for safety only; reviewed >3,000 products, >16,000 therapeutic claims FDA has had authority to accept real-world evidence since 1962, clarified by 21st Century Cures Act (2016) Note: Specific "144,000 physicians" figure not verified in sources Additional sources: https://thinkbynumbers.org/health/how-many-net-lives-does-the-fda-save/ | https://www.fda.gov/drugs/enforcement-activities-fda/drug-efficacy-study-implementation-desi | http://www.nasonline.org/about-nas/history/archives/collections/des-1966-1969-1.html
.
82.
GAO. 95% of diseases have 0 FDA-approved treatments.
GAO https://www.gao.gov/products/gao-25-106774 (2025)
95% of diseases have no treatment Additional sources: https://www.gao.gov/products/gao-25-106774 | https://globalgenes.org/rare-disease-facts/
.
84.
al., N. E. Á. et. RECOVERY trial global lives saved ( 1 million).
NHS England: 1 Million Lives Saved https://www.england.nhs.uk/2021/03/covid-treatment-developed-in-the-nhs-saves-a-million-lives/ (2021)
Dexamethasone saved 1 million lives worldwide (NHS England estimate, March 2021, 9 months after discovery). UK alone: 22,000 lives saved. Methodology: Águas et al. Nature Communications 2021 estimated 650,000 lives (range: 240,000-1,400,000) for July-December 2020 alone, based on RECOVERY trial mortality reductions (36% for ventilated, 18% for oxygen-only patients) applied to global COVID hospitalizations. June 2020 announcement: Dexamethasone reduced deaths by up to 1/3 (ventilated patients), 1/5 (oxygen patients). Impact immediate: Adopted into standard care globally within hours of announcement. Additional sources: https://www.england.nhs.uk/2021/03/covid-treatment-developed-in-the-nhs-saves-a-million-lives/ | https://www.nature.com/articles/s41467-021-21134-2 | https://pharmaceutical-journal.com/article/news/steroid-has-saved-the-lives-of-one-million-covid-19-patients-worldwide-figures-show | https://www.recoverytrial.net/news/recovery-trial-celebrates-two-year-anniversary-of-life-saving-dexamethasone-result
.
85.
Museum, N. S. 11. M. &.
September 11 attack facts. (2024)
2,977 people were killed in the September 11, 2001 attacks: 2,753 at the World Trade Center, 184 at the Pentagon, and 40 passengers and crew on United Flight 93 in Shanksville, Pennsylvania.
86.
World Bank. World bank singapore economic data.
World Bank https://data.worldbank.org/country/singapore (2024)
Singapore GDP per capita (2023): $82,000 - among highest in the world Government spending: 15% of GDP (vs US 38%) Life expectancy: 84.1 years (vs US 77.5 years) Singapore demonstrates that low government spending can coexist with excellent outcomes Additional sources: https://data.worldbank.org/country/singapore
.
87.
Fund, I. M.
IMF singapore government spending data. (2024)
Singapore government spending is approximately 15% of GDP This is 23 percentage points lower than the United States (38%) Despite lower spending, Singapore achieves excellent outcomes: - Life expectancy: 84.1 years (vs US 77.5) - Low crime, world-class infrastructure, AAA credit rating Additional sources: https://www.imf.org/en/Countries/SGP
.
88.
World Health Organization.
WHO life expectancy data by country. (2024)
Life expectancy at birth varies significantly among developed nations: Switzerland: 84.0 years (2023) Singapore: 84.1 years (2023) Japan: 84.3 years (2023) United States: 77.5 years (2023) - 6.5 years below Switzerland, Singapore Global average: 73 years Note: US spends more per capita on healthcare than any other nation, yet achieves lower life expectancy Additional sources: https://www.who.int/data/gho/data/themes/mortality-and-global-health-estimates/ghe-life-expectancy-and-healthy-life-expectancy
.
90.
PMC. Contribution of smoking reduction to life expectancy gains.
PMC: Benefits Smoking Cessation Longevity https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1447499/ (2012)
Population-level: Up to 14% (9% men, 14% women) of total life expectancy gain since 1960 due to tobacco control efforts Individual cessation benefits: Quitting at age 35 adds 6.9-8.5 years (men), 6.1-7.7 years (women) vs continuing smokers By cessation age: Age 25-34 = 10 years gained; age 35-44 = 9 years; age 45-54 = 6 years; age 65 = 2.0 years (men), 3.7 years (women) Cessation before age 40: Reduces death risk by 90% Long-term cessation: 10+ years yields survival comparable to never smokers, averts 10 years of life lost Recent cessation: <3 years averts 5 years of life lost Additional sources: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1447499/ | https://www.cdc.gov/pcd/issues/2012/11_0295.htm | https://www.ajpmonline.org/article/S0749-3797(24)00217-4/fulltext | https://www.nejm.org/doi/full/10.1056/NEJMsa1211128
.
91.
ICER. Value per QALY (standard economic value).
ICER https://icer.org/wp-content/uploads/2024/02/Reference-Case-4.3.25.pdf (2024)
Standard economic value per QALY: $100,000–$150,000. This is the US and global standard willingness-to-pay threshold for interventions that add costs. Dominant interventions (those that save money while improving health) are favorable regardless of this threshold. Additional sources: https://icer.org/wp-content/uploads/2024/02/Reference-Case-4.3.25.pdf
.
92.
GAO. Annual cost of u.s. Sugar subsidies.
GAO: Sugar Program https://www.gao.gov/products/gao-24-106144 Consumer costs: $2.5-3.5 billion per year (GAO estimate) Net economic cost: $1 billion per year 2022: US consumers paid 2X world price for sugar Program costs $3-4 billion/year but no federal budget impact (costs passed directly to consumers via higher prices) Employment impact: 10,000-20,000 manufacturing jobs lost annually in sugar-reliant industries (confectionery, etc.) Multiple studies confirm: Sweetener Users Association ($2.9-3.5B), AEI ($2.4B consumer cost), Beghin & Elobeid ($2.9-3.5B consumer surplus) Additional sources: https://www.gao.gov/products/gao-24-106144 | https://www.heritage.org/agriculture/report/the-us-sugar-program-bad-consumers-bad-agriculture-and-bad-america | https://www.aei.org/articles/the-u-s-spends-4-billion-a-year-subsidizing-stalinist-style-domestic-sugar-production/
.
93.
World Bank. Swiss military budget as percentage of GDP.
World Bank: Military Expenditure https://data.worldbank.org/indicator/MS.MIL.XPND.GD.ZS?locations=CH 2023: 0.70272% of GDP (World Bank) 2024: CHF 5.95 billion official military spending When including militia system costs: 1% GDP (CHF 8.75B) Comparison: Near bottom in Europe; only Ireland, Malta, Moldova spend less (excluding microstates with no armies) Additional sources: https://data.worldbank.org/indicator/MS.MIL.XPND.GD.ZS?locations=CH | https://www.avenir-suisse.ch/en/blog-defence-spending-switzerland-is-in-better-shape-than-it-seems/ | https://tradingeconomics.com/switzerland/military-expenditure-percent-of-gdp-wb-data.html
.
94.
World Bank. Switzerland vs. US GDP per capita comparison.
World Bank: Switzerland GDP Per Capita https://data.worldbank.org/indicator/NY.GDP.PCAP.CD?locations=CH 2024 GDP per capita (PPP-adjusted): Switzerland $93,819 vs United States $75,492 Switzerland’s GDP per capita 24% higher than US when adjusted for purchasing power parity Nominal 2024: Switzerland $103,670 vs US $85,810 Additional sources: https://data.worldbank.org/indicator/NY.GDP.PCAP.CD?locations=CH | https://tradingeconomics.com/switzerland/gdp-per-capita-ppp | https://www.theglobaleconomy.com/USA/gdp_per_capita_ppp/
.
95.
OECD.
OECD government spending as percentage of GDP. (2024)
OECD government spending data shows significant variation among developed nations: United States: 38.0% of GDP (2023) Switzerland: 35.0% of GDP - 3 percentage points lower than US Singapore: 15.0% of GDP - 23 percentage points lower than US (per IMF data) OECD average: approximately 40% of GDP Additional sources: https://data.oecd.org/gga/general-government-spending.htm
.
96.
OECD.
OECD median household income comparison. (2024)
Median household disposable income varies significantly across OECD nations: United States: $77,500 (2023) Switzerland: $55,000 PPP-adjusted (lower nominal but comparable purchasing power) Singapore: $75,000 PPP-adjusted Additional sources: https://data.oecd.org/hha/household-disposable-income.htm
.
97.
Institute, C. Chance of dying from terrorism statistic.
Cato Institute: Terrorism and Immigration Risk Analysis https://www.cato.org/policy-analysis/terrorism-immigration-risk-analysis Chance of American dying in foreign-born terrorist attack: 1 in 3.6 million per year (1975-2015) Including 9/11 deaths; annual murder rate is 253x higher than terrorism death rate More likely to die from lightning strike than foreign terrorism Note: Comprehensive 41-year study shows terrorism risk is extremely low compared to everyday dangers Additional sources: https://www.cato.org/policy-analysis/terrorism-immigration-risk-analysis | https://www.nbcnews.com/news/us-news/you-re-more-likely-die-choking-be-killed-foreign-terrorists-n715141
.
98.
Wikipedia. Thalidomide scandal: Worldwide cases and mortality.
Wikipedia https://en.wikipedia.org/wiki/Thalidomide_scandal The total number of embryos affected by the use of thalidomide during pregnancy is estimated at 10,000, of whom about 40% died around the time of birth. More than 10,000 children in 46 countries were born with deformities such as phocomelia. Additional sources: https://en.wikipedia.org/wiki/Thalidomide_scandal
.
99.
One, P. Health and quality of life of thalidomide survivors as they age.
PLOS One https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0210222 (2019)
Study of thalidomide survivors documenting ongoing disability impacts, quality of life, and long-term health outcomes. Survivors (now in their 60s) continue to experience significant disability from limb deformities, organ damage, and other effects. Additional sources: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0210222
.
101.
FDA Study via NCBI. Trial costs, FDA study.
FDA Study via NCBI https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6248200/ Overall, the 138 clinical trials had an estimated median (IQR) cost of $19.0 million ($12.2 million-$33.1 million)... The clinical trials cost a median (IQR) of $41,117 ($31,802-$82,362) per patient. Additional sources: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6248200/
.
102.
Diseases, G. 2019. & Collaborators, I.
Global burden of disease study 2019: Disability weights.
The Lancet 396, 1204–1222 (2020)
Disability weights for 235 health states used in Global Burden of Disease calculations. Weights range from 0 (perfect health) to 1 (death equivalent). Chronic conditions like diabetes (0.05-0.35), COPD (0.04-0.41), depression (0.15-0.66), and cardiovascular disease (0.04-0.57) show substantial variation by severity. Treatment typically reduces disability weights by 50-80 percent for manageable chronic conditions.
103.
WHO. Annual global economic burden of alzheimer’s and other dementias.
WHO: Dementia Fact Sheet https://www.who.int/news-room/fact-sheets/detail/dementia (2019)
Global cost: $1.3 trillion (2019 WHO-commissioned study) 50% from informal caregivers (family/friends, 5 hrs/day) 74% of costs in high-income countries despite 61% of patients in LMICs $818B (2010) → $1T (2018) → $1.3T (2019) - rapid growth Note: Costs increased 35% from 2010-2015 alone. Informal care represents massive hidden economic burden Additional sources: https://www.who.int/news-room/fact-sheets/detail/dementia | https://alz-journals.onlinelibrary.wiley.com/doi/10.1002/alz.12901
.
104.
Oncology, J. Annual global economic burden of cancer.
JAMA Oncology: Global Cost 2020-2050 https://jamanetwork.com/journals/jamaoncology/fullarticle/2801798 (2020)
2020-2050 projection: $25.2 trillion total ($840B/year average) 2010 annual cost: $1.16 trillion (direct costs only) Recent estimate: $3 trillion/year (all costs included) Top 5 cancers: lung (15.4%), colon/rectum (10.9%), breast (7.7%), liver (6.5%), leukemia (6.3%) Note: China/US account for 45% of global burden; 75% of deaths in LMICs but only 50.0% of economic cost Additional sources: https://jamanetwork.com/journals/jamaoncology/fullarticle/2801798 | https://www.nature.com/articles/d41586-023-00634-9
.
106.
Care, D. Annual global economic burden of diabetes.
Diabetes Care: Global Economic Burden https://diabetesjournals.org/care/article/41/5/963/36522/Global-Economic-Burden-of-Diabetes-in-Adults 2015: $1.3 trillion (1.8% of global GDP) 2030 projections: $2.1T-2.5T depending on scenario IDF health expenditure: $760B (2019) → $845B (2045 projected) 2/3 direct medical costs ($857B), 1/3 indirect costs (lost productivity) Note: Costs growing rapidly; expected to exceed $2T by 2030 Additional sources: https://diabetesjournals.org/care/article/41/5/963/36522/Global-Economic-Burden-of-Diabetes-in-Adults | https://doi.org/10.1016/S2213-8587(17)30097-9
.
108.
World Bank, B. of E. A. US GDP 2024 ($28.78 trillion).
World Bank https://data.worldbank.org/indicator/NY.GDP.MKTP.CD?locations=US (2024)
US GDP reached $28.78 trillion in 2024, representing approximately 26% of global GDP. Additional sources: https://data.worldbank.org/indicator/NY.GDP.MKTP.CD?locations=US | https://www.bea.gov/news/2024/gross-domestic-product-fourth-quarter-and-year-2024-advance-estimate
.
109.
Group, E. W. US farm subsidy database and analysis.
Environmental Working Group https://farm.ewg.org/ (2024)
US agricultural subsidies total approximately $30 billion annually, but create much larger economic distortions. Top 10% of farms receive 78% of subsidies, benefits concentrated in commodity crops (corn, soy, wheat, cotton), environmental damage from monoculture incentivized, and overall deadweight loss estimated at $50-120 billion annually. Additional sources: https://farm.ewg.org/ | https://www.ers.usda.gov/topics/farm-economy/farm-sector-income-finances/government-payments-the-safety-net/
.
110.
Alliance, D. P.
The drug war by the numbers. (2021)
Since 1971, the war on drugs has cost the United States an estimated $1 trillion in enforcement. The federal drug control budget was $41 billion in 2022. Mass incarceration costs the U.S. at least $182 billion every year, with over $450 billion spent to incarcerate individuals on drug charges in federal prisons.
111.
Fund, I. M.
IMF fossil fuel subsidies data: 2023 update. (2023)
Globally, fossil fuel subsidies were $7 trillion in 2022 or 7.1 percent of GDP. The United States subsidies totaled $649 billion. Underpricing for local air pollution costs and climate damages are the largest contributor, accounting for about 30 percent each.
112.
Papanicolas, I. et al. Health care spending in the united states and other high-income countries.
Papanicolas et al. https://jamanetwork.com/journals/jama/article-abstract/2674671 (2018)
The US spent approximately twice as much as other high-income countries on medical care (mean per capita: $9,892 vs $5,289), with similar utilization but much higher prices. Administrative costs accounted for 8% of US spending vs 1-3% in other countries. US spending on pharmaceuticals was $1,443 per capita vs $749 elsewhere. Despite spending more, US health outcomes are not better. Additional sources: https://jamanetwork.com/journals/jama/article-abstract/2674671
.
113.
Hsieh, C.-T. & Moretti, E. Housing constraints and spatial misallocation.
American Economic Journal: Macroeconomics https://www.aeaweb.org/articles?id=10.1257/mac.20170388 (2019)
We quantify the amount of spatial misallocation of labor across US cities and its aggregate costs. Tight land-use restrictions in high-productivity cities like New York, San Francisco, and Boston lowered aggregate US growth by 36% from 1964 to 2009. Local constraints on housing supply have had enormous effects on the national economy. Additional sources: https://www.aeaweb.org/articles?id=10.1257/mac.20170388
.
115.
Foundation, T. Tax compliance costs the US economy $546 billion annually.
https://taxfoundation.org/data/all/federal/irs-tax-compliance-costs/ (2024)
Americans will spend over 7.9 billion hours complying with IRS tax filing and reporting requirements in 2024. This costs the economy roughly $413 billion in lost productivity. In addition, the IRS estimates that Americans spend roughly $133 billion annually in out-of-pocket costs, bringing the total compliance costs to $546 billion, or nearly 2 percent of GDP.
116.
Cook, C., Cole, G., Asaria, P., Jabbour, R. & Francis, D. P. Annual global economic burden of heart disease.
International Journal of Cardiology https://www.internationaljournalofcardiology.com/article/S0167-5273(13)02238-9/abstract (2014)
Heart failure alone: $108 billion/year (2012 global analysis, 197 countries) US CVD: $555B (2016) → projected $1.8T by 2050 LMICs total CVD loss: $3.7T cumulative (2011-2015, 5-year period) CVD is costliest disease category in most developed nations Note: No single $2.1T global figure found; estimates vary widely by scope and year Additional sources: https://www.ahajournals.org/doi/10.1161/CIR.0000000000001258
.
117.
Source: US Life Expectancy FDA Budget 1543-2019 CSV.
US life expectancy growth 1880-1960: 3.82 years per decade. (2019)
Pre-1962: 3.82 years/decade Post-1962: 1.54 years/decade Reduction: 60% decline in life expectancy growth rate Additional sources: https://ourworldindata.org/life-expectancy | https://www.mortality.org/ | https://www.cdc.gov/nchs/nvss/mortality_tables.htm
.
118.
Source: US Life Expectancy FDA Budget 1543-2019 CSV.
Post-1962 slowdown in life expectancy gains. (2019)
Pre-1962 (1880-1960): 3.82 years/decade Post-1962 (1962-2019): 1.54 years/decade Reduction: 60% decline Temporal correlation: Slowdown occurred immediately after 1962 Kefauver-Harris Amendment Additional sources: https://ourworldindata.org/life-expectancy | https://www.mortality.org/ | https://www.cdc.gov/nchs/nvss/mortality_tables.htm
.
119.
Centers for Disease Control and Prevention.
US life expectancy 2023. (2024)
US life expectancy at birth was 77.5 years in 2023 Male life expectancy: 74.8 years Female life expectancy: 80.2 years This is 6-7 years lower than peer developed nations despite higher healthcare spending Additional sources: https://www.cdc.gov/nchs/fastats/life-expectancy.htm
.
120.
Bureau, U. C.
US median household income 2023. (2024)
US median household income was $77,500 in 2023 Real median household income declined 0.8% from 2022 Gini index: 0.467 (income inequality measure) Additional sources: https://www.census.gov/library/publications/2024/demo/p60-282.html
.
121.
Statista. US military budget as percentage of GDP.
Statista https://www.statista.com/statistics/262742/countries-with-the-highest-military-spending/ (2024)
U.S. military spending amounted to 3.5% of GDP in 2024. In 2024, the U.S. spent nearly $1 trillion on its military budget, equal to 3.4% of GDP. Additional sources: https://www.statista.com/statistics/262742/countries-with-the-highest-military-spending/ | https://www.sipri.org/sites/default/files/2025-04/2504_fs_milex_2024.pdf
.
122.
Bureau, U. C. Number of registered or eligible voters in the u.s.
US Census Bureau https://www.census.gov/newsroom/press-releases/2025/2024-presidential-election-voting-registration-tables.html (2024)
73.6% (or 174 million people) of the citizen voting-age population was registered to vote in 2024 (Census Bureau). More than 211 million citizens were active registered voters (86.6% of citizen voting age population) according to the Election Assistance Commission. Additional sources: https://www.census.gov/newsroom/press-releases/2025/2024-presidential-election-voting-registration-tables.html | https://www.eac.gov/news/2025/06/30/us-election-assistance-commission-releases-2024-election-administration-and-voting
.
123.
Senate, U. S. Treaties.
U.S. Senate https://www.senate.gov/about/powers-procedures/treaties.htm The Constitution provides that the president ’shall have Power, by and with the Advice and Consent of the Senate, to make Treaties, provided two-thirds of the Senators present concur’ (Article II, section 2). Treaties are formal agreements with foreign nations that require two-thirds Senate approval. 67 senators (two-thirds of 100) must vote to ratify a treaty for it to take effect. Additional sources: https://www.senate.gov/about/powers-procedures/treaties.htm
.
124.
Commission, F. E.
Statistical summary of 24-month campaign activity of the 2023-2024 election cycle. (2023)
Presidential candidates raised $2 billion; House and Senate candidates raised $3.8 billion and spent $3.7 billion; PACs raised $15.7 billion and spent $15.5 billion. Total federal campaign spending approximately $20 billion. Additional sources: https://www.fec.gov/updates/statistical-summary-of-24-month-campaign-activity-of-the-2023-2024-election-cycle/
.
125.
OpenSecrets.
Federal lobbying hit record $4.4 billion in 2024. (2024)
Total federal lobbying reached record $4.4 billion in 2024. The $150 million increase in lobbying continues an upward trend that began in 2016. Additional sources: https://www.opensecrets.org/news/2025/02/federal-lobbying-set-new-record-in-2024/
.
126.
Hutchinson & Kirk.
Valley of death in drug development. (2011)
The overall failure rate of drugs that passed into Phase 1 trials to final approval is 90%. This lack of translation from promising preclinical findings to success in human trials is known as the "valley of death." Estimated 30-50% of promising compounds never proceed to Phase 2/3 trials primarily due to funding barriers rather than scientific failure. The late-stage attrition rate for oncology drugs is as high as 70% in Phase II and 59% in Phase III trials.
127.
DOT. DOT value of statistical life ($13.6M).
DOT: VSL Guidance 2024 https://www.transportation.gov/office-policy/transportation-policy/revised-departmental-guidance-on-valuation-of-a-statistical-life-in-economic-analysis (2024)
Current VSL (2024): $13.7 million (updated from $13.6M) Used in cost-benefit analyses for transportation regulations and infrastructure Methodology updated in 2013 guidance, adjusted annually for inflation and real income VSL represents aggregate willingness to pay for safety improvements that reduce fatalities by one Note: DOT has published VSL guidance periodically since 1993. Current $13.7M reflects 2024 inflation/income adjustments Additional sources: https://www.transportation.gov/office-policy/transportation-policy/revised-departmental-guidance-on-valuation-of-a-statistical-life-in-economic-analysis | https://www.transportation.gov/regulations/economic-values-used-in-analysis
.
128.
ONE, P. Cost per DALY for vitamin a supplementation.
PLOS ONE: Cost-effectiveness of "Golden Mustard" for Treating Vitamin A Deficiency in India (2010) https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0012046 (2010)
India: $23-$50 per DALY averted (least costly intervention, $1,000-$6,100 per death averted) Sub-Saharan Africa (2022): $220-$860 per DALY (Burkina Faso: $220, Kenya: $550, Nigeria: $860) WHO estimates for Africa: $40 per DALY for fortification, $255 for supplementation Uganda fortification: $18-$82 per DALY (oil: $18, sugar: $82) Note: Wide variation reflects differences in baseline VAD prevalence, coverage levels, and whether intervention is supplementation or fortification Additional sources: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0012046 | https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0266495
.
130.
PMC. Cost-effectiveness threshold ($50,000/QALY).
PMC https://pmc.ncbi.nlm.nih.gov/articles/PMC5193154/ The $50,000/QALY threshold is widely used in US health economics literature, originating from dialysis cost benchmarks in the 1980s. In US cost-utility analyses, 77.5% of authors use either $50,000 or $100,000 per QALY as reference points. Most successful health programs cost $3,000-10,000 per QALY. WHO-CHOICE uses GDP per capita multiples (1× GDP/capita = "very cost-effective", 3× GDP/capita = "cost-effective"), which for the US ( $70,000 GDP/capita) translates to $70,000-$210,000/QALY thresholds. Additional sources: https://pmc.ncbi.nlm.nih.gov/articles/PMC5193154/ | https://pmc.ncbi.nlm.nih.gov/articles/PMC9278384/
.
131.
Institute, I. B. Chronic illness workforce productivity loss.
Integrated Benefits Institute 2024 https://www.ibiweb.org/resources/chronic-conditions-in-the-us-workforce-prevalence-trends-and-productivity-impacts (2024)
78.4% of U.S. employees have at least one chronic condition (7% increase since 2021) 58% of employees report physical chronic health conditions 28% of all employees experience productivity loss due to chronic conditions Average productivity loss: $4,798 per employee per year Employees with 3+ chronic conditions miss 7.8 days annually vs 2.2 days for those without Note: 28% productivity loss translates to roughly 11 hours per week (28% of 40-hour workweek) Additional sources: https://www.ibiweb.org/resources/chronic-conditions-in-the-us-workforce-prevalence-trends-and-productivity-impacts | https://www.onemedical.com/mediacenter/study-finds-more-than-half-of-employees-are-living-with-chronic-conditions-including-1-in-3-gen-z-and-millennial-employees/ | https://debeaumont.org/news/2025/poll-the-toll-of-chronic-health-conditions-on-employees-and-workplaces/
.
132.
Ramsberg J, P. R. Opportunities and barriers for pragmatic embedded trials: Triumphs and tribulations.
Harvard Medical School/Harvard Pilgrim Health Care Institute https://pmc.ncbi.nlm.nih.gov/articles/PMC6508852/ (2018)
Meta-analysis of 108 embedded pragmatic clinical trials (2006-2016). The median cost per patient was $97 (mean $478) across all trials reviewed. 25% of studies cost less than $19 per patient. US studies had higher median costs ($187 vs $27 non-US). Registry-based trials were less expensive than EHR-based trials. Traditional RCT comparison: $16,600/patient (Berndt & Cockburn 2014). The 108 trials had median enrollment of 5,540 patients with broad eligibility criteria. 81% used cluster randomization. Trials spanned 15 countries, infectious diseases (25%), cardiovascular (18%), diabetes (12%). Additional sources: https://pmc.ncbi.nlm.nih.gov/articles/PMC6508852/
.
133.
AllTrials. Publication rate of clinical trial results.
AllTrials: Half of Trials Unreported https://www.alltrials.net/news/half-of-all-trials-unreported/ (2013)
50.0% of clinical trials never publish results (NHS-funded systematic review, 2010) Schmucker et al (2014): 53% of trials published (analyzing 39 studies, >20,000 trials) Munch et al (2014): 46% of pain treatment trials published Chang et al (2015): 49% of high-risk cardiac device trials published Positive findings: 3X more likely to be published than negative results Antidepressant example: Published literature showed 94% positive trials; FDA analysis showed only 51% positive Additional sources: https://www.alltrials.net/news/half-of-all-trials-unreported/ | https://www.nature.com/articles/nature.2013.14286 | https://pmc.ncbi.nlm.nih.gov/articles/PMC8276556/
.
134.
al., S. et. FAERS adverse event underreporting rate.
PubMed: Empirical estimation of under-reporting in FAERS https://pubmed.ncbi.nlm.nih.gov/28447485/ (2017)
Empirical estimation: Average reporting rate approximately 6%, meaning 94% of adverse events are underreported Variability: 0.01% to 44% for statin events; 0.002% to >100% for biological drugs; 20% to >100% for narrow therapeutic index (NTI) drugs Selective reporting: Serious, unusual events more likely reported than mild or expected ones Newly marketed drugs: Higher reporting rates due to heightened awareness Older drugs: Events often under-reported Note: FAERS voluntary reporting system captures only "tip of the iceberg" of drug safety problems. Under-reporting introduces inherent biases and limitations in pharmacovigilance data Additional sources: https://pubmed.ncbi.nlm.nih.gov/28447485/ | https://pmc.ncbi.nlm.nih.gov/articles/PMC12393772/
.
135.
Graham, D. (FDA). |. L. Vioxx cardiovascular deaths (rofecoxib).
PMC: FDA incapable of protecting against another Vioxx https://pmc.ncbi.nlm.nih.gov/articles/PMC534432/ (2007)
Graham testimony (2004): 88,000-139,000 U.S. heart attacks/strokes from Vioxx; up to 55,000 deaths (40% fatality rate) Lancet study estimate: 88,000 Americans had heart attacks from Vioxx; 38,000 died FDA memo (2004): Vioxx contributed to 27,785 heart attacks and sudden cardiac deaths (1999-2003) High-dose Vioxx: Tripled risk of heart attacks and sudden cardiac death Prescriptions: 92.8 million U.S. prescriptions 1999-2003 Withdrawn: September 30, 2004 after APPROVE trial showed cardiovascular risks Note: Vioxx case demonstrates failure of passive post-market surveillance (FAERS) to detect safety signals in time. Voluntary reporting missed cardiovascular risks for years despite millions of prescriptions Additional sources: https://pmc.ncbi.nlm.nih.gov/articles/PMC534432/ | https://www.npr.org/2007/11/10/5470430/timeline-the-rise-and-fall-of-vioxx | https://www.thelancet.com/journals/lancet/article/PIIS0140-6736(05)67712-4/fulltext
.
136.
FDA. FDA sentinel initiative.
FDA: Sentinel Initiative https://www.fda.gov/safety/fdas-sentinel-initiative Launched: May 2008 in response to FDAAA 2007; transitioned to full system Feb 2016 Purpose: Active post-market risk identification and analysis (ARIA) for medical products Scale: World’s largest multisite distributed database for medical product safety; 128.7M members Data sources: Insurance claims, electronic health records, patient reports Privacy: Distributed data approach - data remains with owners, patient identifiers removed Structure (2019): 3 coordinating centers - Operations, Innovation, Community Building/Outreach Real-World Evidence: RWE Data Enterprise (RWE-DE) - 25.5M lives (21M commercial + 4.5M academic) 2008-2014: FDA mandated 657 studies under FDAAA authority Note: Major advancement in post-market surveillance. "Limited Transparency and Bureaucratic Constraints" may refer to challenges, but system represents significant FDA capability improvement Additional sources: https://www.fda.gov/safety/fdas-sentinel-initiative | https://pmc.ncbi.nlm.nih.gov/articles/PMC9667154/ | https://en.wikipedia.org/wiki/Sentinel_Initiative
.
139.
UNHCR. UNHCR forcibly displaced people 2023.
UNHCR https://www.unhcr.org/global-trends-report-2023 (2023)
At the end of 2023, 117.3 million people worldwide were forcibly displaced. Additional sources: https://www.unhcr.org/global-trends-report-2023
.
140.
News, O. U. RECOVERY trial summary quote.
Oxford University News https://www.ox.ac.uk/news/features/recovery-trial-two-years One trial. Over 47,000 participants. Nearly 200 hospital sites, across six countries. Ten results. Four effective COVID-19 treatments... Through discovering four treatments that effectively reduce deaths from COVID-19, it is certain that the study has saved thousands – if not millions – of lives worldwide. Additional sources: https://www.ox.ac.uk/news/features/recovery-trial-two-years
.
142.
FDA. FDA trial patient exclusion criteria.
FDA: Evaluating Inclusion & Exclusion Criteria https://www.fda.gov/media/134754/download Most frequent exclusions: Pregnancy, lactation/breastfeeding, renal/hepatic abnormalities, specific infectious diseases Pregnant/lactating women: >90% of trials exclude Older adults: 27% exclude based on age (arbitrary upper limits) Patients with organ dysfunction: Excluded due to adverse impact concerns from comorbidities/concomitant meds Multiple chronic conditions: Often exclusion criterion despite being common in target population Children/adolescents: Excluded due to ethical considerations High-risk patients: Prior malignancy history, active brain metastases, suboptimal hepatic/renal function, HIV+ FDA guidance: Working to broaden eligibility; "exclusions based on age alone rarely appropriate Note: Exclusion criteria often eliminate patients who would actually use the drug, reducing real-world applicability of trial results Additional sources: https://www.fda.gov/media/134754/download | https://www.sciencedirect.com/science/article/abs/pii/S1551714421002512 | https://ascopubs.org/doi/10.1200/EDBK_155880
.
144.
Bloom, C. I. J., Nicholas & Webb, M. Research productivity declining over time.
Bloom https://www.aeaweb.org/articles?id=10.1257/aer.20180338 (2020)
Research productivity is falling sharply everywhere we look. Averaging across industries, research productivity declines at a rate that averages about 5% per year. For example, the number of researchers required to achieve a constant level of Moore’s Law has risen by a factor of 18 since 1971. Note: This finding reflects innovation productivity in traditional research models; dFDA targets trial execution efficiency (cost per patient), not fundamental idea generation Additional sources: https://www.aeaweb.org/articles?id=10.1257/aer.20180338
.
145.
ICER. ICER QALY methodology and standards.
ICER https://icer.org/our-approach/methods-process/cost-effectiveness-the-qaly-and-the-evlyg/ (2024)
The quality-adjusted life year (QALY) is the academic standard for measuring how well all different kinds of medical treatments lengthen and/or improve patients’ lives, and therefore the metric has served as a fundamental component of cost-effectiveness analyses in the US and around the world for more than 30 years. ICER’s health benefit price benchmark (HBPB) will continue to be reported using the standard range from $100,000 to $150,000 per QALY and per evLYG. Additional sources: https://icer.org/our-approach/methods-process/cost-effectiveness-the-qaly-and-the-evlyg/ | https://icer.org/wp-content/uploads/2024/02/Reference-Case-4.3.25.pdf
.
146.
International, R. D. 300 million people with rare diseases globally.
Rare Diseases International: 300 Million Worldwide https://www.rarediseasesinternational.org/new-scientific-paper-confirms-300-million-people-living-with-a-rare-disease-worldwide/ (2019)
Conservative estimate: 300 million people (3.5-5.9% of world population of 7.5B) Range: 263-446 million people globally Based on Orphanet database analysis of 3,585 rare diseases Note: Excludes rare cancers and infectious diseases, so actual number likely higher Additional sources: https://www.rarediseasesinternational.org/new-scientific-paper-confirms-300-million-people-living-with-a-rare-disease-worldwide/ | https://sciencedaily.com/releases/2019/10/191024075007.htm | https://pmc.ncbi.nlm.nih.gov/articles/PMC9632971/
.
147.
Wikipedia. Journal of the american medical association (JAMA) founded in 1883.
Wikipedia: JAMA https://en.wikipedia.org/wiki/JAMA Founded: 1883 by American Medical Association Founding editor: Nathan Smith Davis Superseded: Transactions of the American Medical Association 1960: Obtained current title "JAMA: The Journal of the American Medical Association Evolution: Late 1800s resembled general journalism; 1910s-1920s "turndown era" began rejecting submissions based on quality; routine peer review instituted after WWII Current: Peer-reviewed medical journal published 48 times/year covering all aspects of biomedicine Additional sources: https://en.wikipedia.org/wiki/JAMA | https://jamanetwork.com/journals/jama/fullarticle/291201 | https://onlinebooks.library.upenn.edu/webbin/serial?id=jama
.
148.
FDA. FDA dr. Kelsey prevented widespread thalidomide birth defects in the US.
FDA: Frances Oldham Kelsey https://www.fda.gov/about-fda/fda-history-exhibits/frances-oldham-kelsey-medical-reviewer-famous-averting-public-health-tragedy Dr. Frances Kelsey (FDA reviewer) resisted pressure to approve thalidomide September 1960-November 1961 Worldwide: 8,000 infants born with missing/malformed limbs; 5,000-7,000 perished in utero United States: 17 confirmed phocomelia cases + 9 likely cases (vs. 8,000 worldwide) Kelsey insisted on hard evidence, refused to be browbeaten; repeatedly requested more information every 60 days Merrell complained to her bosses, calling her "petty bureaucrat" - she persisted Recognition: President’s Award for Distinguished Federal Civilian Service (JFK, 1962) Led to 1962 Kefauver-Harris Amendments requiring drugs prove both safety AND effectiveness Additional sources: https://www.fda.gov/about-fda/fda-history-exhibits/frances-oldham-kelsey-medical-reviewer-famous-averting-public-health-tragedy | https://www.uchicagomedicine.org/forefront/biological-sciences-articles/courageous-physician-scientist-saved-the-us-from-a-birth-defects-catastrophe | https://www.smithsonianmag.com/science-nature/woman-who-stood-between-america-and-epidemic-birth-defects-180963165/
.
151.
NIH. NIH centralized decision-making structure.
NIH Almanac https://www.nih.gov/about-nih/what-we-do/nih-almanac NIH structure: 27 Institutes and Centers, each with own research agenda Office of the Director: Sets policy, plans/manages/coordinates all NIH components Location: 9000 Rockville Pike, Bethesda, Maryland Total NIH employees: 20,000 Leadership structure: Director + 27 Institute/Center directors + division chiefs + council members Specific count of "key decision-makers" varies by definition; centralized funding decisions flow through Office of Director and IC leadership Additional sources: https://www.nih.gov/about-nih/what-we-do/nih-almanac | https://www.nih.gov/about-nih/what-we-do/nih-almanac/nih-organization
.
152.
Patsopoulos, N. A. Pragmatic vs. Explanatory trials.
Patsopoulos https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3181997/ (2011)
Pragmatic trials evaluate the effectiveness of interventions in real-life routine practice conditions, whereas explanatory trials determine the efficacy of interventions under ideal situations. Pragmatic trials produce results that can be generalized and applied in routine practice settings. Note: Pragmatic trials often find smaller effect sizes than explanatory trials but have higher external validity (generalizability to real-world populations) Additional sources: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3181997/
.
154.
Science/AAAS. Estimated annual cost of repeating failed experiments due to non-publication of results.
Science/AAAS https://www.science.org/content/article/study-claims-28-billion-year-spent-irreproducible-biomedical-research (2020)
Up to 50.0% of published preclinical research is irreproducible, with an estimated annual cost of $28 billion in the U.S. alone. This is based on $56B annual spending on preclinical research × 50.0% irreproducibility rate. Main causes: reagents/materials (36%), study design (28%), data analysis (25%), protocols (11%). Additional sources: https://www.science.org/content/article/study-claims-28-billion-year-spent-irreproducible-biomedical-research | https://www.idbs.com/2020/11/replicating-science-28-billion-is-wasted-every-year-in-the-us-alone/
.
